Linear table of data structure and algorithm (super detailed sequence table, linked list)

Preface

Through the previous data structure and algorithm basic knowledge we know some concepts and importance of data structure, then we summarize the content related to the linear table today. Of course, I use my own understanding to share with everyone.

In fact, to be honest, many people may still be confused the difference and connection between 1609f9af809e54 linear table , sequence table , and linked list

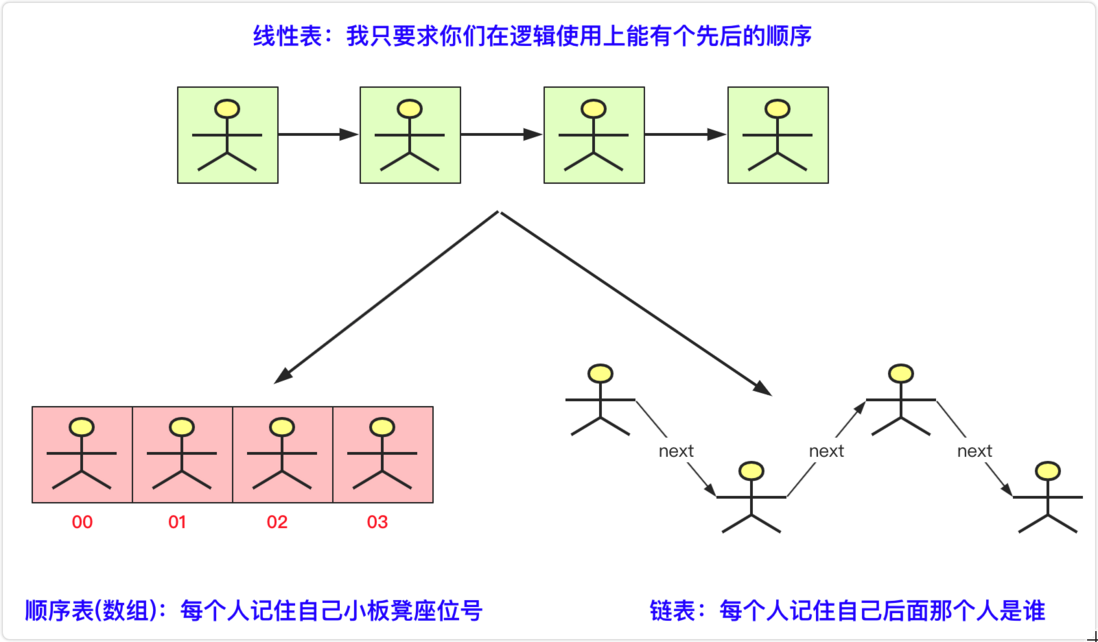
• Linear table: logical structure , which is the relationship between externally exposed data, and does not care about how the underlying layer is implemented. The logical structure of the data structure is broadly classified into linear structure and non-linear structure, while sequential tables and linked lists are all linear tables.
• Sequence table, linked list: physical structure , it is to realize a structure on the actual physical address of the structure. For example, the sequence table is implemented array The linked list uses pointer complete the main work. Different structures have different differences in different scenarios.

In Java, everyone knows the List interface type, which is the logical structure, because it encapsulates a series of methods and data in a linear relationship. The specific realization is actually related to the physical structure. For example, the content of the sequence table is stored using an array, and then a get, set, and add method must be based on the array , and the linked list is based on the pointer . When we consider the data relationship in the object, we must consider the properties of the pointer. Pointer's point and value.

Let's use a diagram to analyze the relationship of the linear table. It may be a little bit inaccurate, but it can be used for reference, and examples will be based on this figure later.

Basic structure of linear table

For a linear table. Regardless of its specific implementation, their method function names and implementation effects should be the same (that is, the use method is the same, the logical effect is the same, and the difference is operating efficiency). The concept of linear tables is somewhat similar to Java's interfaces/abstract classes. The most famous are List's Arraylist and LinkedList. List is a logical structure, which means that this structure is a linear list, while ArrayList and LinkedList are more of a physical structure (array and linked list).

Therefore, based on object-oriented programming thinking, we can write a linear table as an interface, and the specific implementation of the sequence table and linked list classes can implement the method of this linear table, improve the readability of the program, and one more important thing, remember When learning data structures and algorithms, the linear tables implemented are all fixed types (int). With the advancement of knowledge, we should use generics to achieve more reasonable. The specific design of the interface is as follows:

package LinerList;
public interface ListInterface<T> {    
    void Init(int initsize);//初始化表
    int length();
    boolean isEmpty();//是否为空
    int ElemIndex(T t);//找到编号
    T getElem(int index) throws Exception;//根据index获取数据
    void add(int index,T t) throws Exception;//根据index插入数据
    void delete(int index) throws Exception;
    void add(T t) throws Exception;//尾部插入
    void set(int index,T t) throws Exception;
    String toString();//转成String输出    
}

Sequence table

The sequence table is implemented based on arrays, so all implementations need to be based on array characteristics. For the structure of the sequence table, there should be an array of data and effective use length length .

Also need to pay attention to the size of the initialization array, you can fix the size, but the author will double if the memory is not enough for usability.

The following focuses on explaining some concepts and methods that are easy to confuse for beginners. Here the sequence table is compared to sitting on the bench.

Insert operation

add(int index,T t)

Where index is the numbered position of the insert, t is the inserted data, and the inserting process is:

(1) From the back (the last one has data bits) forward to the index and move one bit backward in turn to make room for the index position

(2) Assign the data to be inserted to the index position to complete the insert operation

It can be seen that if the sequence table is very long, if the insertion efficiency is relatively low in the first place (the insertion time complexity is O(n)), if the insertion is frequent, the complexity is quite high.

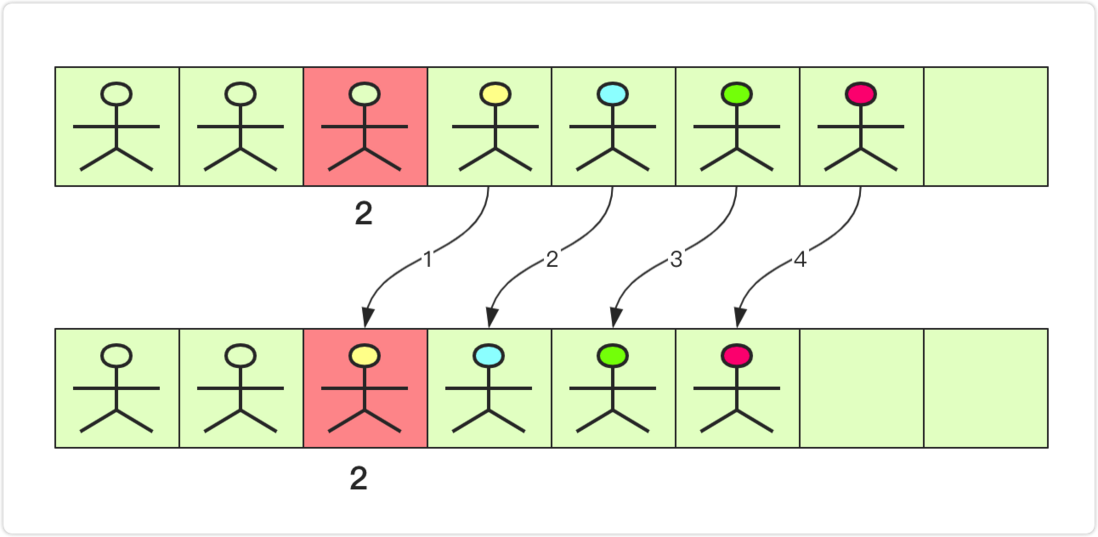
Delete operation

In the same way, deletion is very resource intensive. The principle is similar to inserting. The operation of deleting the index position is to assign data to the previous position sequentially from index+1. You can see this picture for details:

Code

Here I implement a sequence table for everyone to learn from:

package LinerList;

public class seqlist<T> implements ListInterface<T> {
    private Object[] date;//数组存放数据
    private int lenth;
    public seqlist() {//初始大小默认为10
        Init(10);
    }

    public void Init(int initsize) {//初始化
        this.date=new Object[initsize];
        lenth=0;        
    }
    public int length() {        
        return this.lenth;
    }

    public boolean isEmpty() {//是否为空
        if(this.lenth==0)
            return true;
        return false;
    }

    /*
     * * @param t    
     * 返回相等结果，为-1为false
     */
    public int ElemIndex(T t) {
        // TODO Auto-generated method stub
        for(int i=0;i<date.length;i++)
        {
            if(date[i].equals(t))
            {
                return i;
            }
        }
        return -1;
    }

    /*
     *获得第几个元素
     */
    public T getElem(int index) throws Exception {
        // TODO Auto-generated method stub
        if(index<0||index>lenth-1)
            throw new Exception("数值越界");
        return (T) date[index];
    }
    
    public void add(T t) throws Exception {//尾部插入
         add(lenth,t);
    }

    /*
     *根据编号插入
     */
    public void add(int index, T t) throws Exception {
        if(index<0||index>lenth)
            throw new Exception("数值越界");
        if (lenth==date.length)//扩容
        {
            Object newdate[]= new Object[lenth*2];
            for(int i=0;i<lenth;i++)
            {
                newdate[i]=date[i];
            }
            date=newdate;
        }
        for(int i=lenth-1;i>=index;i--)//后面元素后移动
        {
            date[i+1]=date[i];
        }
        date[index]=t;//插入元素
        lenth++;//顺序表长度+1
        
    }

    public void delete(int index) throws Exception {
        if(index<0||index>lenth-1)
            throw new Exception("数值越界");
        for(int i=index;i<lenth;i++)//index之后元素前移动
        {
            date[i]=date[i+1];
        }
        lenth--;//长度-1    
    }

    @Override
    public void set(int index, T t) throws Exception {
        if(index<0||index>lenth-1)
            throw new Exception("数值越界");
        date[index]=t;
    }
    public String  toString() {
        String vaString="";
        for(int i=0;i<lenth;i++)
        {
            vaString+=date[i].toString()+" ";
        }
        return vaString;
        
    }
}

Linked list

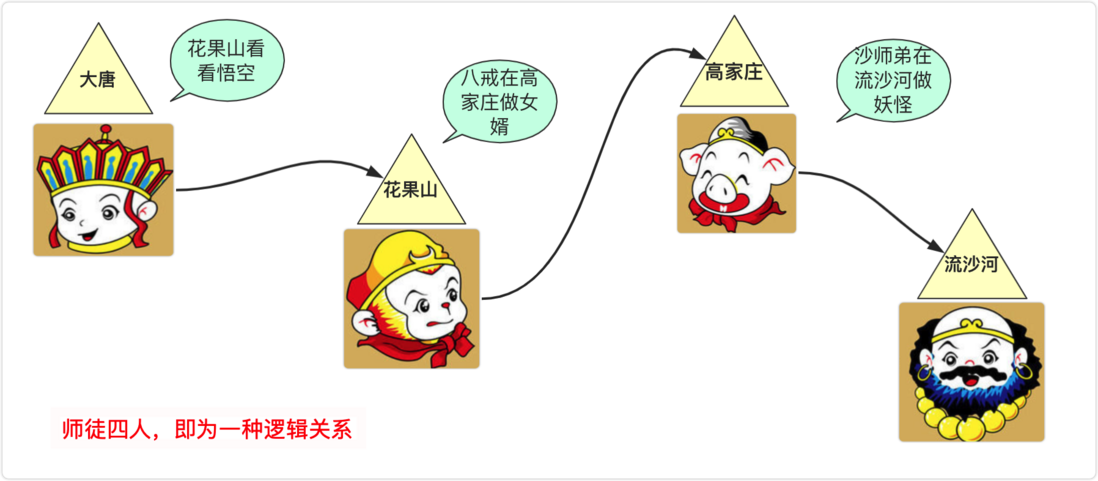
When learning c/c++, the linked list should be something that many people feel very convoluted. The big reason may be pointers. Although Java does not directly use pointers, we also need to understand the principle and application of pointers. A linked list is different from a sequential list (array). Its structure is linked into a linear structure like a chain, and each node in the linked list has a different address. You can understand that the linked list stores the address pointing to the node (area). The corresponding node can be found through this pointer.

For the physical storage structure, the relationship between addresses cannot be changed, and adjacent is adjacent. But for chain storage, the next address is actively recorded by the , which can be changed. This is like a brother who has been a brother of the same surname from birth, and our best friend may undergo some changes due to the phases of growth!

Just like the monks Tang, Wukong, Bajie, and Sha who learn from the Western Heaven. They had no connection, but they became brothers and apprentices. If you ask Wukong his master, he will immediately think of Tang Seng, because of the agreement under the Five Fingers Mountain.

basic structure

For linear tables, we only need a data array and length to represent basic information. For the linked list, we need a node (head node), and length respectively represent the stored node data and the length of the linked list. This node has data field and pointer field . The data field is to store real data, and the pointer field is to store the pointer of the next node. Its specific structure is:

class node<T>{
    T data;//节点的结果
    node next;//下一个连接的节点
    public node(){}
    public node(T data)
    {
        this.data=data;
    }
    public node(T data, node next) {
        this.data = data;
        this.next = next;
    } 
}

Leading node linked list VS without leading node linked list

Many people will not be clear about the difference between a leading node and a non-leading node linked list, or even understand what is a leading node and a non-leading node. Let me explain to you:

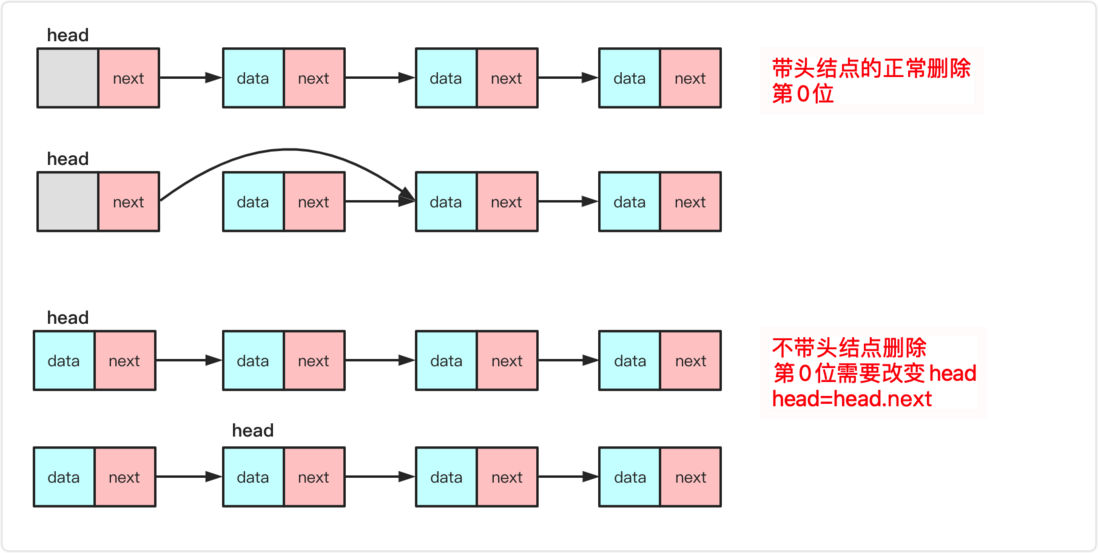
take the lead node : the head pointer always points to a node, this node does not store the effective value but only serves as an identification (equivalent to the head teacher with students)

does not take the lead node : The head pointer always points to the first valid node, and this node stores the valid value.

So what is the difference between a linked list with a lead node and a linked list without a lead node?

search on : There is no big difference, the lead node needs to be searched again.

: Insertion at the non-zeroth position makes little difference. After inserting the node without a head into the zeroth position, you need to change the direction of the head again.

delete the upper : the non-zeroth position deletes little difference, after deleting the zeroth position without a lead node, you need to change the head head point again.

Head deletion (lead node): The deletion of the lead node is the same as normal deletion. Directly head.next=head.next.next , so head.next directly points to the second element. The first one is deleted

Head deletion (no head node): The first node (head) without a head node stores valid data. It is also very simple to delete a node without a head, just point the head directly to the second node in the linked list. That is: head=head.next

In short: the lead node can make any node in the linked list be inserted and deleted equally through a fixed head. The linked list without a head node needs special processing when inserting or deleting the 0th position, and finally the head point must be changed. The is to insert and delete the first (especially insert). Of course, I suggest that you use the linked list much as possible when using the linked list in the avoid unnecessary troubles.

Lead pointer VS tail pointer

Basically, a linked list must have a head pointer, so what is the head and tail pointer?

head pointer: is the head node in the linked list, which becomes the head pointer.

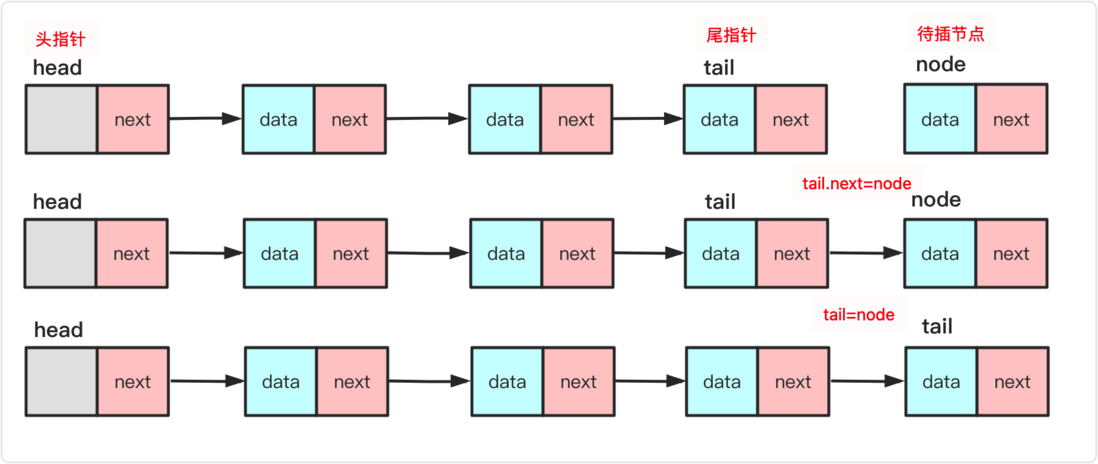
tail pointer: The tail pointer is a linked list with one more tail node. The advantage of the tail pointer is that the tail pointer can be inserted directly behind the tail pointer when inserting the tail, and then the order of the tail pointer can be changed.

However, if a singly linked list with a tail pointer deletes the tail, it is not efficient. You need to enumerate the entire linked list to find the node in front of the tail to delete.

Insert operation

add(int index,T t)
Where index is the numbered position of the insertion, and t is the inserted data. Inserting in any position in the linked list of the leading node is equivalent.
Join and insert a node node , and find the previous node inserted according to the index called pre . Then the operation process is

1. `node.next=pre.next`，将插入节点后面先与链表对应部分联系起来。此时node.next和pre.next一致。
2. `pre.next=node` 将node节点插入到链表中。

Of course, many times the linked list needs to be inserted at the end. If frequently inserted at the end and enumerated to the end each time, the efficiency may be low, and a tail pointer may be used to implement the tail insertion.

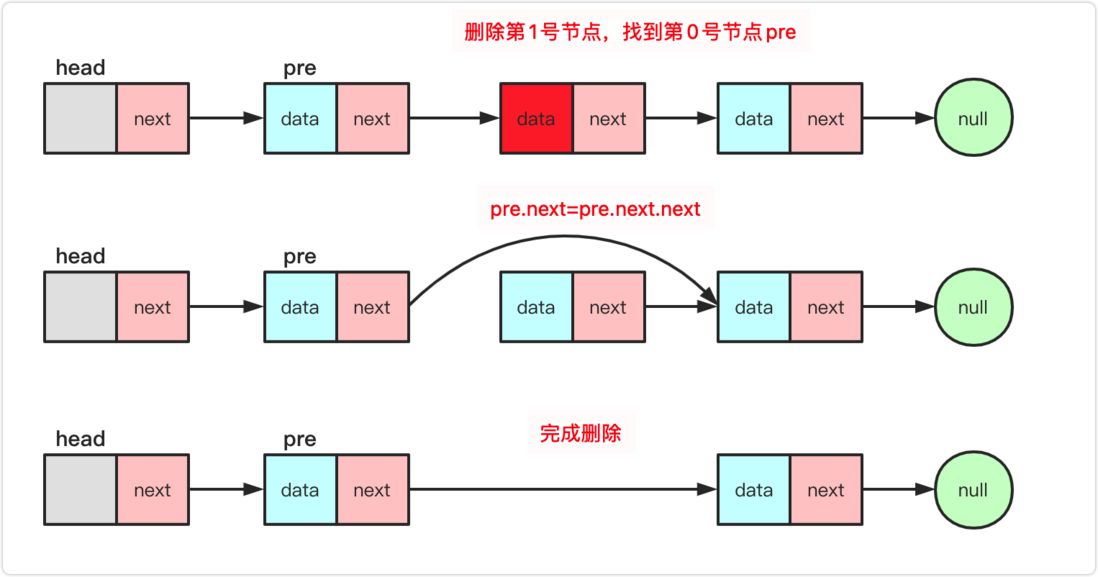
Delete operation

removed according to the index (mainly mastered) : delete(int index)

This method is a general method for the common linked list of the lead node (the same is true for deleting the tail), find the previous node pre of the index, pre.next=pre.next.next

Code

Here I also implement a singly linked list for your reference:

package LinerList;

class node<T>{
    T data;//节点的结果
    node next;//下一个连接的节点
    public node(){}
    public node(T data)
    {
        this.data=data;
    }
    public node(T data, node next) {
        this.data = data;
        this.next = next;
    }
   
}
public class Linkedlist<T> implements ListInterface<T>{

    node head;
    private int length;
    public Linkedlist() {
        head=new node();
        length=0;
    }
    public void Init(int initsize) {
        head.next=null;
        
    }

    public int length() {
        return this.length;
    }

    
    public boolean isEmpty() {
        if(length==0)return true;
        else return false;
    }

    /*
     * 获取元素编号
     */
    public int ElemIndex(T t) {
        node team=head.next;
        int index=0;
        while(team.next!=null)
        {
            if(team.data.equals(t))
            {
                return index;
            }
            index++;
            team=team.next;
        }
        return -1;//如果找不到
    }

    @Override
    public T getElem(int index) throws Exception {
        node team=head.next;
        if(index<0||index>length-1)
        {
            throw new Exception("数值越界");
        }
        for(int i=0;i<index;i++)
        {
            team=team.next;
        }
        return (T) team.data;
    }


    public void add(T t) throws Exception {
        add(length,t);
        
    }
    //带头节点的插入，第一个和最后一个一样操作
    public void add(int index, T value) throws Exception {
        if(index<0||index>length)
        {
            throw new Exception("数值越界");
        }
        node<T> team=head;//team 找到当前位置node
        for(int i=0;i<index;i++)
        {
             team=team.next;
        }
        node<T>node =new node(value);//新建一个node
        node.next=team.next;//指向index前位置的下一个指针
        team.next=node;//自己变成index位置    
        length++;
    }
    

    @Override
    public void delete(int index) throws Exception {
        if(index<0||index>length-1)
        {
            throw new Exception("数值越界");
        }
        node<T> team=head;//team 找到当前位置node
        for(int i=0;i<index;i++)//标记team 前一个节点
        {
             team=team.next;
        }
        //team.next节点就是我们要删除的节点
        team.next=team.next.next;
        length--;
    }

    @Override
    public void set(int index, T t) throws Exception {
        // TODO Auto-generated method stub
        if(index<0||index>length-1)
        {
            throw new Exception("数值越界");
        }
        node<T> team=head;//team 找到当前位置node
        for(int i=0;i<index;i++)
        {
             team=team.next;
        }
        team.data=t;//将数值赋值，其他不变
        
    }

    public String toString() {
        String va="";
        node team=head.next;
        while(team!=null)
        {
            va+=team.data+" ";
            team=team.next;
        }
        return va;
    }

}

to sum up

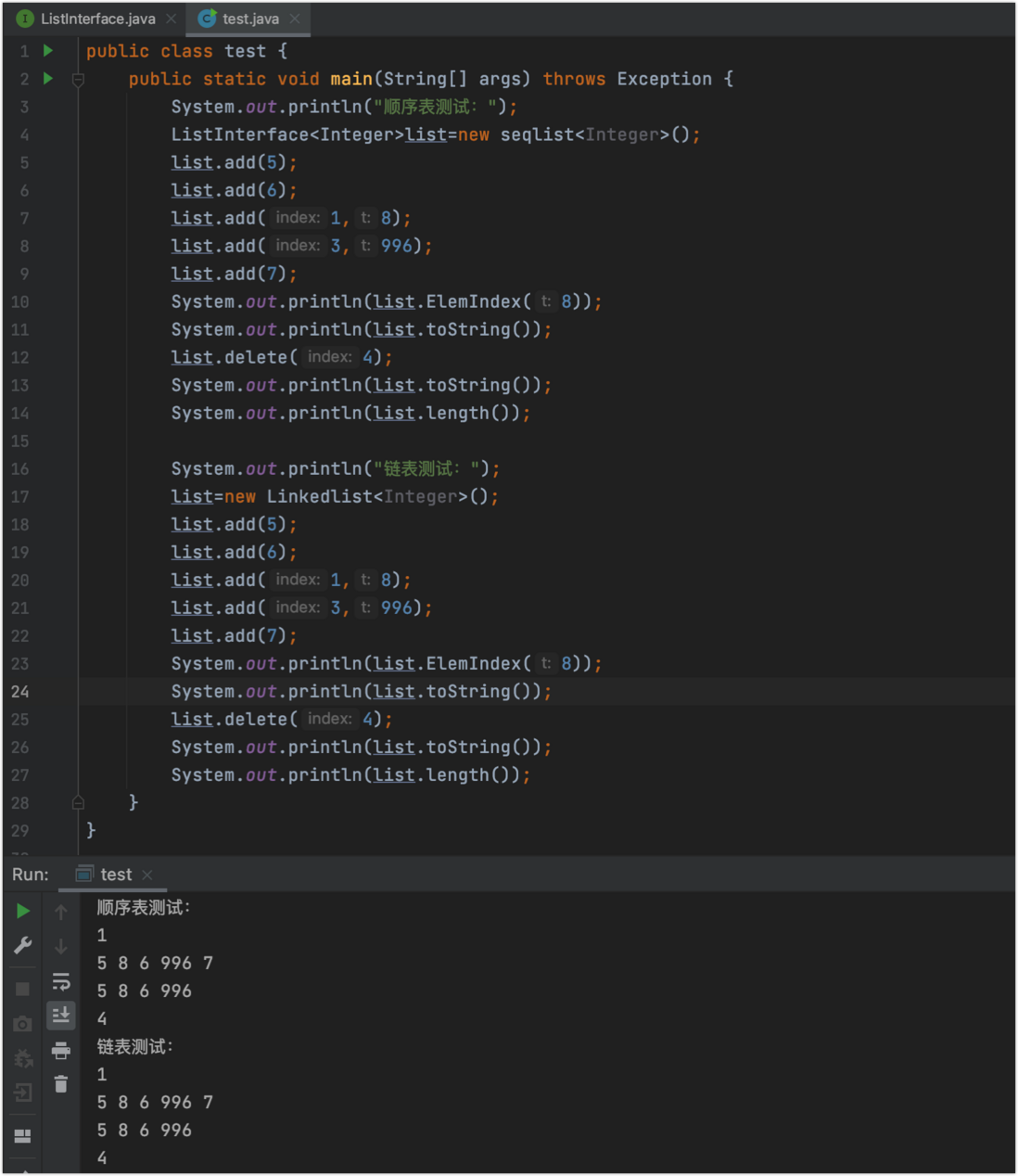
You may ask if this is correct, then let me test it:

Here is just a simple implementation, to achieve the basic method. Linked lists are only singly linked lists. The degree of sophistication can also be optimized. Limited capacity, if there is an error or optimization of local chiefs also requested correction .

The query speed of a singly linked list is slower because it needs to traverse from the beginning. If you insert at the end, you can consider designing a linked list with a tail pointer. The sequence table query speed may be fast but very time-consuming insertion, practical applications on demand selection !

Arraylist and LinkedList in Java are the representatives of the two methods, but LinkedList uses doubly linked list optimization, and JDK has also done a lot of optimization. So you don't need to make wheels, you can use them directly, but handwritten sequence tables and singly linked lists are still very valuable for learning.

If you understand the singly-linked list, the double-linked list is not far away (the next episode trailer)!

Original public number: bigsai
The article has been included in the data structure and algorithm learning warehouse that the whole network is paying attention to welcome star