Understand the full arrangement, combination, and subset issues in one article (collection is recommended)

Preface

Hello, everyone, I’m bigsai, long time no see! In the process of brushing questions and interviews, we often encounter some permutation and combination problems, and the problems of full permutation, combination, and subset are very classic problems. This article will take you to thoroughly understand the full array!

arrangement?

permutations and combinations of n elements (all elements) are .

seeking combination?

The combination is: all combinations (non-permutation) n elements and m elements.

subset?

The subset is: all the subsets of n elements ( all possible combinations ).

In general, the total number of permutations refers to all elements, and the difference is the order of arrangement; the combination is to select a fixed number of combinations (not looking at the permutation); the subset is to expand the combination, and all possible combinations (same or not) Consider permutation).

Of course, these three problems have similarities and slightly different ones. We may be exposed to more full permutations, so you can think of the combination and subset problems as an extension of the full permutation. And you may encounter problems pending character for duplicate situation. It is also very critical and important to adopt different strategies to remove duplication! There may be many specific methods for solving each problem. The most popular in total permutation is neighborhood swap method and backtracking method , while other combination and subset problems are classic backtracking problems. The most important and basic thing in this article is to master the non-repetitive full arrangement realized by these two methods. The others are based on this to transform and expand.

Permutation problem

The whole arrangement, the maximum total number of elements, is different ordered .

Full permutation without repetitive sequence

This question happens to . is the original question. You can go to a to try it after you finish your studies.

Problem Description:

Given a without repeating numbers, return all possible permutations.

Example:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

backtracking method to achieve full arrangement without repetition

The backtracking algorithm is used to solve the search problem, and the full arrangement is also a kind of search problem. Let’s review what a backtracking algorithm is:

The backtracking algorithm is actually a search trial process similar to enumeration, which is mainly to find the solution of the problem during the search trial process. When it is found that the solution condition is not met, it will "backtrack" and return and try another path.

And the full array just can use the heuristic method to enumerate all the possibilities. A sequence or set of length n. n！ kinds of possibilities for all its permutations and combinations. The specific heuristic strategy is as follows:

1. Select the first element from the set to be selected (a total of n cases), and mark that the element has been used and cannot be used anymore.
2. Recurse to the next layer on the basis of step 1, find and mark an element from the remaining n-1 elements according to the method of 1, and continue to recurse downward.
3. When all the elements are marked, the marked elements are sequentially collected and stored in the result. The current layer recursively ends and returns to the previous layer (at the same time, the marked elements of the current layer are cleared). This has been executed to the end.

If the backtracking process is roughly like this from the pseudo-code process:

递归函数：
  如果集合所有元素被标记：
      将临时储存添加到结果集中
  否则：
      从集合中未标记的元素中选取一个存储到临时集合中
      标记该元素被使用
      下一层递归函数
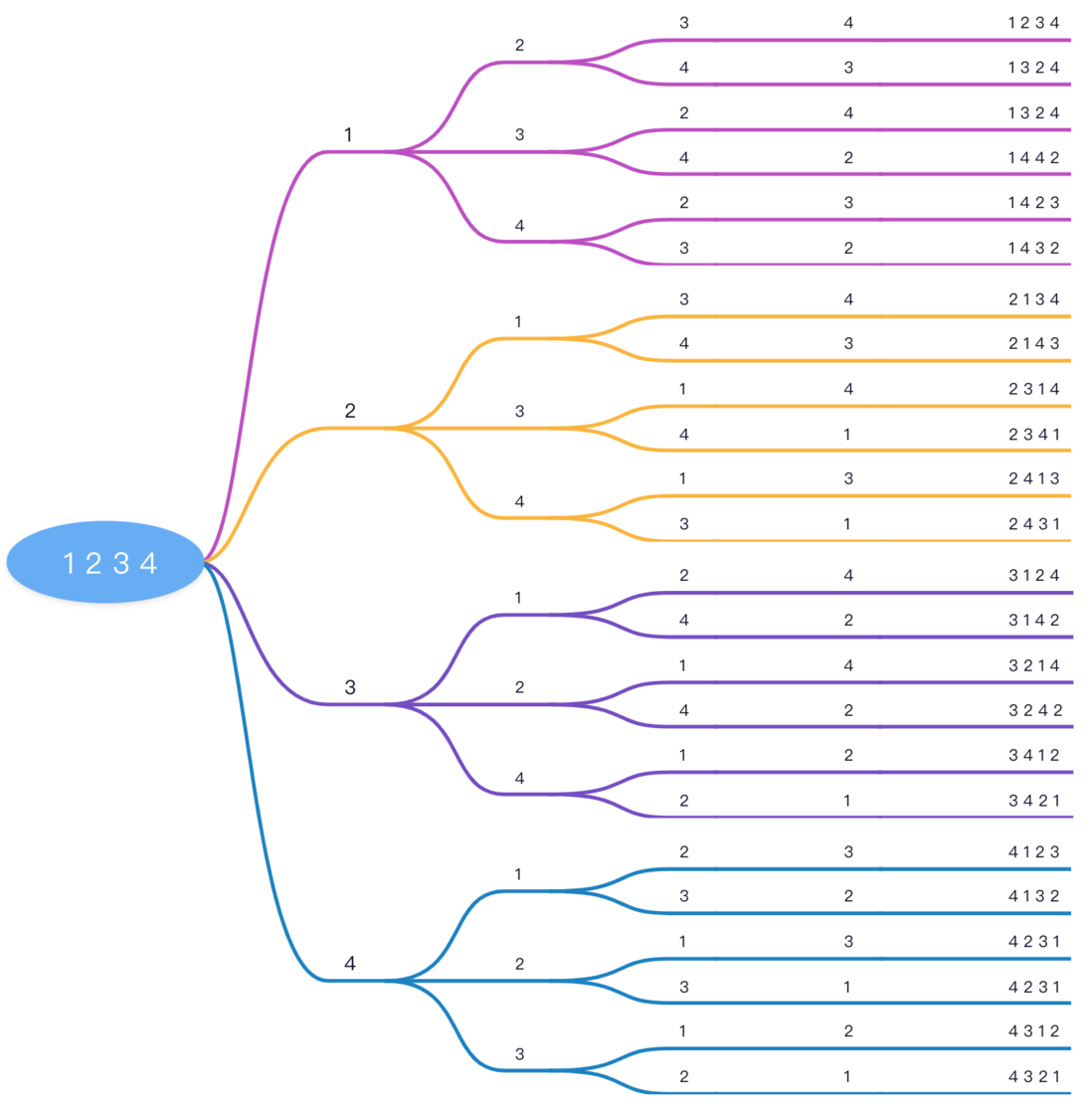
      (这层递归结束)标记该元素未被使用

If you use the sequence 1 2 3 4 to represent such a backtracking process, you can use this picture to show:

There are many ideas to implement with code. It is necessary to need a List to store temporary results, but we also have two processing ideas for the original collection. The first is to use List to store the collection, and then remove it after use. Recurse the next layer and add to the original position after the recursion is complete. Another way of thinking is to use a fixed array for storage, and use a boolean array to mark the corresponding position after using the corresponding position, and then restore it after the recursion ends. Because List frequently finds, inserts, deletes, and the efficiency is generally low, we generally to mark whether the element at that position is used .

The specific implementation code is:

List<List<Integer>> list;
public List<List<Integer>> permuteUnique(int[] nums) {
    list=new ArrayList<List<Integer>>();//最终的结果
    List<Integer> team=new ArrayList<Integer>();//回溯过程收集元素
    boolean jud[]=new boolean[nums.length];//用来标记
    dfs(jud, nums, team, 0);
    return list;
}
private  void dfs(boolean[] jud, int[] nums, List<Integer> team, int index) {
    int len = nums.length;
    if (index == len)// 停止
    {
        list.add(new ArrayList<Integer>(team));
    } else
        for (int i = 0; i < len; i++) {
            if (jud[i]) //当前数字被用过 当前即不可用
                continue;
            team.add(nums[i]);
            jud[i]=true;//标记该元素被使用
            dfs(jud, nums, team, index + 1);
            jud[i] = false;// 还原
            team.remove(index);//将结果移除临时集合
        }
}

Modify the output result to be consistent with the above mind map:

Neighborhood swap method to achieve full arrangement without repetition

The backtracking test is tentative filling, which considers and assigns each position individually. Although the neighborhood exchange method is also implemented recursively, it is a strategy and idea based on exchange. It is also very simple to understand. The idea of neighborhood exchange is to consider from left to right.

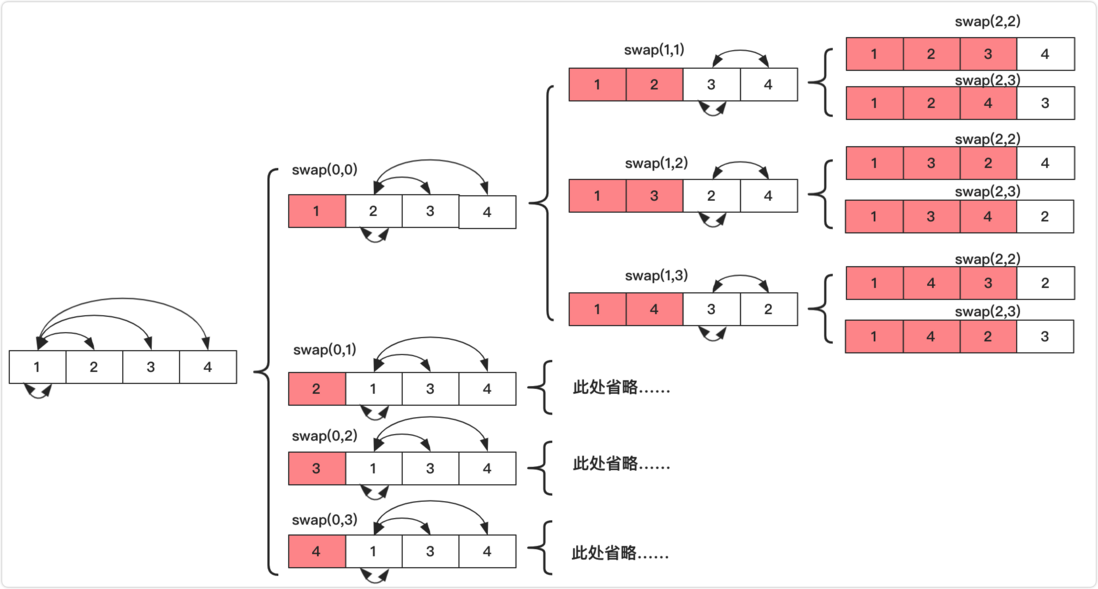
Because the sequence is not repeated, we start to divide the array into two parts: temporarily determined part and undefined part . At the beginning, it was the undetermined part. What we need to handle properly is the undetermined part. In the sequence of the undetermined part, we need to let every undetermined part have a chance to be in the undetermined first position, so the first element of the undetermined part must be exchanged with each (including oneself ), after the exchange is completed, go down to recursively solve other possibilities, after the solution is completed, exchange back (restore) and exchange with the latter. In this way, when the recursion reaches the last level, the value of the array is added to the result set. If you don’t understand, you can refer to the figure below for understanding:

The implementation code is:

class Solution {
     public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>>list=new ArrayList<List<Integer>>();
        arrange(nums,0,nums.length-1,list);
        return list;
     }

    private void arrange(int[] nums, int start, int end, List<List<Integer>> list) {
          if(start==end)//到最后一个 添加到结果中
          {
              List<Integer>list2=new ArrayList<Integer>();
              for(int a:nums)
              {
                  list2.add(a);
              }
              list.add(list2);
          }
          for(int i=start;i<=end;i++)//未确定部分开始交换
          {
              swap(nums,i,start);
              arrange(nums, start+1, end, list);
              swap(nums, i, start);//还原
          }
        
    }
    private void swap(int[] nums, int i, int j) {
        int team=nums[i];
        nums[i]=nums[j];
        nums[j]=team;
    }
}

So what’s the difference between the neighborhood swap and the total permutation of the backtracking solution? First, if the total permutation obtained by the backtracking method is in order, the result is lexicographically ordered, because the strategy is to fill, first small and then large, and Neighborhood interchange does not have this feature. Secondly, the efficiency of neighborhood swap in this case is higher than that of the backtracking algorithm. Although the magnitude is similar, the backtracking algorithm needs to maintain a set of frequent additions and deletions, etc., occupying a certain amount of resources.

Full permutation with repetitive sequence

There is a repetition corresponding to force buckle item 47 , the title is described as:

nums that can contain repeated numbers returns all non-repeated full permutations in any order.

Example 1:

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

Example 2:

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

prompt:

1 <= nums.length <= 8
-10 <= nums[i] <= 10

This is slightly different from the non-repeated full array above. This input array may contain repeated sequences. How we adopt appropriate strategies to repeat is crucial. We also analyze the two methods of backtracking and neighborhood interchange.

Retrospective pruning method
Because the complete backtracking is slower than direct recursion, the backtracking algorithm was not considered at the beginning, but the backtracking pruning method is better than the recursive neighborhood swap method. For the method that does not use hash deduplication, first perform sorting pre-ordering. There is no suspense in the processing, and the key to the backtracking method is to avoid repetition of the same numbers due to relative order problems. Therefore, the must not change when using the same number. The specific pruning rules are as follows:

• sort the sequence first

• Place the data tentatively at the current location

  • If the current position number has been used, it cannot be used
  • If the current number is equal to the previous one but the previous one is not used, then the current number cannot be used and the previous number needs to be used.

The idea is very simple, and the realization is also very simple:

List<List<Integer>> list;
public List<List<Integer>> permuteUnique(int[] nums) {
    list=new ArrayList<List<Integer>>();
    List<Integer> team=new ArrayList<Integer>();
    boolean jud[]=new boolean[nums.length];
    Arrays.sort(nums);
    dfs(jud, nums, team, 0);
    return list;
}
private  void dfs(boolean[] jud, int[] nums, List<Integer> team, int index) {
    // TODO Auto-generated method stub
    int len = nums.length;
    if (index == len)// 停止
    {
        list.add(new ArrayList<Integer>(team));
    } else
        for (int i = 0; i < len; i++) {
            if (jud[i]||(i>0&&nums[i]==nums[i-1]&&!jud[i-1])) //当前数字被用过 或者前一个相等的还没用，当前即不可用
                continue;
              team.add(nums[i]);
              jud[i]=true;
              dfs(jud, nums, team, index + 1);
            jud[i] = false;// 还原
            team.remove(index);
        }
}

Neighborhood Exchange Method

When we perform recursive full permutation, the main consideration is to get rid of the repetitive situation. How to remove the repetition of the neighborhood exchange?

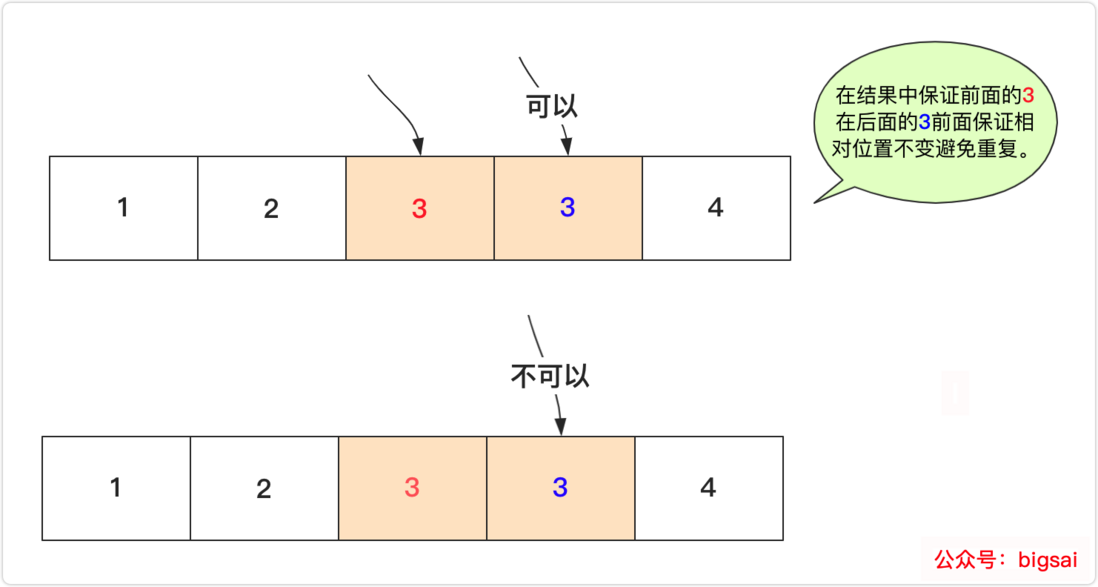
Use HashSet will not discuss this matter in this way, we exchange swap during the time of front to back, and then determine the front would not move, so we have to careful consideration and who exchange . For example, the first number of 1 1 2 3 has three cases instead of four cases (two 1 1 2 3 is a result) :

1 1 2 3 // 0 0 position swap
2 1 1 3 // 0 2 position swap
3 1 2 1 // 0 3 position swap

In addition, for example, 3 1 1 sequence, 3 exchanges with itself, and the following two 1s can only be exchanged with one of them, we can agree to exchange with the first one here, let’s look at a diagrammatic part of the process:

Therefore, when we start with an index, we must remember the following rules: exchange the same number only once (including the number whose value is equal to oneself). When judging whether the latter value appears, you can traverse or use hashSet(). Of course, the pain point of this method is that the efficiency of judging the latter number is low. So in the case of possible duplication, this method is generally efficient.

The specific implementation code is:

public List<List<Integer>> permuteUnique(int[] nums) {
         List<List<Integer>> list=new ArrayList<List<Integer>>();
         arrange(nums, 0, nums.length-1, list);
         return list;
     }

private void arrange(int[] nums, int start, int end, List<List<Integer>> list) {
      if(start==end)
      {
          List<Integer>list2=new ArrayList<Integer>();
          for(int a:nums)
          {
              list2.add(a);
          }
          list.add(list2);
      }
      Set<Integer>set=new HashSet<Integer>();      
      for(int i=start;i<=end;i++)
      {
          if(set.contains(nums[i]))
              continue;
             set.add(nums[i]);             
          swap(nums,i,start);
          arrange(nums, start+1, end, list);
          swap(nums, i, start);
      }    
}
private void swap(int[] nums, int i, int j) {
    int team=nums[i];
    nums[i]=nums[j];
    nums[j]=team;
}

Combination problem

The combined problem can be considered as a variant of the full permutation. The problem description ( force buckle 77 questions ):

Given two integers n and k, return all possible combinations of k numbers in 1...n.

Example:

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

analysis:

This problem is a classic retrospective problem. The combination needs to remember to only look at the elements and not the order of the elements. For example, a b and b a are the same combination. To avoid such repetition is the core , to avoid such repetition, it needs an int saving location of the currently selected element, traversed only select the next number after the indexing position, and the number of k, through a digital Type to record the number of processed numbers back to the current layer to control.

The specific implementation is also very easy. You need to create an array to store the corresponding number, and use the boolean array to determine whether the corresponding position number is used. Here, there is no need to store the number in the List. Finally, it is feasible to add the value to the result by judging the boolean array. The implementation code is:

class Solution { 
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> valueList=new ArrayList<List<Integer>>();//结果
        int num[]=new int[n];//数组存储1-n
        boolean jud[]=new boolean[n];//用于判断是否使用
        for(int i=0;i<n;i++)
        {
            num[i]=i+1;
        }
    
        List<Integer>team=new ArrayList<Integer>();
        dfs(num,-1,k,valueList,jud,n);
        return valueList;
    }
    private void dfs(int[] num,int index, int count,List<List<Integer>> valueList,boolean jud[],int n) {
        if(count==0)//k个元素满
        {
            List<Integer>list=new ArrayList<Integer>();
            for(int i=0;i<n;i++)
            {
                if (jud[i]) {
                    list.add(i+1);
                }
            }
            valueList.add(list);
        }
        else {
            for(int i=index+1;i<n;i++)//只能在index后遍历 回溯向下
            {
                jud[i]=true;
                dfs(num, i, count-1, valueList,jud,n);
                jud[i]=false;//还原
            
            }
        }    
    }
}

Subset

The subset problem is somewhat similar to the combination. Here are two cases of no repetition and repetition in the array.

Unrepeatable array subset

Problem description ( force button 78 questions ):

Give you an integer array nums, the elements in the array are different from each other. Return all possible subsets (power sets) of the array.

The solution set cannot contain duplicate subsets. You can return the solution set in any order.

Example 1:

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:

输入：nums = [0]
输出：[[],[0]]

prompt:

1 <= nums.length <= 10
-10 <= nums[i] <= 10
All elements in nums are different from each other

The subset is somewhat similar to the above combination. Of course, we don’t need to judge how many there are. We just need to follow the combined backtracking strategy recursively to the last , every time a recursive function is performed, it must be added to the result. (because the strategy adopted will not be repeated).

The implemented code is:

class Solution {
   public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> valueList=new ArrayList<List<Integer>>();
        boolean jud[]=new boolean[nums.length];
        List<Integer>team=new ArrayList<Integer>();
        dfs(nums,-1,valueList,jud);
        return valueList;
    }
    private void dfs(int[] num,int index,List<List<Integer>> valueList,boolean jud[]) {
        {//每进行递归函数都要加入到结果中
            List<Integer>list=new ArrayList<Integer>();
            for(int i=0;i<num.length;i++)
            {
                if (jud[i]) {
                    list.add(num[i]);
                }
            }
            valueList.add(list);
        }
        {
            for(int i=index+1;i<num.length;i++)
            {
                jud[i]=true;
                dfs(num, i, valueList,jud);
                jud[i]=false;
            
            }
        }
    }
}

There are duplicate array subsets

Title description ( 90 questions ):

Given an integer array nums that may contain repeated elements, return all possible subsets (power sets) of the array.

Note: The solution set cannot contain duplicate subsets.

Example:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

The difference from the above non-repeated array is that there may be repeated elements . We need to filter out duplicate elements in the results.

First of all, the subset problem is undoubtedly the use of the backtracking method to obtain the result. First, if the sequence is not repeated, we will use a boolean[] array mark the used elements and index indicate the current subscript, in progress When backtracking, we only recurse backward and set the enumerated element boolean[index] to true (restore when we come back). Each recursive collection of true elements in the boolean[] array is one of the subsets.

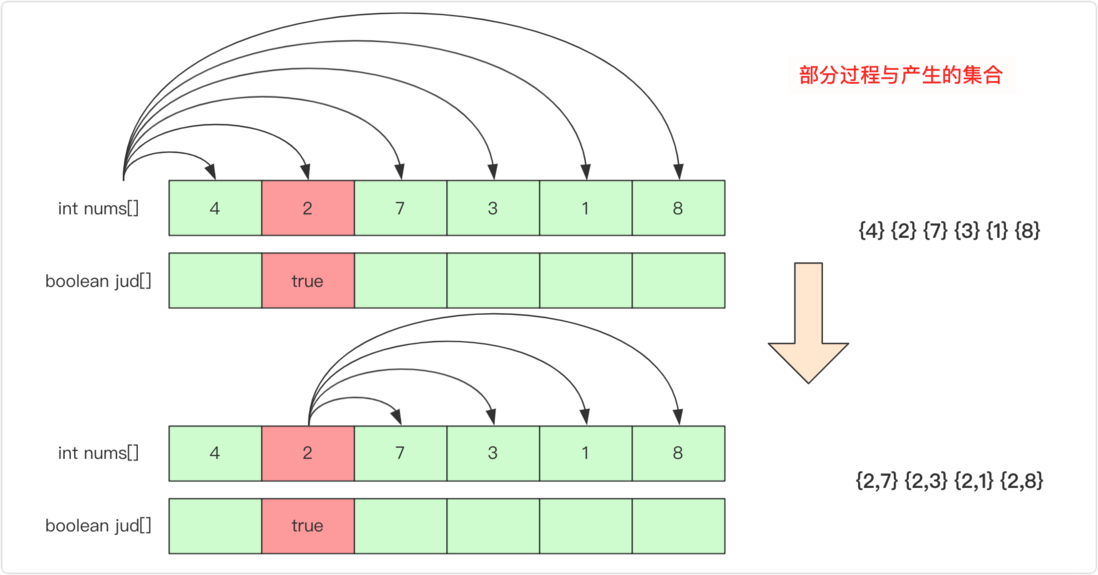
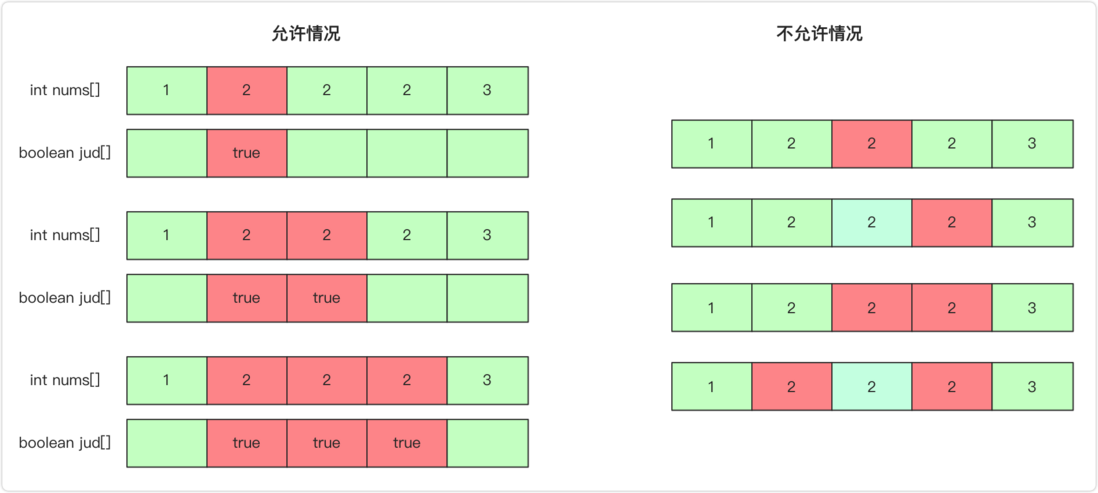
The processing of repeated elements is very similar to the processing of the previous full arrangement. The first is sorted first , and then the same element is only allowed to be used continuously from the first place when the recursive processing is carried out, but not skipped. Therefore, when recursively down, you need to determine whether the conditions are met ( first element or different from the previous one, or and the previous one has used ). For details, refer to this picture:

The implementation code is:

class Solution {
  public List<List<Integer>> subsetsWithDup(int[] nums) {
    Arrays.sort(nums);
    boolean jud[]=new boolean[nums.length];
    List<List<Integer>> valueList=new ArrayList<List<Integer>>();
    dfs(nums,-1,valueList,jud);
    return valueList;
  }

    private void dfs(int[] nums, int index, List<List<Integer>> valueList, boolean[] jud)   {
        // TODO Auto-generated method stub
        List<Integer>list=new ArrayList<Integer>();
        for(int i=0;i<nums.length;i++)
        {
            if (jud[i]) {
               list.add(nums[i]);
            }
        }
        valueList.add(list);
        for(int i=index+1;i<nums.length;i++)
        {//第一个元素 或 当前元素不和前面相同  或者相同且前面被使用了可以继续进行
            if((i==0)||(nums[i]!=nums[i-1])||(i>0&&jud[i-1]&&nums[i]==nums[i-1]))
            {
                jud[i]=true;
                dfs(nums, i, valueList,jud);
                jud[i]=false;
            }
        }
    }
}

Concluding remarks

So far, the whole permutation, combination, and subset issues of this article will be introduced here. Pay special attention to the ideas and strategies of problem handling and de-duplication. Of course, there are many problems similar to this, and you can master it with one more brush. Stay tuned later!

See you next time! Welcome to follow and like!

A search on WeChat: [bigsai] Get more knowledge about liver products
Ten miles of spring breeze, thank you