Cryptography series: blowfish symmetric key grouping algorithm

Introduction

Blowfish is a symmetric key block encryption algorithm invented by Bruce Schneier in 1993. Similar DES and AES are block encryption algorithms. Blowfish is used to replace the DES algorithm, and Blowfish has no commercial restrictions, anyone can Free to use.

In contrast, although AES is also a symmetric cryptographic algorithm with high cryptographic strength, if commercial use is required, an authorization fee must be paid to NIST.

Detailed blowfish

Like DES, blowfish uses the feistel cipher for block encryption. The block size of blowfish is 64 bits, and the variable key length can range from 32 bits to 448 bits.

Blowfish needs to perform 16 rounds of feistel encryption operation. Let's first get a rough experience of the encryption process of the blowfish algorithm from the following figure:

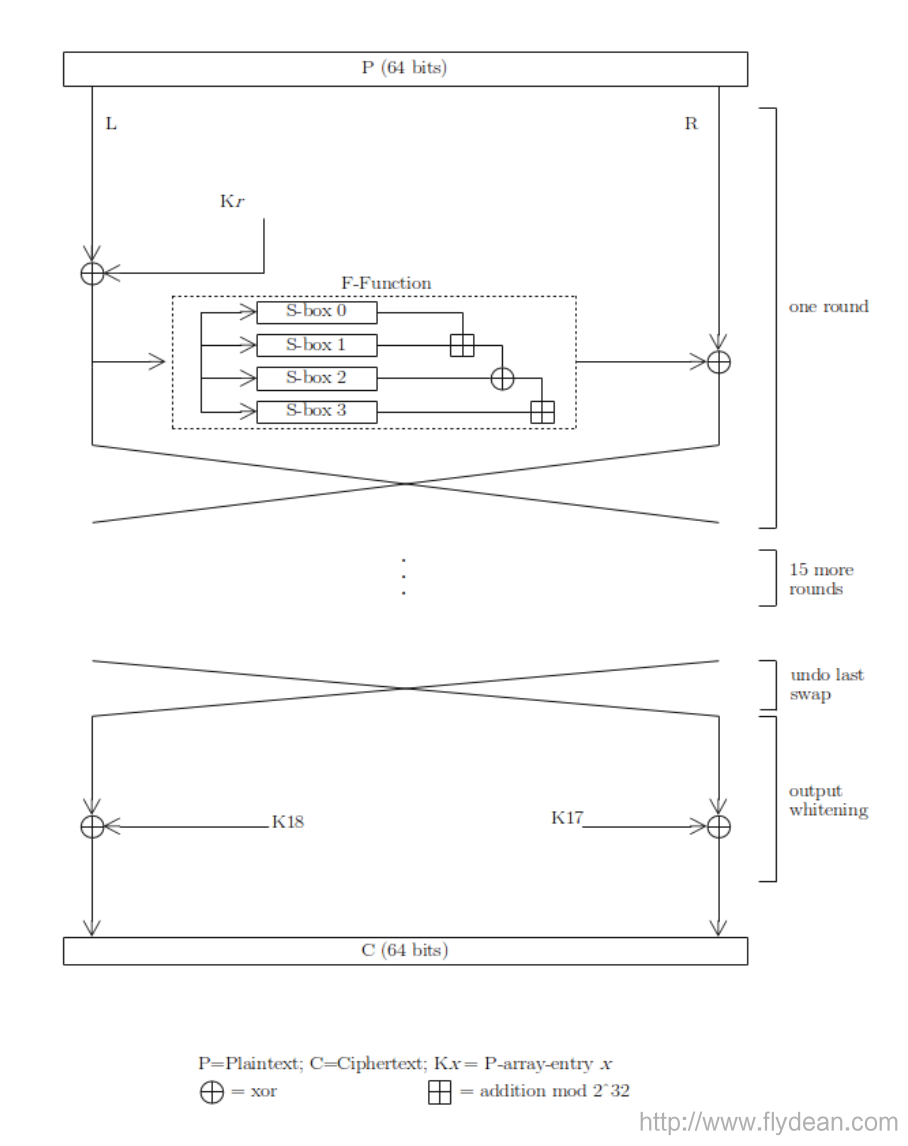
The general process is to divide P (raw data) into left and right parts, first take the left part and K _r do an XOR operation, the result obtained calls the F function, and finally the output result of the F function and the right half are performed XOR operation.

Change the position of the left and right parts, continue this operation, a total of 16 rounds to get the final encryption result.

You can see that the two most important variables in the entire encryption process are K _r and the F function.

Next we will explain in detail.

Key array and S-box

Key array

From the figure we can see that the range of _{r 1} to K ₁₈ . There is an array of 18 keys in total. The length of each key is 32 bits.

Let's take a look at how the key array is generated.

First, we use random numbers to initialize the key array. How can we generate a sufficiently random 32-bit number?

A very common method is to use the decimal part of the constant π and convert it to 16 net value, as shown below:

K₁ = 0x76a301d3

K₂ = 0xbc452aef

...

K₁₈ = 0xd7acc4a5

Remember the variable key length of blowfish? It is from 32bits to 448bits, that is, from 1 to 14 32-bit numbers. We use P _i to represent, then there are a total of 14 variable keys ₁ to P ₁₄

Next we need to use K and P to operate to generate the final K array.

We use K ₁ and P ₁ for XOR operation, K ₂ and P ₂ for XOR operation until K ₁₄ and P ₁₄

Because P has only 14 values, and K has 18 values, we need to reuse the value of P, which is K ₁₅ and P ₁ for XOR, K ₁₆ and P ₂ XOR until K ₁₈ and P ₄ .

The value after the exclusive OR is used as the value of the new K array.

Now we have a new K array.

Note that this K array is not the final array, let's look at it next.

S-box

Before generating the final P array, we have to introduce a concept called S-box.

In cryptography, the full name of s-box is substitution-box, which is a replacement box that can replace the input with different outputs.

The S-box receives the input of n bits and then converts it into the output of m bits.

Here n and m can be different.

Let's look at an example of S-box in DES:

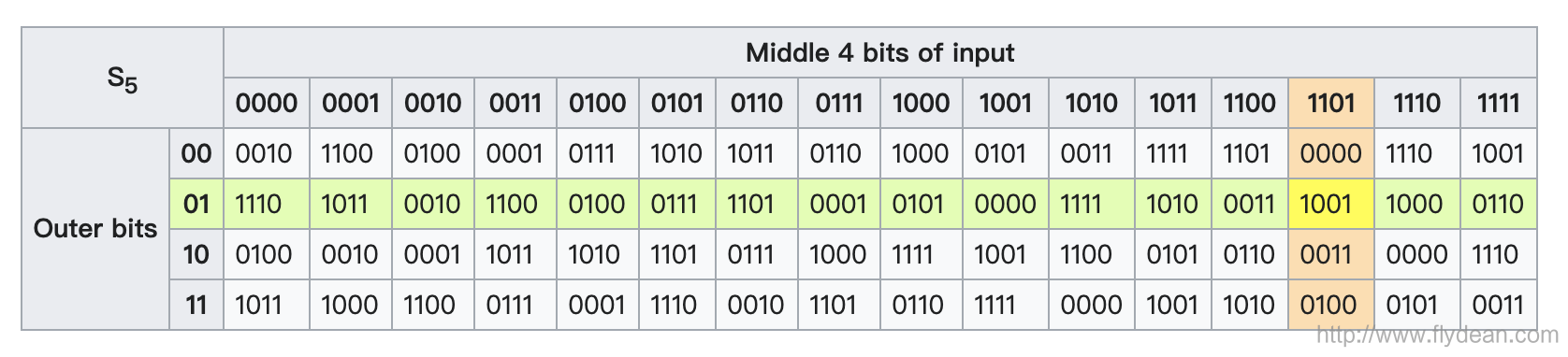
The above S-box converts 6-bits input into 4-bits output.

S-box can be fixed or dynamic. For example, S-box is static in DES, while S-box is dynamically generated in Blowfish and Twofish.

The F function in the Blowfish algorithm requires 4 S-boxes. The input of the F function is 32 bits. First, the 32 bits are divided into 4 parts, that is, 4 8 bits.

The function of S-box is to convert 8bits into 32bits.

Let's take a closer look at the workflow of the F function:

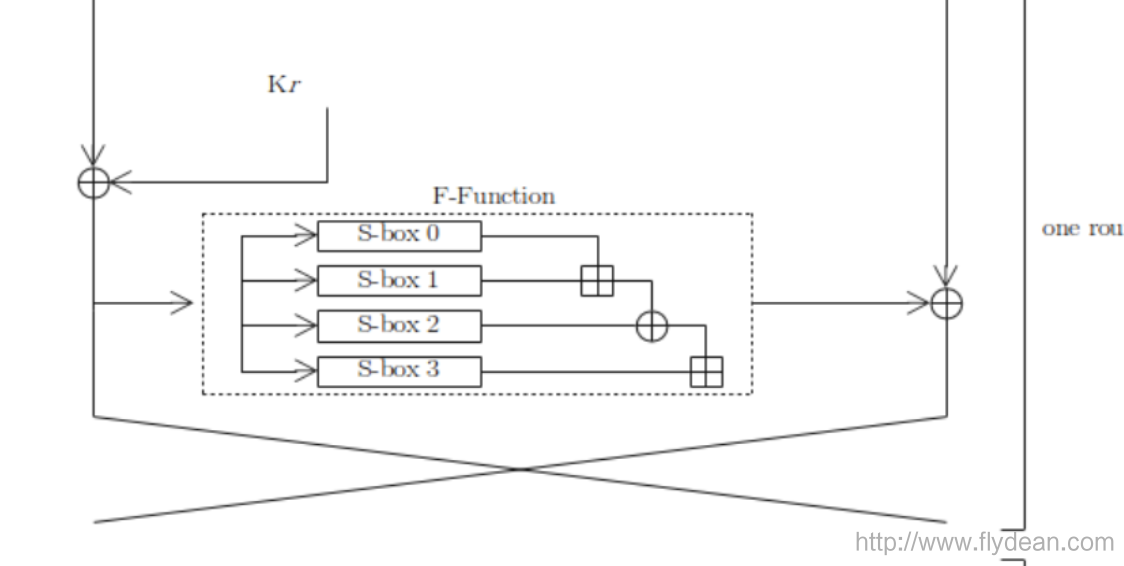
The values generated by the S-box will be added and then XORed. Finally get the final 32bits.

The initial value of the S-box can also be initialized with the decimal part of the constant π, just like the K array.

Generate the final K array

In the above two sections, we generated the initialized K array and S-box.

Blowfish believes that this is not safe enough and not random enough.

We also need to perform some operations to generate the final K array.

First, we take a 64bits with all 0s, then the K array and S-box, apply the blowfish algorithm to generate a 64bits.

_{this 64bits into two parts as the new K 160d538ad3678d 1} and K ₂ .

Then use this 64bits as input and call the blowfish algorithm again as the new K ₃ and K ₄ .

By analogy, all the elements in the K array are finally generated.

The array of 4 S-boxes is also generated according to the above process. So as to get the final S-box.

blowfish

With the final K array and S-box, we can actually encrypt the file to be encrypted.

Use a pseudo code to represent the entire process:

uint32_t P[18];
uint32_t S[4][256];

uint32_t f (uint32_t x) {
   uint32_t h = S[0][x >> 24] + S[1][x >> 16 & 0xff];
   return ( h ^ S[2][x >> 8 & 0xff] ) + S[3][x & 0xff];
}

void encrypt (uint32_t & L, uint32_t & R) {
   for (int i=0 ; i<16 ; i += 2) {
      L ^= P[i];
      R ^= f(L);
      R ^= P[i+1];
      L ^= f(R);
   }
   L ^= P[16];
   R ^= P[17];
   swap (L, R);
}

void decrypt (uint32_t & L, uint32_t & R) {
   for (int i=16 ; i > 0 ; i -= 2) {
      L ^= P[i+1];
      R ^= f(L);
      R ^= P[i];
      L ^= f(R);
   }
   L ^= P[1];
   R ^= P[0];
   swap (L, R);
}

  // ...
  // initializing the P-array and S-boxes with values derived from pi; omitted in the example
  // ...
{
   for (int i=0 ; i<18 ; ++i)
      P[i] ^= key[i % keylen];
   uint32_t L = 0, R = 0;
   for (int i=0 ; i<18 ; i+=2) {
      encrypt (L, R);
      P[i] = L; P[i+1] = R;
   }
   for (int i=0 ; i<4 ; ++i)
      for (int j=0 ; j<256; j+=2) {
         encrypt (L, R);
         S[i][j] = L; S[i][j+1] = R;
      }
}

Application of blowfish

As can be seen from the above process, it takes a certain amount of time for blowfish to generate the final K array and S-box, but once the generation is completed, or the key is unchanged, blowfish is still a very fast block encryption method .

Each new key requires about 4 KB of text preprocessing, which is very slow compared to other block cipher algorithms.

Is there any benefit to being slow?

Of course there is, because for a normal application, the key is not often changed. So the preprocessing will only be generated once. It will be very fast when used later.

For a malicious attacker, each time a new key is tried requires a long preprocessing, so it is very uneconomical for the attacker to crack the blowfish algorithm. So blowfish can resist dictionary attacks.

Because blowfish does not have any patent restrictions, anyone can use it for free. This benefit has promoted its popularity in cryptographic software.

For example, using blowfish's bcrypt algorithm, we will explain it in a later article.

Disadvantages of blowfish

Blowfish uses a 64-bit block size (compared to the 128-bit block size of AES) to make it vulnerable to birthday attacks, especially in environments like HTTPS. In 2016, the SWEET32 attack demonstrated how to use the birthday attack to perform plain text recovery (that is, decrypt ciphertext) on a 64-bit block size password.

Because the block of blowfish is only 64 bits, which is relatively small, the GnuPG project recommends not to use Blowfish to encrypt files larger than 4 GB.

In addition, if Blowfish only performs one round of encryption, it is vulnerable to known plaintext attacks with weak reflective keys. But our implementation uses 16 rounds of encryption, so it is not vulnerable to this kind of attack. But Bruce Schneier, the inventor of Blowfish, still recommends that you migrate to Twofish, the successor of Blowfish.

This article has been included in http://www.flydean.com/blowfish/

The most popular interpretation, the most profound dry goods, the most concise tutorial, and many tips you don't know are waiting for you to discover!

Welcome to pay attention to my official account: "Program those things", know technology, know you better!