The data structure of the stack is not just last-in, first-out?

What is a stack

Stacks encounter a lot in our daily coding. Many people's contact with stacks may only be limited to Recursively use stacks and StackOverflowException . The stack is a last-in, first-out data structure (you can imagine the biochemical pyramid The prison cell and the dog hole in the biochemical arena).

The stack is defined like this:

Stack (stack), also known as stack, is a linear table with operations limited and Limit the linear table that only inserts and deletes at the end of the table. This end is called the top of the stack, while the other end is called the bottom of the stack. Inserting a new element into a stack is also called pushing, pushing or pushing. It is to put the new element on top of the top element of the stack to make it a new top element; deleting an element from a stack is also called making a stack or Unstack, it is to delete the top element of the stack, so that the adjacent element becomes the new top element of the stack.

A little introduction to key terms:

operation is restricted : that is, you can't delete and insert arbitrarily in this table. It can only be inserted and deleted according to its rules. For example, the stack can only insert and delete at one end. Similarly, the queue is also limited in calculations and can only be operated at both ends.

linear table : The stack is also a linear table. The linear table was introduced in detail above. It expresses the logical relationship data. That is, the elements in the stack are adjacent. Of course, the specific implementation is also divided into arrays and linked lists, and their physical storage structures are different. But the logical structure (the purpose of realization) is the same.

stack top stack bottom: This description is biased towards logical content, because everyone knows that array is easier to insert and delete singly linked list is usually easier to So the end of the array can be the top of the stack, and the head of the linked list can be the top of the stack.

stack application: stack has a wide range of applications, such as your program execution to view the call stack, computer four arithmetic addition and subtraction operations, non-recursive forms of algorithms, bracket matching problems, and so on. So the stack is also a data structure that must be mastered. The simplest that everyone has experienced is that you take a book and stack it on top of each other, which is a last-in, first-out process. You can think of it as a stack. Below we introduce the stack implemented by the array linked list .

Array implementation

Stacks implemented by arrays are often used, and we often use arrays to implement a simple stack to solve simple problems.

Structural design

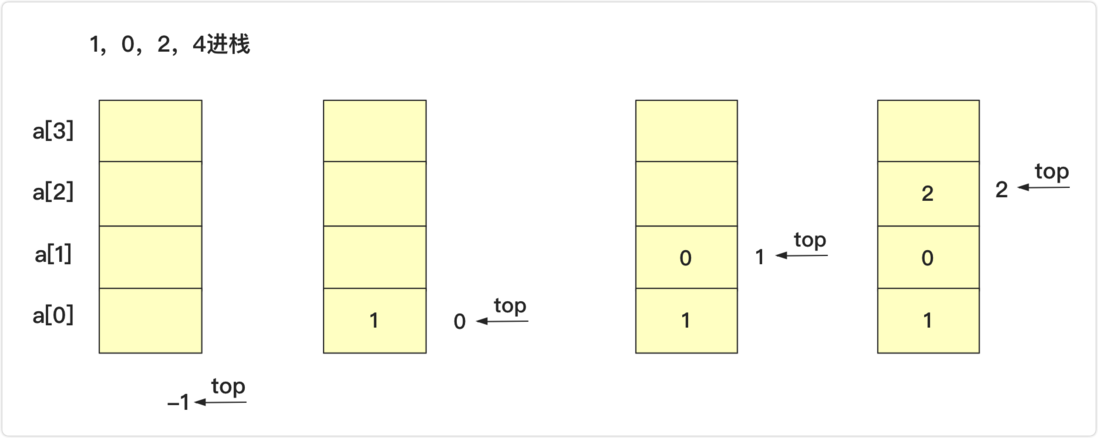
For arrays, our process of simulating the stack is very simple, because the stack is last in, first out, we can easily insert and delete at the end of the array. So we choose the end as the top of the stack. So the basic elements needed for a stack are a data[] array and a top (int) that represents the top position of the stack.

Then the initialization function code is:

private T data[];
private int top;
public seqStack() {
    data=(T[]) new Object[10];
    top=-1;
}
public seqStack(int maxsize)
{
    data=(T[]) new Object[maxsize];
    top=-1;
}

push insert

One of the core operations of the stack is push(): push operation.

• If top<array length-1. top++;a[top]=value; stack, 060d191906698d
• If top==array length-1; the stack is full.

pop pops up and returns to the top

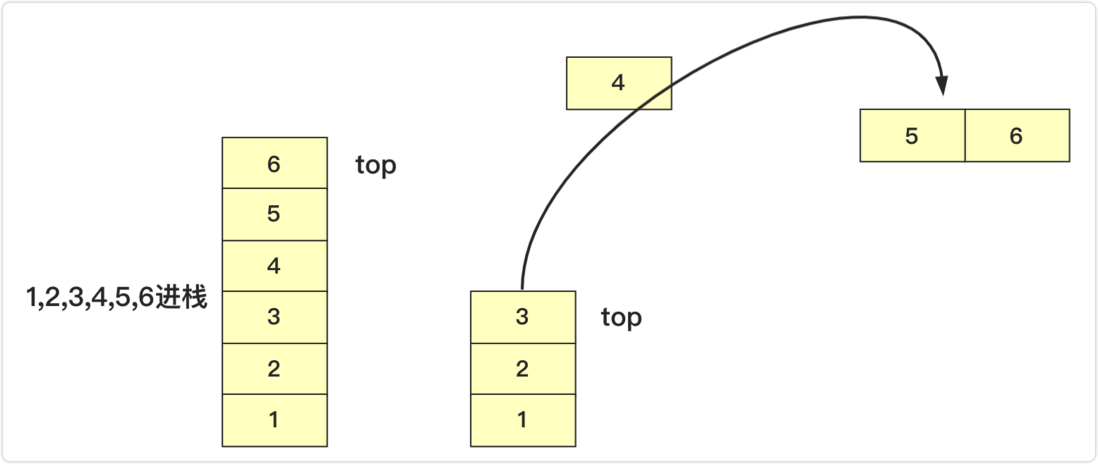
• If top>=0, the stack is not empty and can be popped. return data[top--];
• As shown in the figure below, the original stack is 1, 2, 3, 4, 5, 6 (top of the stack), perform a pop operation, top becomes 3 and returns 4;

Other operations

For example, when the peek operation returns to the top of the stack and does not pop up. So only need to meet the requirements of return data[top] .

array implementation:

package 队栈;

public class seqStack<T> {
    
    private T data[];
    private int top;
    public seqStack() {
        data=(T[]) new Object[10];
        top=-1;
    }
    public seqStack(int maxsize)
    {
        data=(T[]) new Object[maxsize];
        top=-1;
    }
    boolean isEmpty()
    {
        return top==-1;
    }
    int length()
    {
        return top+1;
    }
    
    boolean push(T value) throws Exception//压入栈
    {
        if(top+1>data.length-1)
        {
            throw new Exception("栈已满");
        }
        else {
            data[++top]=value;
            return true;
        }
    }
    T peek() throws Exception//返回栈顶元素不移除
    {
        if(!isEmpty())
        {
            return data[top];
        }
        else {
            throw new Exception("栈为空");
        }
    }
    T pop() throws Exception
    {
        if(isEmpty())
        {
            throw new Exception("栈为空");
        }
        else {
           return data[top--];
        }
    }
    public String toString()
    {
        if(top==-1)
        {
            return "";
        }
        else {
            String va="";
            for(int i=top;i>=0;i--)
            {
                va+=data[i]+"  ";
            }
            return va;
        }
    }
}

Linked list implementation

There is an array implementation, and a linked list can of course also be implemented. The design of the stack can be roughly divided into two ideas:

• at the end like an array. We all know that the list of low efficiency in the query, and the query to the tail of low efficiency, even with the tail pointer , can solve the tail insertion efficiency , but still not solve the deleted efficiency (delete need to find precursor node), also requires doubly linked list . Although the doubly linked list has been introduced in detail before, too complicated, !
• Therefore, we use the single-chain head as the top of the stack, insert directly after the head node, and delete the first node after the head node directly, so that it can be perfectly satisfied. The needs of the stack.

Structural design

The design is very similar to the linked list. To make a long story short, if you don't say a short story, you can understand the code directly.
linked list:

static class node<T>
{
    T data;
    node next;
    public node() {    
    }
    public node(T value)
    {
        this.data=value;
    }
}

basic structure:

public class lisStack <T>{
    int length;
    node<T> head;//头节点
    public lisStack() {
        head=new node<>();
        length=0;
    }
    //其他方法
}

push insert

same as the single-linked . If you don’t know much about it, you can look at the linear table written above for specific explanations.

There is a difference from the stack formed by the array. The stack realized by the chain has no limit on the size of the stack in theory (does not break through the memory system limit), and does not need to consider whether it is out of bounds, while the array needs to consider the capacity.

If a node team pushed onto the stack:

• Empty linked list into the stack head.next=team;
• Non-empty stack team.next=head.next;head.next=team;

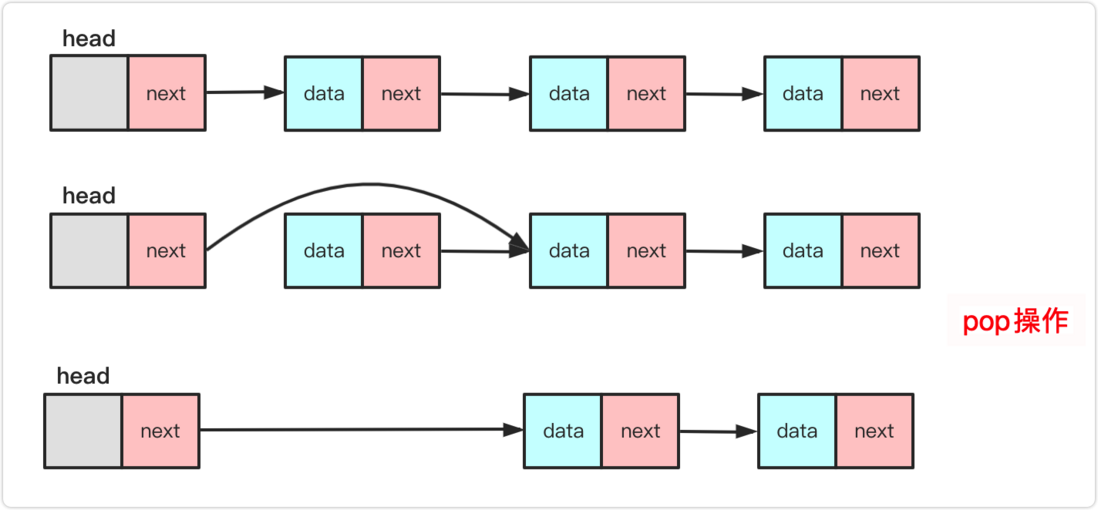
pop pop

same as the single-linked header deletion . If you don’t know much about it, please see the introduction of the author’s linear table first.

As with the array, it is necessary to determine whether the stack is empty. If the node team out of the stack: head points to the team rear-drive node.

Other operations

Others, such as returning to the top of the stack during peek operation, do not pop up. So only need to determine the empty to meet the meaning of the question return head.next.data . And length, you can traverse the linked list to return the length, or you can dynamically set (taken in this article) to follow the stack length change.

Linked list implementation:

package 队栈;

public class lisStack <T>{
    static class node<T>
    {
        T data;
        node next;
        public node() {    
        }
        public node(T value)
        {
            this.data=value;
        }
    }
    int length;
    node<T> head;//头节点
    public lisStack() {
        head=new node<>();
        length=0;
    }
    boolean isEmpty()
    {
        return head.next==null;
    }
    int length()
    {
        return length;
    }
    public void push(T value) {//近栈
       node<T> team=new node<T>(value);
       if(length==0)
       {
           head.next=team;
       }
       else {
        team.next=head.next;
        head.next=team;}
       length++;
    }
    public T peek() throws Exception {
        if(length==0) {throw new Exception("链表为空");}
        else {//删除
            return (T) head.next.data;
        }
  }
    public T pop() throws Exception {//出栈
      if(length==0) {throw new Exception("链表为空");}
      else {//删除
        T value=(T) head.next.data;
              head.next=head.next.next;//va.next
              length--;
              return value;
            }
    }
    public String toString(){
        if(length==0) {return "";}
        else {
              String va="";
            node team=head.next;
            while(team!=null)
            {
                va+=team.data+" ";
                team=team.next;
            }
            return va;
         }    
    }
}

Stack can play like this

Since the design stack is explained in detail above, here are two very classic and very classic examples of stacks (very high frequency, easy to forget, and very important, and we will not put common problems)

Leikou 20 valid brackets:

Question: Given a '('，')'，'{'，'}'，'['，']' , determine whether the string is valid.

A valid string must meet:

The left parenthesis must be closed with the same type of right parenthesis.
The opening parenthesis must be closed in the correct order.
Note that an empty string can be considered a valid string.

Example:

Input: "()[]{}"
Output: true

Example:

Input: "([)]"
Output: false

analysis:
The problem of brackets is a classic stack problem, so you must think of using the stack to deal with it. To judge whether a string is full or not a valid string, it depends on whether it can form a pair.

From a single bracket pair, (( and )) are not satisfied, only () can be satisfied, that is, one left and one right.

From multiple bracket pairs, the {[( string can also accept any infinite ( , [ , { . But if the parenthesis to the left can only receive the ) parenthesis (it becomes {[ ).

From the above, it can be seen as an idea of phase elimination. For example, (({[()()]})) string traversal can be processed like this:

• (({[( next ) eliminated to (({[
• (({[( next ) eliminated to (({[
• (({[ next ] eliminated to (({
• (({ next } eliminated to ((
• (( next ) eliminated to (
• ( next ) eliminated to so that it meets the meaning of the question

In each operation, it is judged whether the top bracket of the remaining valid brackets can be eliminated with the traversed. The process uses the stack to determine whether to add to the stack or eliminate the top . At the end, if the stack is empty, it means that it is satisfied, otherwise it is not satisfied. Of course, the specific brackets need to correspond, and the specific implementation code is:

public boolean isValid(String s) {
     Stack<Character>stack=new Stack<Character>();
     for(int i=0;i<s.length();i++)
     {    
         char te=s.charAt(i);
         if(te==']')
         {
             if(!stack.isEmpty()&&stack.pop()=='[')
                 continue;
             else {
                return false;
            }
         }
         else if(te=='}')
         {
             if(!stack.isEmpty()&&stack.pop()=='{')
                 continue;
             else {
                return false;
            }
         }
         else if(te==')')
         {
             if(!stack.isEmpty()&&stack.pop()=='(')
                 continue;
             else {
                return false;
             }
         }
         else
             stack.push(te);
     }
     return stack.isEmpty(); 
 }

Of course, the stack that comes with JDK is not fast to use, you can use array optimization:

public boolean isValid(String s) {
    char a[]=new char[s.length()];
    int index=-1;
     for(int i=0;i<s.length();i++)
     {    
         char te=s.charAt(i);
         if(te==']')
         {
             if(index>=0&&a[index]=='[')
                 index--;
             else {
                return false;
            }
         }
         else if(te=='}')
         {
             if(index>=0&&a[index]=='{')
                 index--;
             else {
                return false;
            }
         }
         else if(te==')')
         {
             if(index>=0&&a[index]=='(')
                 index--;
             else {
                return false;
             }
         }
         else
             a[++index]=te;
     }
     return index==-1; 
 }

Force buckle 32 longest effective bracket (difficult)

Title description: Given a string containing only'(' and')', find the length of the longest substring containing valid parentheses.

Example:

Input: "(()"
Output: 2
Explanation: The longest valid bracket substring is "()"

Example:

Input: ")()())"
Output: 4
Explanation: The longest valid bracket substring is "()()"

Scheme 1 Violence

The core idea of this question is to use the stack to simulate . This question is a bit simpler because there are only ( and ) . When using violence, you can loop to find the longest valid bracket each time. When the brackets are matched, can directly terminate . The situation is that ) right brackets that cannot be matched.

For example, ())( to the third one cannot be connected to the front. If you come to ( only need to expect ) to come later. A ) can form a pair with a ( ( in the stack.

Of course, in the specific implementation, we use an array to simulate the stack, and the implementation code is:

public  int longestValidParentheses(String s) {
    char str[]=s.toCharArray();//字符数组
    int max=0;
    for(int i=0;i<str.length-1;i++)
    {
        int index=-1;
        if(max>=str.length-i)
            break;
        for(int j=i;j<str.length;j++)
        {
            if(str[j]=='(')
                index++;
            else {
                if(index<0)
                {
                    i=j;
                    break;
                }
                else {
                    index--;
                }
            }
            if(index==-1&&(j-i+1>max))
            {
                max=j-i+1;
            }
        }
    }    
    return max;
}

This complexity is too high, let's see how to use stack optimization.

program two stack optimization

this problem from an O(n2) time complexity to O(n) ? It's easy, we need to pay attention to his process. Let's take a look at a few of the largest possible situations.

• ( ) ) ( ) ( ( ) ( ) ) largest part (separated by spaces)
• ( ) ( ) ( ( ( ) largest part of the front
• ( ( ( ( ( ( ) ( ) ( ) ( ) maximum is the back part

For such an acquisition, you will find that there are some differences between different brackets:
( : Once the left bracket appears, he expects a ) to match, but there may be ) after it and there are many other bracket pairs in the middle.
) : There are two situations for right expansion:

• One is that it is no longer possible to continue past the opening parenthesis. E.g. ( ) ) ( ) third bracket appears that the entire string has been impossible to continuously, maximum in either its left , or then its right . You can understand it as a clear initial mechanism.
• In another case, ) is that there is ( target stack that can be matched with it. matched, it should be added to the number of after elimination, and judge whether it is the maximum value. (Explained below)

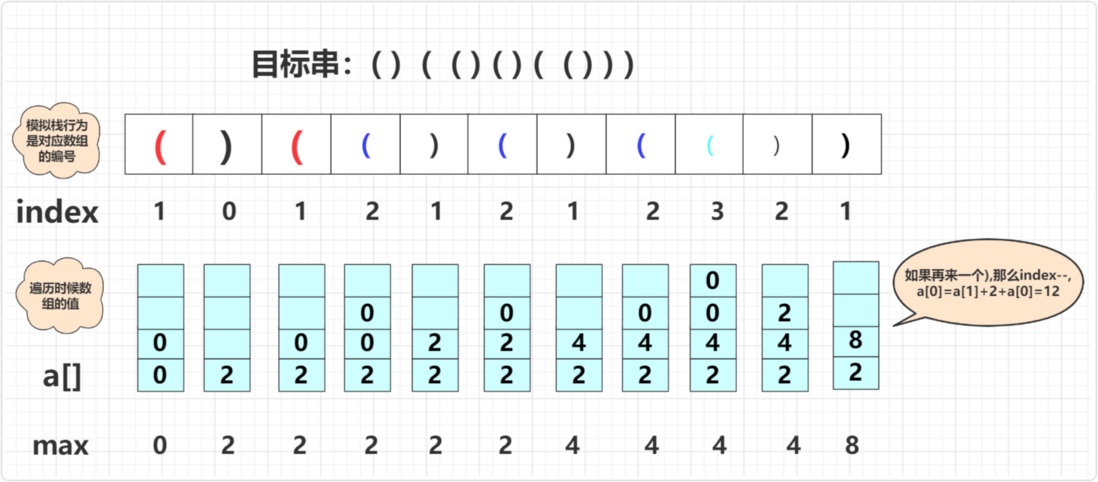
In is to use an int array to mark the current level (stack depth) with the correct number of parentheses. Simulate the stack behavior once from left to right, and when ) too much 060d19190676df (there is no ( in the current stack for matching), the data will be cleared and restarted. This goes to the end. You can think of it as a station connection. When you encounter ( you will go to a step and clear the new step . When you encounter ) you will go to the next step and add the to the descending step . Specifically, you can see the simulation process in the following picture:
( ) ( ( ) ( ) ( ( ) ) )

Take a closer look at this picture, the specific implementation code is:

 public static int longestValidParentheses(String s) {
        int max=0;    
        int value[]=new int[s.length()+1];
        int index=0;
        for(int i=0;i<s.length();i++)
        {
            if(s.charAt(i)=='(')
            {
                index++;
                value[index]=0;
            }
            else {//")"
                if(index==0)
                {
                    value[0]=0;
                }
                else {
                    value[index-1]+=value[index--]+2;//叠加
                    if(value[index]>max)//更新
                        max=value[index];
                }
            }
        }
        return max;
 }

The stack can also be used, but the efficiency is slightly lower than the array:

public int longestValidParentheses(String s) {
  int maxans = 0;
  Stack<Integer> stack = new Stack<>();
  stack.push(-1);
  for (int i = 0; i < s.length(); i++) {
    if (s.charAt(i) == '(') {//(将当前的 
      stack.push(i);
    } else {
      stack.pop();
      if (stack.empty()) {
        stack.push(i);
      } else {//i-stack.peek就是i是出现的总个数 peek是还没匹配的个数
        maxans = Math.max(maxans, i - stack.peek());
      }
    }
  }
  return maxans;
}

to sum up

At this point, the introduction to the stack in this article is over. I believe you can write a stack by hand and try to solve the bracket matching problem! Of course, there are still many problems that the stack can solve, such as rainwater problems, non-recursive traversal of binary trees, etc. Some important ones will be summarized.

Welcome to pay attention to my public bigsai learn knowledge first-hand, in the end, don't stingy with your one-click triple connection, original and ask for support, thank you !