The interviewer asked me to write the queue, almost didn't write it out

Preface

Stacks and queues are a good pair of brothers. We introduced an article about stacks (stacks, not just last in, first out). The mechanism of stacks is relatively simple. Last in, first out is like entering a small cave. There is only one cave. Entrance and exit can only be last in, first out (the ones who are outside go out first, and those who are blocked inside are a bit unlucky) . The queue is like a tunnel, the people behind follow the front, the people in front go out first (first in, first out) . Daily queuing is a description of the form of queue operation!

The stack is a data structure that loves the new and dislikes the old. When the new comes, the new will be processed and the old will be stopped here (we find people and appointments to do things the most annoying this kind of people). Queue is a kind of unselfish data structure, queuing First come first served, pay attention to order , so this data structure is widely used in programming, middleware, etc., such as message queues, FIFO disk scheduling, binary tree hierarchy traversal, BFS width first search and so on.

The core concept of the queue is: first in, first out!

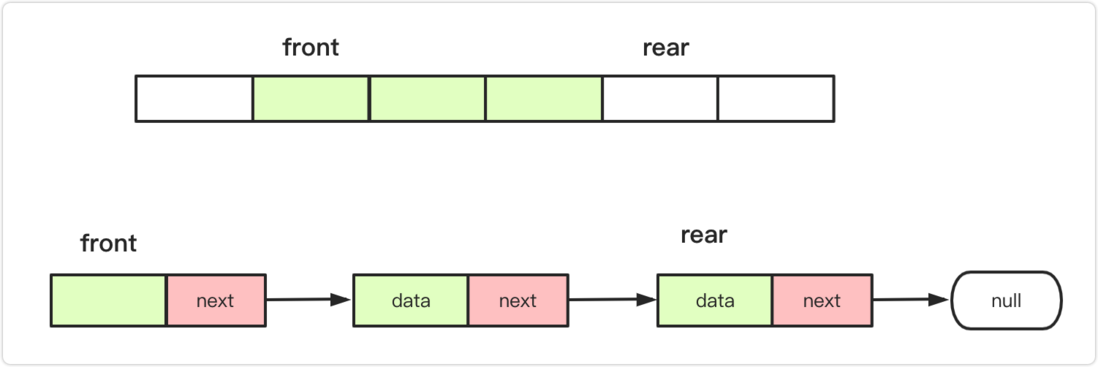
The concept of the queue : The queue is a special linear table. The special feature is that it only allows delete operations at the front of the table, and inserts at the rear of the table, just like the stack. A queue is a linear list with restricted operations. The end that performs the insertion operation is called the end of the team, and the end that performs the deletion operation is called the head of the team.

At the same time, read this article a good idea to understand basic operation sequence table and stack data structure ! Better learning effect!

Queue introduction

When we design the queue, we can choose a standard. Here we take to design the circular queue as the standard for queue design.

team head front: delete one end of the data.

tail rear: inserted into one end of the data.

For the array , it is easier to insert from the back of the array, and it is more difficult to insert in the front of the array. Therefore, the head of the queue that is generally implemented with an array is in front of the array, and the tail is behind the array; for the linked list , insert and delete are performed at the two ends separately. The most convenient option to delete the head (front) and insert the tail.

Implementation:

• MyCircularQueue(k): Constructor, set the queue length to k.
• Front: Get elements from the head of the team. If the queue is empty, -1 is returned.
• Rear: Get the tail element. If the queue is empty, -1 is returned.
• enQueue(value): Insert an element into the circular queue. It returns true if it is successfully inserted.
• deQueue(): Remove an element from the circular queue. It returns true if it is successfully deleted.
• isEmpty(): Check whether the circular queue is empty.
• isFull(): Check whether the circular queue is full.

Normal queue

According to the above introduction, it is easy for us to know how the array is implemented. Use array simulation to represent the queue. Consider initialization, insertion, and problems.

Some operations that need to be noted in this ordinary queue are:

initialize : the front and rear of the array point to 0. (When the front and rear subscripts are equal, the queue is empty)

Join the team: The team is dissatisfied, the array does not cross the boundary, the value is passed at the end of the team, and then the end of the team is subscript +1 (the rear of the team is actually one bit ahead, in order to distinguish the empty queue)

Departure: If the team is not empty, take the element of the head position first, and +1 at the head of the team.

But it is easy to find the problem , each space domain can only be used once, resulting in extremely waste of space, very easy to cross the boundary!

Circular queue (array implementation)

In response to the above problems. There is a better solution! It is the (array) memory reuse has been applied for This is what we call a circular queue. One advantage of circular queues is that we can use the previously used space of this queue. In a normal queue, once a queue is full, we cannot insert the next element, even if there is still room in front of the queue. But with circular queues, we can use these spaces to store new values.

The circular queue implemented by the array is logically modified Because we only need front and rear pointers in the queue. Rear is logically behind, front is logically in front, but in fact they are not necessarily who is in front and who is behind. When calculating the distance, you need to add the length of the array to subtract front, and then calculate the remainder. Can.

initializes : both front and rear of the array point to 0. What needs to be noted here is that when front and rear are in the same position, it proves that the queue is empty. In addition, when I implemented the actual implementation, I vacated the larger position of the array application to prevent the queue from being full and causing the front and rear to be in the same position.

the team : the team is dissatisfied, pass the value at the end of the team first, and then rear=(rear + 1) % maxsize;

out of the team : The team is not empty, first take the element of the head position, front=(front + 1)% maxsize;

Here, if the dequeue and enqueue indicators are added, if you need to turn to the head position at the end, you directly find the position by +1 to find the remainder (compared to judging whether it is at the end is more concise), where maxsize is the actual size of the array.

is empty : return rear == front;

Size : return (rear+maxsize-front)%maxsize; It is easy to understand here, a picture can explain clearly, whether it is the front and the back can meet the requirements.

There are a few things that everyone needs to pay attention to, that is, if the index is added, if you need to turn to the head at the end. It can be judged whether the end position of the array is reached. You can also directly +1 for the remainder. Among them, maxsize is the actual size of the array.

Implementation:

public class MyCircularQueue {
    private int data[];// 数组容器
    private int front;// 头
    private int rear;// 尾
    private int maxsize;// 最大长度
    public MyCircularQueue(int k) {
        data = new int[k+1];
        front = 0;
        rear = 0;
        maxsize = k+1;
    }

    public boolean enQueue(int value)  {
        if (isFull())
            return  false;
        else {
            data[rear] = value;
            rear=(rear + 1) % maxsize;
        }
        return  true;
    }

    public boolean deQueue() {
        if (isEmpty())
            return false;
        else {
            front=(front+1)%maxsize;
        }
        return  true;
    }

    public int Front() {
        if(isEmpty())
            return -1;
        return data[front];
    }

    public int Rear() {
        if(isEmpty())
            return -1;
        return data[(rear-1+maxsize)%maxsize];
    }

    public boolean isEmpty() {
        return rear == front;
    }

    public boolean isFull() {
        return (rear + 1) % maxsize == front;
    }
}

Circular queue (linked list implementation)

For the queue implemented by the linked list, the position of the head and tail should be considered according to the first-in first-out rule

We know that the queue is first-in-first-out. For linked lists, we can use singly linked lists as much as possible, which can be as convenient as possible, while also taking into account efficiency. There are probably two implementation schemes for using linked lists:

plan If the queue head is set at the end of the linked list, the queue tail is set at the head of the linked list. Then the team tail into the team insert into the head of the linked list is no problem, easy to achieve, but if the team head delete at the end of the linked list, if you do not set the tail pointer to traverse to the end of the team, but set the tail pointer to delete it needs to be removed The precursor node needs a doubly linked list , which is very troublesome.

plan two If the head of the queue is set at the head of the linked list, and the tail of the queue is set at the end of the linked list, then the team tail is inserted into the inserted at the end of the linked list. There is no problem (the tail pointer can directly point to the next), which is easy to implement, if the team head It at the head of the linked list, that is, the head node that we often mentioned earlier deletes the node .

So what we finally adopted is the singly linked list with the lead node and tail pointer of Scheme 2!

The main operations are:

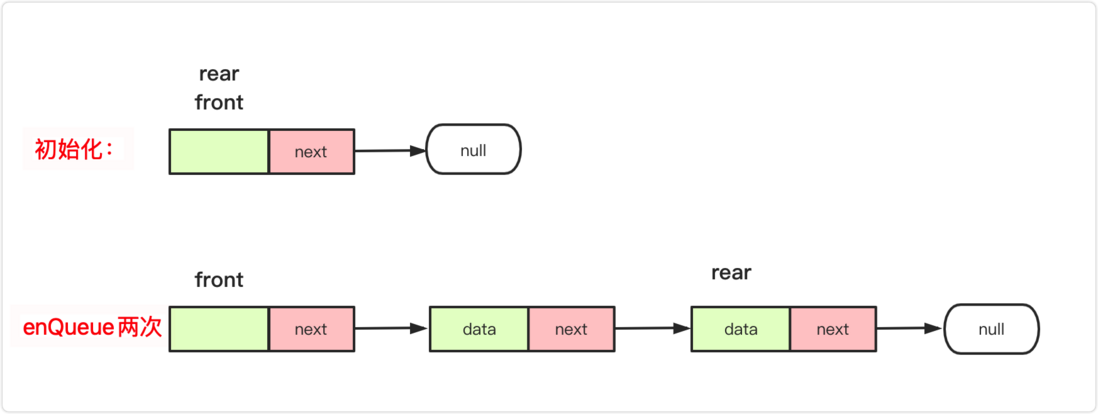
initialize : set up a head node, and both front and rear point to it first.

the team : rear.next=va;rear=va ; (va is the inserted node)

out of the team : The team is not empty, front.next=front.next.next; classic lead node is deleted, but if only one node is deleted, you need to add a rear=front, otherwise the rear will lose connection.

is empty : return rear == front; or custom maintenance len judgment return len==0

size : the number of nodes front traversed to rear, or the custom maintenance len returns directly (not implemented here).

Implementation code:

public class MyCircularQueue{
     class node {
        int data;// 节点的结果
        node next;// 下一个连接的节点
        public node() {}
        public node(int data) {
            this.data = data;
        }
    }
    node front;//相当于head 带头节点的
    node rear;//相当于tail/end
    int maxsize;//最大长度
    int len=0;
    public MyCircularQueue(int k) {
        front=new node(0);
        rear=front;
        maxsize=k;
        len=0;
    }
    public boolean enQueue(int value)  {
        if (isFull())
            return  false;
        else {
            node va=new node(value);
            rear.next=va;
            rear=va;
            len++;
        }
        return  true;
    }
    public boolean deQueue() {
        if (isEmpty())
            return false;
        else {
            front.next=front.next.next;
            len--;
            //注意 如果被删完 需要将rear指向front
            if(len==0)
                rear=front;
        }
        return  true;
    }

    public int Front() {
        if(isEmpty())
            return -1;
        return front.next.data;
    }

    public int Rear() {
        if(isEmpty())
            return -1;
        return rear.data;
    }

    public boolean isEmpty() {
        return  len==0;
        //return rear == front;
    }

    public boolean isFull() {
        return len==maxsize;
    }    
}

Two-way queue (additional meal)

Design and implement a deque. In fact, the ArrayDeque you often use is a classic two-way queue, which is based on an array and is very efficient. The two-way queue template we implemented here is based on the 641 design cyclic deque .
Your implementation needs to support the following operations:

• MyCircularDeque(k): Constructor, the size of the deque is k.
• insertFront(): Add an element to the head of the deque. If the operation is successful, return true.
• insertLast(): Add an element to the tail of the deque. If the operation is successful, return true.
• deleteFront(): Delete an element from the head of the deque. If the operation is successful, return true.
• deleteLast(): Delete an element from the tail of the deque. If the operation is successful, return true.
• getFront(): Obtain an element from the head of the deque. If the deque is empty, return -1.
• getRear(): Get the last element of the deque. If the deque is empty, return -1.
• isEmpty(): Check whether the deque is empty.
• isFull(): Check whether the deque is full.

In fact, with the above foundation, it is very easy to implement a double-ended queue. There are many operations that are consistent with single-ended circular queues. There is only one more operation of insert and delete . The two operations are simple. Analysis of:

team head is inserted into : The front subscript position of the teammate itself has a value, so the front should be backed one bit and then assigned, but it is necessary to consider whether it is full or the array is out of bounds.

end of the team: only need to subtract 1 from the rear position, and also consider whether it is empty or out of bounds.

Specific implementation code:

public class MyCircularDeque {
    private int data[];// 数组容器
    private int front;// 头
    private int rear;// 尾
    private int maxsize;// 最大长度
    /*初始化 最大大小为k */
    public MyCircularDeque(int k) {
        data = new int[k+1];
        front = 0;
        rear = 0;
        maxsize = k+1;
    }

    /** 头部插入 */
    public boolean insertFront(int value) {
        if(isFull())
            return false;
        else {
            front=(front+maxsize-1)%maxsize;
            data[front]=value;
        }
        return  true;
    }

    /** 尾部插入 */
    public boolean insertLast(int value) {
        if(isFull())
            return  false;
        else{
            data[rear]=value;
            rear=(rear+1)%maxsize;
        }
        return  true;
    }

    /** 正常头部删除 */
    public boolean deleteFront() {
        if (isEmpty())
            return false;
        else {
            front=(front+1)%maxsize;
        }
        return  true;
    }

    /** 尾部删除 */
    public boolean deleteLast() {
        if(isEmpty())
            return false;
        else {
            rear=(rear+maxsize-1)%maxsize;
        }
        return true;
    }

    /** Get the front item  */
    public int getFront() {
        if(isEmpty())
            return -1;
        return data[front];
    }

    /** Get the last item from the deque. */
    public int getRear() {
        if(isEmpty())
            return -1;
        return  data[(rear-1+maxsize)%maxsize];
    }

    /** Checks whether the circular deque is empty or not. */
    public boolean isEmpty() {
        return front==rear;
    }

    /** Checks whether the circular deque is full or not. */
    public boolean isFull() {
        return (rear+1)%maxsize==front;
    }
}

Summarize

For the queue, the data structure is more complicated than the stack, but it is not very difficult. You can understand the first-in first-out and use an array or a linked list to implement it.

For arrays, the position pointed to by tail at the end of the queue is empty, and the front (same as head) of the linked list is empty for the head pointer, so you need to pay attention to the method to achieve the same effect in different structures.

The circular queue implemented by the array can make use of the array space to a large extent, and the two-way queue is an efficient data structure that can be used as both a queue and a stack, and it is still necessary to master it.

Finally, the author's level is limited, if there are flaws and shortcomings , please also point out . In addition, if you feel good, you can like it, follow personal public number : bigsai more often to share with you, follow the reply bigsai get a copy of carefully prepared learning materials!