Understand the dictionary tree in one article

What is a dictionary tree

Dictionary tree is a space for time , also known as Trie tree, prefix tree, is a tree structure (dictionary tree is a data structure), typically used to count, sort, and save a large number of characters string. So it is often used by search engine systems for text word frequency statistics. Its advantages are: use the common prefix of the string to reduce the query time, minimize the unnecessary string comparison, and the query efficiency is higher than the hash tree.

In most cases, it may be difficult for you to be intuitive or have contact experience. You may have no idea about the prefix. You may encounter the prefix problem when you are doing the problem. It is also a violent match. Confused, but if the string is relatively long and the same prefix is many, then using the dictionary tree can greatly reduce the memory usage and efficiency. An application scenario of a dictionary tree: There will be some god-related search content below the input words in the search box. Sometimes you are very miraculous how to do it. This is actually an idea of the dictionary tree.

For the dictionary tree, there are three important properties:

1: The root node does not contain characters, except for the root node, each node contains only one character. The root node contains no characters. The purpose of this is to be able to include all strings.

2: From the root node to a certain node, passing the string is the string corresponding to the node.

3: The sub-node characters of each node are different, that is, the corresponding words and characters are unique.

Design and implement dictionary tree

What is a dictionary tree has been introduced above, so let's design a dictionary tree!

For the dictionary tree, there may be some detailed differences in the design of different scenarios or requirements, but on the whole, the general dictionary tree includes insertion, query (specified string), and query (prefix).

Let's analyze the simple situation first, that is, there are all 26 lowercase letters in the string, and it happens to be to implement Trie tree as a template for implementation.

Implement the Trie class:

• Trie() initializes the prefix tree object.
• void insert(String word) Insert the string word into the prefix tree.
• boolean search(String word) If the string word is in the prefix tree, return true (that is, it has been inserted before the search); otherwise, it returns false.
• boolean startsWith(String prefix) If one of the prefixes of the previously inserted string word is prefix, return true; otherwise, return false.

How to design this dictionary tree?

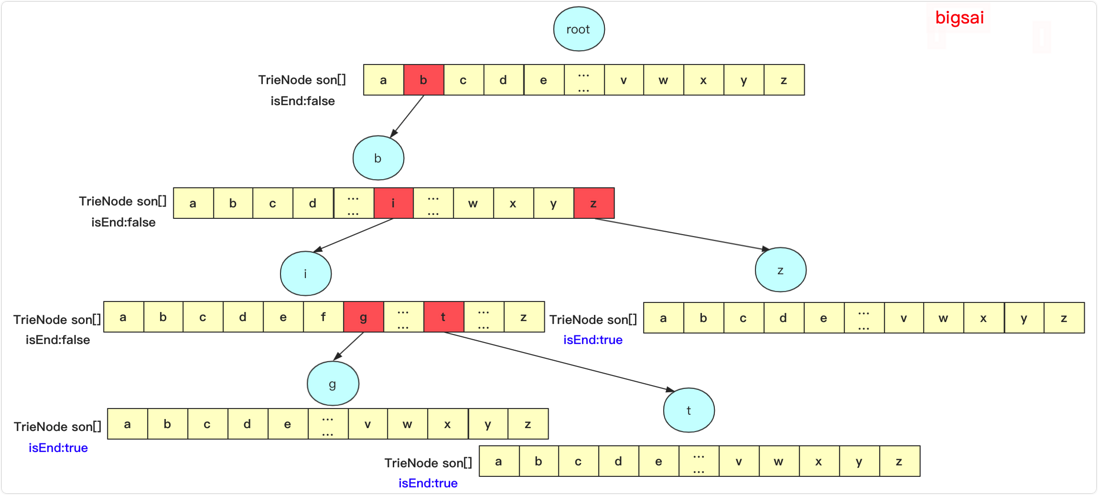
For a dictionary tree Trie class, there must be a root node root, and this node type TrieNode also has many design methods. Here we put a 26-size TrieNode type array for simplicity, corresponding to'a'-'z 'Character, at the same time a boolean type variable isEnd is used to indicate whether it is the end of the string (if it is true, it means).

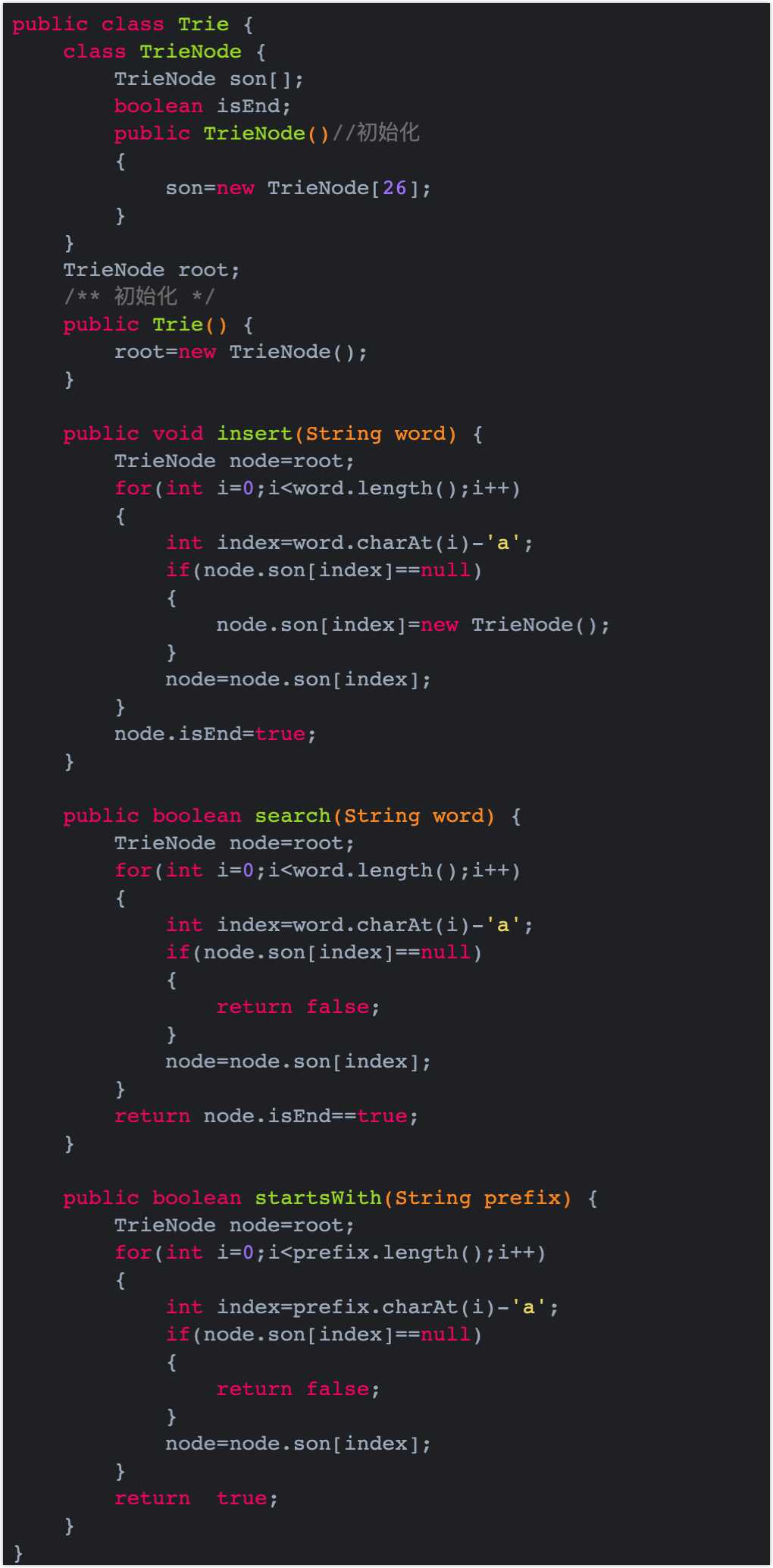
class TrieNode {
    TrieNode son[];
    boolean isEnd;//结束标志
    public TrieNode()//初始化
    {
        son=new TrieNode[26];
    }
}

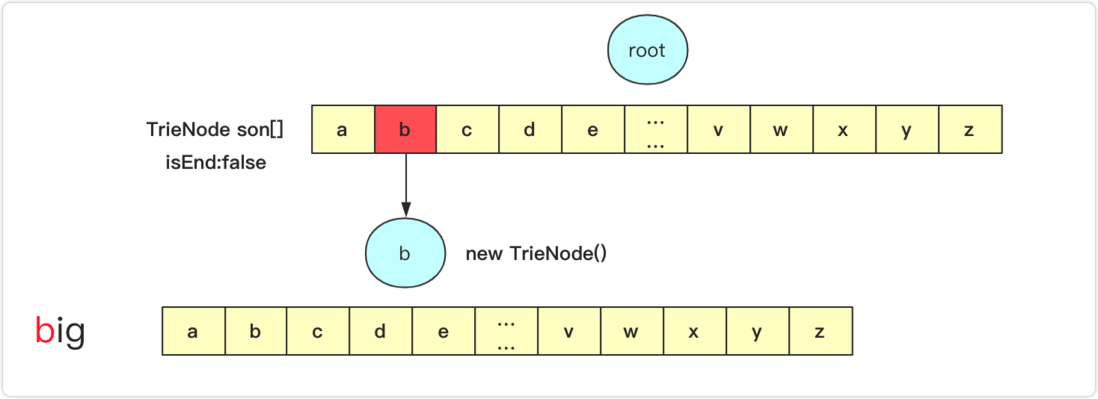
If you use an array, if there are more characters, it may consume some memory space, but 26 consecutive characters are fine here. If you add big , bit , bz to a dictionary tree, then it actually looks like this:

Then analyze the specific operations:

insert operation : traverse the string, and at the same time start traversing from the root node of the dictionary tree, find the position corresponding to each character, first determine whether it is empty, if it is empty, you need to create a new Trie. Such as inserting big enumerate the first time to create a b TrieNode, the back is the same reason. However, it is important to set isEnd to true at the stopped TrieNode to indicate that this node is the end node of the string.

The key code corresponding to this part is:

TrieNode root;
/** 初始化 */
public Trie() {
    root=new TrieNode();
}

/** Inserts a word into the trie. */
public void insert(String word) {
    TrieNode node=root;//临时节点用来枚举
    for(int i=0;i<word.length();i++)//枚举字符串
    {
        int index=word.charAt(i)-'a';//找到26个对应位置
        if(node.son[index]==null)//如果为空需要创建
        {
            node.son[index]=new TrieNode();
        }
        node=node.son[index];
    }
    node.isEnd=true;//最后一个节点
}

query operation : The query is established when the dictionary tree has been built. This process is similar to the query but does not need to create a TrieNode. If the enumeration process finds that the TrieNode is not initialized (ie, it is empty), it returns false If it goes well to the end, check whether the isEnd of the node is true (whether the string with the end of the changed character has been inserted), if it is true, return true.

It might be better to understand with an example here. Insert the big string. If you search for ba , it will be a corresponding to the second 061654ea2f32b7 is null. If the lookup bi also returns a failure, because the previously inserted big only g corresponding to TrieNode isEnd = true identification character, but i character following isEnd is false, i.e., absence bi string.

The core code corresponding to this part is:

public boolean search(String word) {
    TrieNode node=root;
    for(int i=0;i<word.length();i++)
    {
        int index=word.charAt(i)-'a';
        if(node.son[index]==null)//为null直接返回false
        {
            return false;
        }
        node=node.son[index];
    }
    return node.isEnd==true;
}

prefix search : It is similar to the query but a little bit different. If the search fails, it returns false, but if it can proceed to the last step, it returns true. In the above example, inserting big find bi also returns true, because there is a string prefixed with it.

The corresponding core code is:

public boolean startsWith(String prefix) {
    TrieNode node=root;
    for(int i=0;i<prefix.length();i++)
    {
        int index=prefix.charAt(i)-'a';
        if(node.son[index]==null)
        {
            return false;
        }
        node=node.son[index];
    }
  //能执行到最后即返回true
    return  true;
}

The above code together is a complete dictionary tree, the most basic version. The full version is:

Dictionary tree small thinking

The basic class of dictionary tree is easy, but some extensions are likely to appear.

For the above 26 characters, we can easily find the corresponding index in ASCII. If the characters are more likely and the space that may be wasted by using the array is larger, then we can also use HashMap or List to store the elements. If you use List, then You need to enumerate sequentially, and you can query directly with HashMap. Here is a dictionary tree implemented using HashMap().

Use HashMap instead of array (but using hash does not have its own sorting function). In fact, the logic is the same. You only need to use HashMap to determine whether there is a corresponding key when judging. The type of HashMap is:

Map<Character,TrieNode> sonMap;

The complete code of the dictionary tree implemented using HashMap is:

import java.util.HashMap;
import java.util.Map;

public  class Trie{
    class TrieNode{
        Map<Character,TrieNode> sonMap;
        boolean idEnd;
        public TrieNode()
        {
            sonMap=new HashMap<>();
        }
    }
    TrieNode root;
    public Trie()
    {
        root=new TrieNode();
    }
   
    public void insert(String word) {
        TrieNode node=root;
        for(int i=0;i<word.length();i++)
        {
            char ch=word.charAt(i);
            if(!node.sonMap.containsKey(ch))//不存在插入
            {
                node.sonMap.put(ch,new TrieNode());
            }
            node=node.sonMap.get(ch);
        }
        node.idEnd=true;
    }
    
    public boolean search(String word) {
        TrieNode node=root;
        for(int i=0;i<word.length();i++)
        {
            char ch=word.charAt(i);
            if(!node.sonMap.containsKey(ch))
            {
                return false;
            }
            node=node.sonMap.get(ch);
        }
        return node.idEnd==true;//必须标记为true证明有该字符串
    }


    public boolean startsWith(String prefix) {
        TrieNode node=root;
        for(int i=0;i<prefix.length();i++)
        {
            char ch=prefix.charAt(i);
            if(!node.sonMap.containsKey(ch))
            {
                return false;
            }
            node=node.sonMap.get(ch);
        }
        return true;//执行到最后一步即可
    }
}

As mentioned earlier, the dictionary tree is used for the statistics, sorting, and storage of a large number of characters. In fact, sorting is the sorting method that can be done by using an array. Because the ASCII of the characters is in order, it can be read according to this rule when reading. This idea is It's a bit similar to radix sorting.

For statistics, you may face quantitative statistics, which may be the number of occurrences or the number of prefix words. It may be a waste of time if you enumerate each time, but you can add a variable to TrieNode, and you can count the number of times each time you insert it. If the string is repeated, it can be added directly. If the string needs to be de-duplicated, it can be confirmed that the insertion is successful and then the total number of prefix words on the path will be incremented. In this case, specific issues need to be analyzed in detail.

In addition, there is a dictionary tree used in ACM to solve the problem of seeking or the most value. We call it: 161654ea2f363b 01 dictionary tree , you can also understand it if you are interested (may be introduced later).

Summarize

Through this article, you must have a better understanding of the dictionary tree. The purpose of this article is to allow readers to recognize and learn the basic dictionary tree, and have a preliminary understanding of other deformation optimizations.

The dictionary tree can minimize unnecessary string comparisons and is used for word frequency statistics and a large number of string sorting. With its own sorting function, the sorting sequence can be obtained by traversing the sequence in the middle order. But if there are many characters with the same prefix and few prefixes, then the dictionary tree has no efficiency advantage (because it needs to visit the nodes one by one).

There are many real applications of dictionary trees, such as string retrieval, text prediction, auto-completion, see also, spell checking, word frequency statistics, sorting, string longest common prefix, prefix matching for string search, as other data structures and algorithms The auxiliary structure, etc., will not be introduced here.

It’s not easy to be original, please like, follow, and collect for three consecutive support. WeChat search [ ], follow me, and get dry content as soon as possible!