Understand dynamic programming in one article

Preface

Hello everyone, I’m bigsai. I haven’t seen it for a long time and I really miss it (I miss it every day)!

A long time ago, a small partner was tortured by dynamic programming. Indeed, many problems in dynamic programming are really too difficult to see, and even some problems take a long time to understand the solution.

Although the scope of dynamic programming is indeed very wide and difficult, judging from the frequency of appearance of the entire dynamic programming, these basic dynamic programming are easy to understand, the pressure to learn is not great, and the frequency of occurrence is very high.

These common dynamic programming are: the maximum sum of consecutive subarrays, the maximum product of subarrays, the longest incremental subsequence (LIS), the longest common subsequence (LCS), the longest common substring, the longest common substring , Different subsequences.

First public number bigsai , declined to reprint without contact

What is dynamic programming

First of all, many people ask, what is dynamic programming? Dynamic Programming (Dynamic Programming, DP) is a branch of operations research, which is the process of solving the optimization process of decision-making. A popular point of dynamic programming is to solve the numerical value stepwise from bottom to top (from front to back).

So what is the difference and connection between dynamic programming and recursion?

Generally speaking, dynamic programming is from front to back, and recursion is from back to front. The two strategies are different, and the efficiency of dynamic programming is generally higher than that of recursion.

However, the initial state and the connection between the upper and lower data must be considered. Many times the problems that can be solved by dynamic programming can also be solved by recursion, but in many cases, the efficiency is not high and memory search may be used.

do not understand?

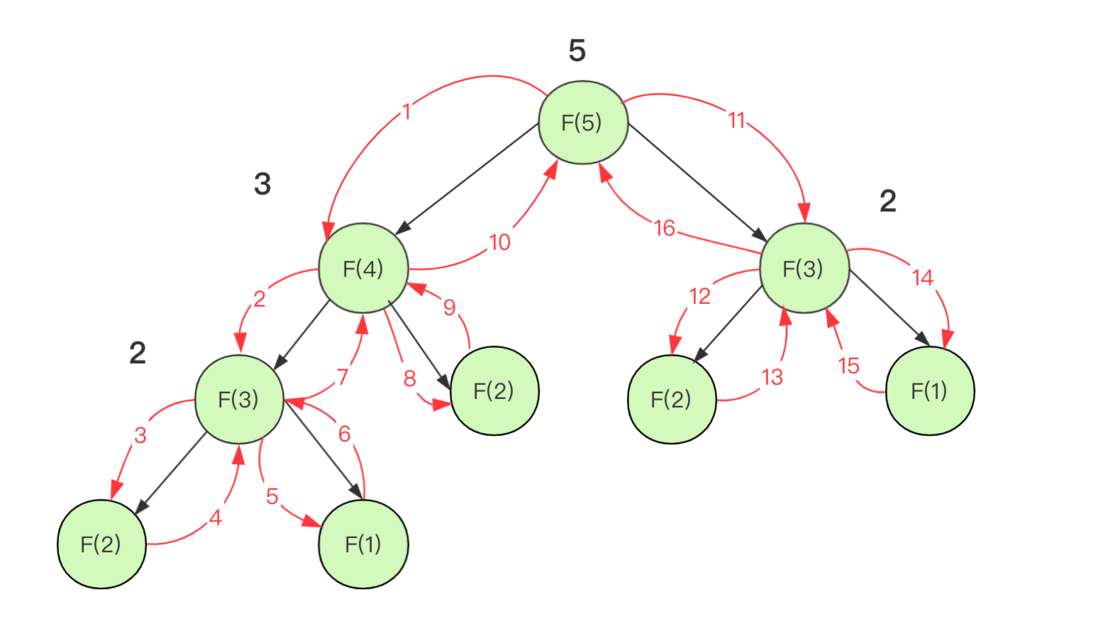
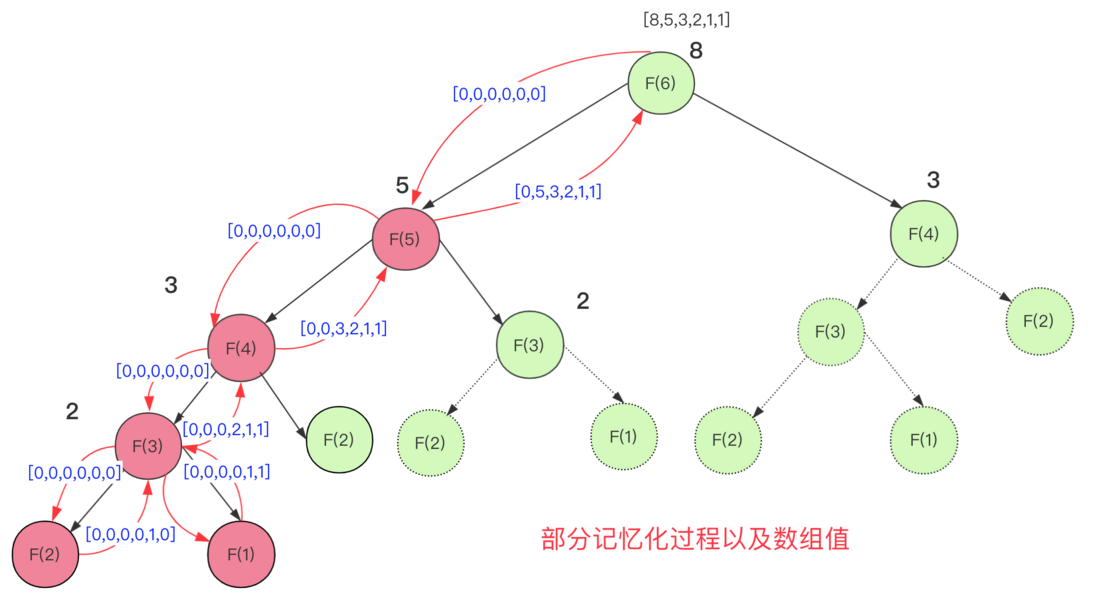
Take solving the Fibonacci number sequence as an example. If recursion is used directly without optimization, then the complexity will be too much and a lot of repeated calculations will be carried out.

But using memoization, you can understand it as a layer of caching, and save the calculated value and use it directly when you encounter it next time.

The Fibonacci code for achieving memory search is:

static long F(int n,long record[])
{
  if(n==1||n==2) {return 1;}
  if(record[n]>0)
    return record[n];
  else
    record[n]=F(n-1,record)+F(n-2,record);
  return record[n];
}
public static void main(String[] args) {
  int n=6;
  long[] record = new long[n+1];
  System.out.println(F(n,record));
}

With dynamic programming, you can process logically from front to back, starting from the third, each dp is the sum of the first two dp.

 public int fib(int n) {
        int dp[]=new int[n+1];
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<n+1;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

Of course, dynamic programming can also have a lot of space optimizations, some of which are only used once, you can use some variables to replace them. Some two-dimensional arrays are very large and can be alternately replaced with one-dimensional arrays. Of course, the dynamic planning topic is very large. There are many such as tree dp, state pressure dp, backpack problems, etc. that often appear in the competition, and the ability is limited. Here will be some dynamic planning with high frequency of written tests!

Maximum sum of consecutive subarrays

Given an integer array nums, find a continuous sub-array with the largest sum (the sub-array contains at least one element), and return the largest sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The sum of consecutive sub-arrays [4,-1,2,1] is the largest, which is 6.

The dp method is the O(n) method. If dp[i] represents the largest sequence ending with the i-th and , the state equation of this dp is:

dp[0]=a[0]
dp[i]=max(dp[i-1]+a[i],a[i])

It is not difficult to explain, if the previous maximum subsequence sum is greater than 0, then this element is connected, otherwise this element will stand on its own.

The implementation code is:

public int maxSubArray(int[] nums) {
    int dp[]=new int[nums.length];
    int max=nums[0];
    dp[0]=nums[0];
    for(int i=1;i<nums.length;i++)
    {
      dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
      if(dp[i]>max)
        max=dp[i];
    }
    return max;
}

ps: Some friends ask, what about the maximum sum of an array that can be discontinuous? Think about it carefully and enumerate the positive income pockets. That question is meaningless.

Maximum product of consecutive subarrays

Given an integer array nums, please find the continuous sub-array with the largest product in the array (the sub-array contains at least one number), and return the product corresponding to the sub-array.

Example:

Input: [2,3,-2,4]
Output: 6
Explanation: The sub-array [2,3] has a maximum product of 6.

The maximum product of consecutive sub-arrays is also a classic dynamic programming problem, but it is a bit different from ordinary dynamic programming.

If the data are all non-negative numbers , for the maximum product of a continuous array, the processing is similar to the previous continuous sub-array maximum and the processing is similar, either with the previous multiplication or independent.

dp[0]=nums[0]
dp[i]=max(dp[i-1]*a[i],a[i])

But the data inside will appear negative number , multiplied by a negative number, it may change from the largest to the smallest, and there is a negative negative to positive and it may become the largest.

What should we consider at this time?

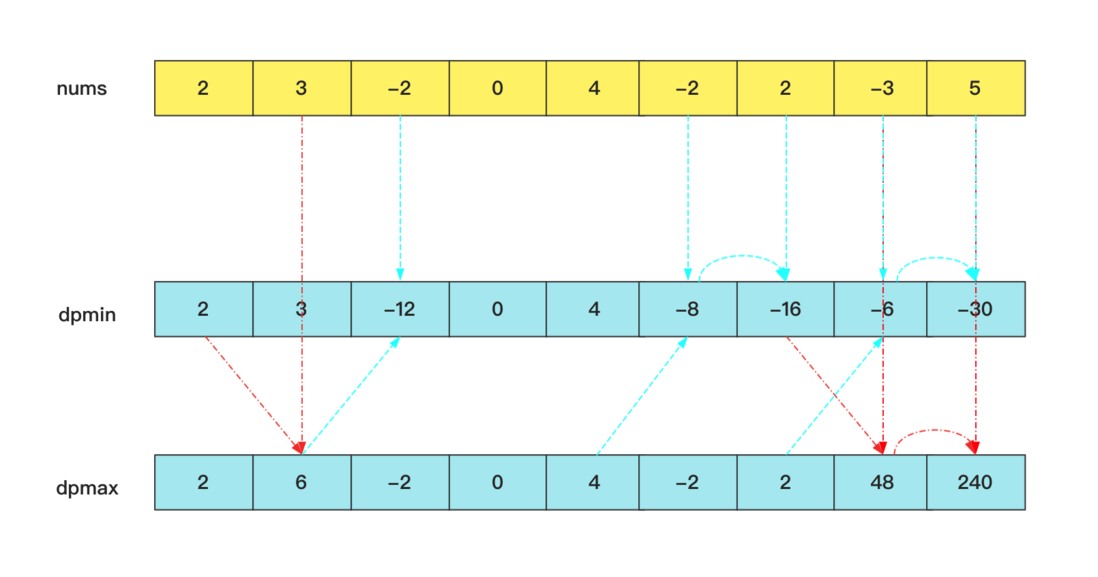
Easy, we open two dp, one dpmax[] records the maximum value of the product, and one dpmin[] records the minimum value of the product. Then updated every time dpmax and dpmin regardless of the current value is positive or negative. In this way by these two arrays can record the product absolute value of the maximum .

Dynamic equations are also easy

dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])

See appreciated that a process can be appreciated, dpmin is to play the role of an intermediate excessive, some of the possible record negative value prevent backup. The result is still the value in dpmax.

Longest increasing subsequence

The longest increasing subsequence, also called LIS, is one of the dynamic programming algorithms that appear very high frequency. Here for stress buckle 300

Give you an integer array nums and find the length of the longest strictly increasing subsequence.

A subsequence is a sequence derived from an array, deleting (or not deleting) elements in the array without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Input: nums = [0,1,0,3,2,3]
Output: 4
Explanation: The longest increasing subsequence is [0,1,2,3], so the length is 4.

For the longest increasing subsequence, if you don't consider the dynamic programming method, it is actually more troublesome to use violent enumeration, because you don't know whether to increase if you encounter a larger element than the previous one.

For example, 1 10 3 11 4 5, this sequence cannot choose 1 10 11 and 1 3 4 5 is the largest, so the time complexity of violently enumerating all situations is still very high.

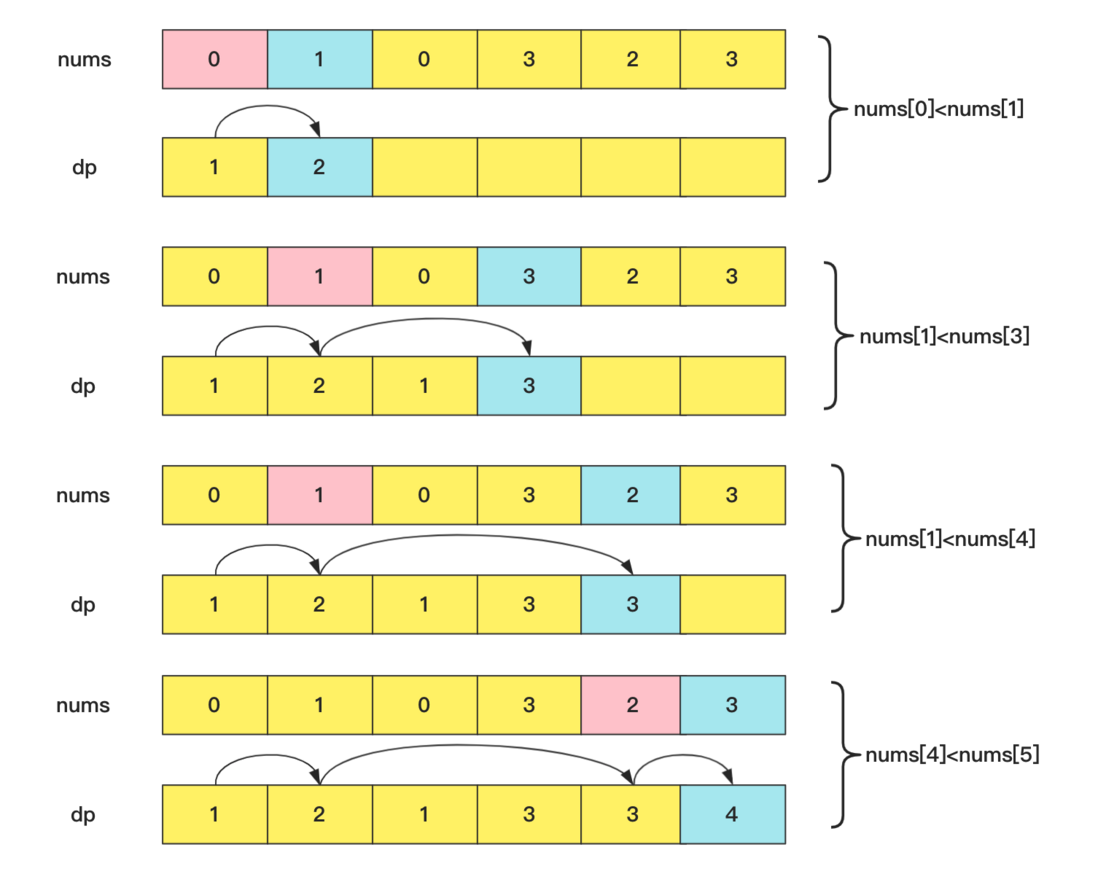
If we take the dynamic programming method and create the dp[] array, dp[i] represents nums[i] ending in 0618a157be1ccf, and the solution of dp[i] is to enumerate the elements before the i number and the longest subsequence at the end. Sequence, find an element value less than nums[i] and the longest increasing sequence, this time complexity is O(n2).

The state transition equation is:

dp[i]=max(dp[j])+1, 其中0≤j<i且num[j]<num[i]

The specific process is:

The implementation code is:

class Solution {
    public int lengthOfLIS(int[] nums) {
        int dp[]=new int[nums.length];
        int maxLen=1;
        dp[0]=1;
        for(int i=1;i<nums.length;i++){
            int max=0;//统计前面 末尾数字比自己小 最长递增子串
            for(int j=0;j<i;j++){//枚举
                //结尾数字小于当前数字 并且长度大于记录的最长
                if(nums[j]<nums[i]&&dp[j]>max){
                    max=dp[j];
                }
            }
            dp[i]=max+1;//前面最长 加上自己
            if(maxLen<dp[i])
                maxLen=dp[i];
        }
        return maxLen;
    }
}

However, there is an optimization for this problem, which can be optimized to O(nlogn) time complexity.

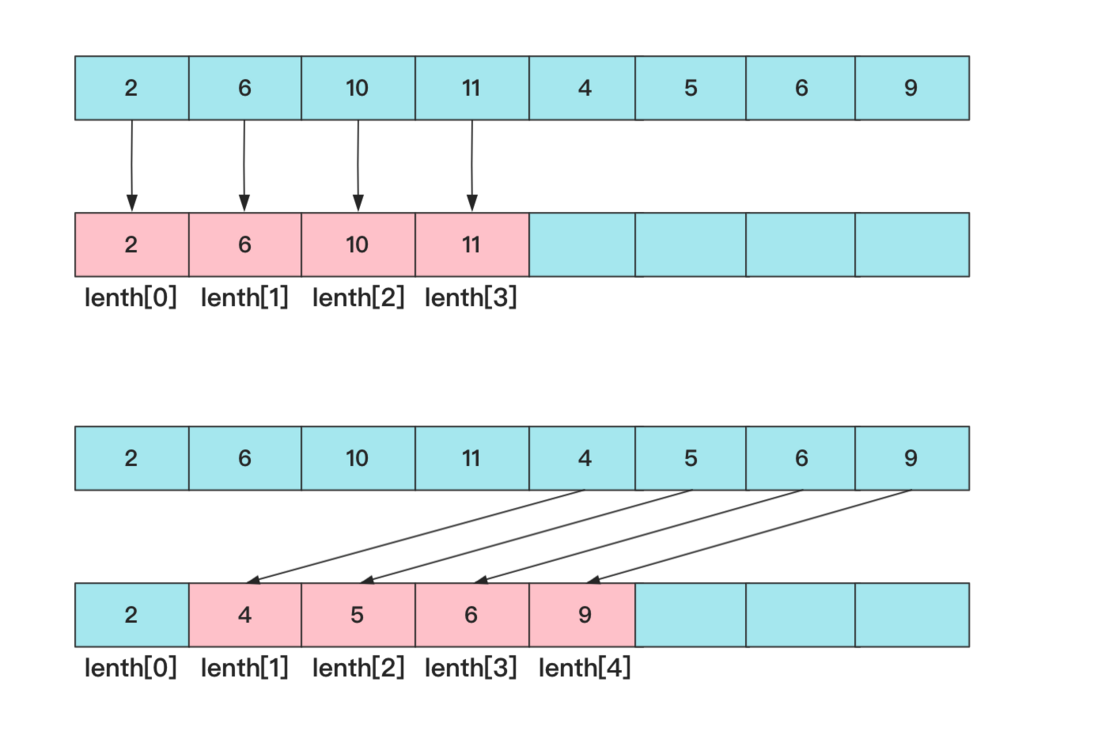
We use dp to record the nums[i] ending in 0618a157be1db2. Looking at the overall situation, we hope that the value at the end can be as small as possible when the length is the same!

For example, 2,3,9,5...... The longest length in the front is 3. We are willing to abandon 2,3,9 and use 2,3,5 all. That it is, for a value, we hope that this value can be updated at the end of the value to it as the end of the longest sequence of .

If this value cannot update the longest sequence, then try to update the second-longest end value to prevent it from being used. For example, 2,3,9,5,4,5 this sequence 2,3,5 update 2,3,9; then 2,3,4 update 2,3,5 as the longest 2,3,4,5 do bedding.

The core of this idea is to maintain an lenth[] , length[i] represents the minimum value of the end of the subsequence of length i, because each time we increase the means that this value is larger than the previous one (full comparison) , So this array is also an increment of dichotomy optimization can be used when updating the maximum length sequence tail value at the locked position.

The implementation code is:

class Solution {
    public int lengthOfLIS(int[] nums) {
        int length[]=new int[nums.length];
        int len=1;
        length[0]=nums[0];
        for(int i=1;i<nums.length;i++){
            int left=0,right=len;
            while (left<right){
                int mid=left+(right-left)/2;
                if(length[mid]<nums[i]){
                    left=mid+1;
                }else {
                    right=mid;
                }
            }
            length[left]=nums[i];
            if(right==len)
                len++;        
        }
        return len;
    }
}

Longest common subsequence

The longest common subsequence also becomes LCS. The frequency of occurrence is very high!

Given two strings text1 and text2, return the length of the longest common subsequence of these two strings. If there is no common subsequence, 0 is returned.

A subsequence of a character string refers to a new character string: it is a new character formed by deleting certain characters (or not deleting any characters) of the original character string without changing the relative order of string.

For example, "ace" is a subsequence of "abcde", but "aec" is not a subsequence of "abcde".
The common subsequence of two strings is the subsequence shared by the two strings.

Take bcdde and aceede for example, the common substring is cde. If you use brute force, the complexity will be too high and it will directly time out, you need to use dynamic programming. Two strings match, we set up a two-dimensional array dp[][] dp[i][j] represents the i-th end of the text1 string, and the length of the longest common substring .

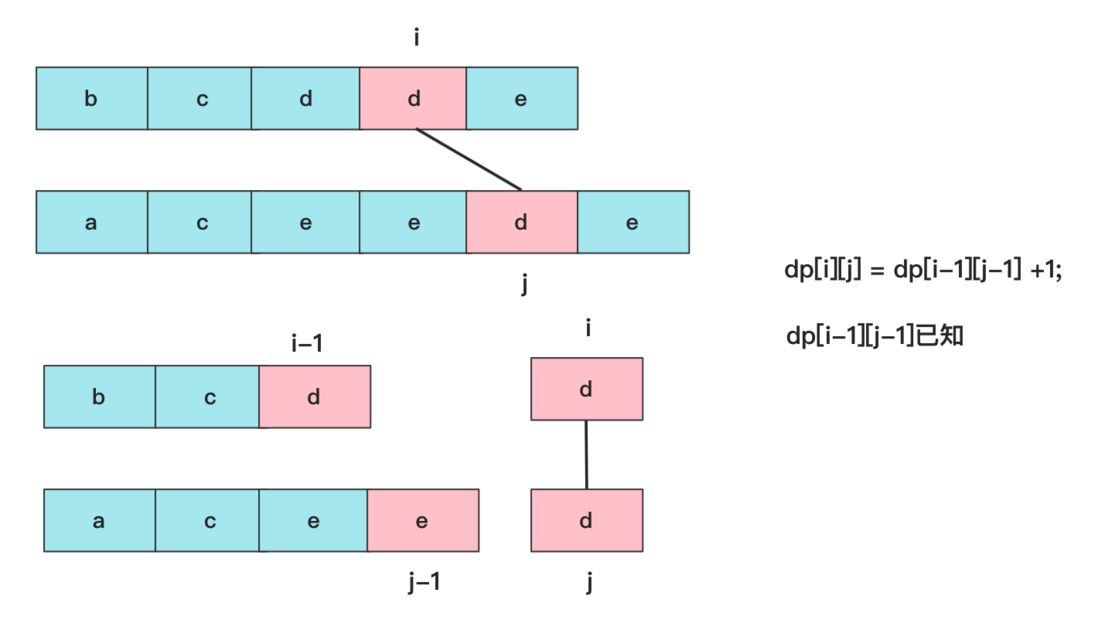
The core here is to understand the state transition, analyze dp[i][j] , when it reaches i, j:

If text1[i]==text2[j] , because both elements in the rearmost position, it will be able to match the success of , in other words, a neighbor dp value of this location can not be greater than he (most equal). So this time is dp[i][j] = dp[i-1][j-1] + 1 ;

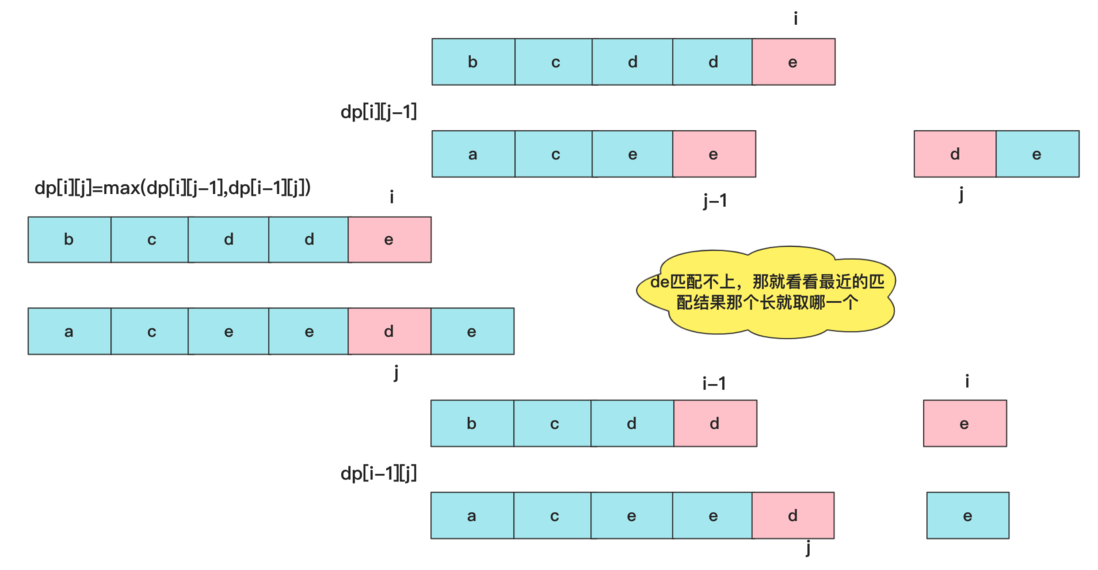
If text1[i]!=text2[j] , there are two possibilities, we know that the neighbors have dp[i-1][j] , dp[i][j-1] , many people will think dp[i-1][j-1] this must be less than the previous two, because that is in front of two sub-ranges Well! So at this time, it is equivalent to the end of the match is not matched, you have to look at the maximum value that the neighbor can match, at this time dp[i][j] = max(dp[i][j-1],dp[i-1][j]) .

So the entire state transition equation is:

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]时
dp[i][j] = max(dp[i][j-1],dp[i-1][j])  //text1[i]!=text2[j]时

The implementation code is:

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        char ch1[]=text1.toCharArray();
        char ch2[]=text2.toCharArray();
        int dp[][]=new int[ch1.length+1][ch2.length+1];
        for(int i=0;i<ch1.length;i++)
        {
            for(int j=0;j<ch2.length;j++)
            {
                if(ch1[i]==ch2[j])
                {
                    dp[i+1][j+1]=dp[i][j]+1;
                }
                else
                    dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j]);

            }
        }
        return dp[ch1.length][ch2.length];
    }
}

Longest common substring

Given two strings str1 and str2, output the longest common substring of the two strings.

For example, the longest common substring of abceef and a2b2cee3f is cee. The common substring is the longest continuous identical part of the two strings.

How to analyze it? Similar to the analysis method of the longest common subsequence above, dynamic programming matching is required, and the logical processing is simpler. As long as the current i and j do not match, the dp value is 0, and if it can be matched, it becomes dp[i-1][j-1] + 1

The core state transition equation is:

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]时
dp[i][j] = 0  //text1[i]!=text2[j]时

The code here is very similar to the above, so I won't write it, but there is a problem that will cause you to output the longest string. You have to remember to use some variables to store the value.

Different subsequences

Different sequences will appear, and some difficulty, earlier in this different subsequence problem analysis tell everyone can see.

Given a string s and a string t, count the number of occurrences of t in the subsequence of s.

A subsequence of a string refers to a new string formed by deleting some (or not deleting) characters without disturbing the relative positions of the remaining characters. (For example, "ACE" is a subsequence of "ABCDE", but "AEC" is not)

Example:

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

analysis:
This question is actually the deformation and expansion of several pats above. The basic idea is actually the same. The question above is about several pats, which are fixed and very short. But the length of the t string is not fixed, so the array must be used for processing instead of if else directly.

The idea of this question must also be dynamic programming dp. dp[j] means the number of [0,j-1] long characters in the t string that can be matched in s (of course, this value changes dynamically from front to back), the size of the array is dp[t.length+1] . Each element in the traversal s string must be compared with all the elements in the t string to see if they are equal. If the string enumerated by the s string is equal to the jth string in the t string. Then dp[j+1]+=dp[j] . You may ask why it is dp[j+1] , because the first element is matched to the number of +1, and in order to avoid such a judgment, we will dp[0]=1 , so that each element of the t string can operate normally.

But one thing to note is that when traversing the i-th letter in the s string, traverses the t string from left to right and must be from right to left. Because when traversing the i-th character of the s string when enumerating the dp array, it is required that the data is relatively static at the moment (that is, the same level cannot have an impact), and encountering the same character from left to right will affect the subsequent value . The difference can refer to the example below:

The implemented code is:

class Solution {
    public int numDistinct(String s, String t) {
      char s1[]=s.toCharArray();
      char t1[]=t.toCharArray();
      int dp[]=new int[t1.length+1];
      dp[0]=1;//用来叠加

      for(int i=0;i<s1.length;i++)
      {
        for(int j=t1.length-1;j>=0;j--)
        {
          if(t1[j]==s1[i])
          {
            dp[j+1]+=dp[j];
          }
        }
      }
      return dp[t1.length];
    }
}

Concluding remarks

At this point, the simple dynamic programming can be regarded as finished sharing.

Most simple dynamic programming still has routines. If you see some array problems or string problems, it is very likely that dynamic programming is hidden. The routine of dynamic programming is a bit similar to recursion. The main thing is to find the state transition equation. Sometimes you can’t think too much about the problem in one step (think too much and you may get yourself in), and dynamic programming requires everyone to convert values up and down. Calculations need to understand the relationship.

It is really difficult to see complex dp problems or many sets of one-layer shells, but mastering the common dp problems and backpack problems above can solve most of the dynamic programming problems (after all, we are not in competitions or encountered simple or medium difficulty of).

Originality is not easy, ask for a triple ! Recently, I own original article into a data structure and algorithm pdf, a total of 218 pages will be updated and maintained regularly, and reply to [ 666 ] on my public account [bigsai] to receive it!