Design an LRU efficiently

Preface

Hello everyone, I’m bigsai, I haven’t seen it for a long time, I really miss it!

Recently, a small partner complained to me that he had not met LRU. He said that he knew a long time ago that someone had been asked about LRU but thought that he might not meet him, so he was not prepared for the time being.

Unfortunately, this has really passed the test! His mood at the moment can be proved with a picture:

He said that he finally staggered to write an LRU that was not very efficient, and the interviewer looked unsatisfied... and then it was really GG.

To prevent you from encountering this pit in the future, I stepped on this pit with everyone today. I used a more ordinary method for this question myself at the beginning, but although the good method is not difficult, it took a long time to think about it, although Too much time is not worth it, I finally figured it out by myself, and I will share this process with everyone (only from the perspective of the algorithm, not from the perspective of the operating system).

Understand LRU

To design an LRU, you have to know what an LRU is, right?

LRU, the full English name is Least Recently Used, translated into algorithm has not been used the longest recently, is a commonly used page replacement algorithm .

Speaking of page replacement algorithm, which is larger relationship with the OS, and we all know that memory is faster, but the memory of capacity is very limited, it is impossible for all pages loaded into memory, so we need a The strategy pre-places frequently used pages into memory.

But, no one knows which memory the process will access next time, and it is not very effective to know (we do not currently predict the future function), so some page replacement algorithms are only idealized but can not be implemented in real (yes It is the optimal replacement algorithm (Optimal), and then the common must-return algorithms are FIFO (first in first out) and LRU (the least recently used).

LRU is not difficult to understand, that is, to maintain a fixed-size container, the core is the two operations of get() and put().

Let's first look at the two operations that LRU will have:

initialize : LRUCache(int capacity), initialize the LRU cache with a positive integer as the capacity capacity.

query : get(int key), find out whether there is a value corresponding to the current key from the data structure of your own design, if so, return the corresponding value and update the key as the most recently used, if not return -1.

insert / update : PUT (int Key, int value), may be insert a key-value, it may be update a key-value, if the container already exist before this key-value then only The corresponding value needs to be updated and marked as the latest. If this value does not exist in the container, consider whether the container is full. If it is full, delete the key-value pair that has not been used for the longest time.

The process here can give you an example, for example

容量大小为2：
[ "put",  "put", "get", "put","get", "put","get","get","get"]
[ [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1],  [3], [4]]

The process is as follows:

Details that are easy to overlook are:

• There is an update operation for put(), for example, put(3,3), put(3,4) will update the operation with key 3.
• get() may not be queried, but if queried, the least-used sequence will also be updated.
• If the container is not full, then the put may be updated and inserted, but it will not be deleted; if the container is full and the put is inserted, it is necessary to consider deleting the key-value that has not been used for the longest time.

How should we deal with such a rule above?

If you only use a List-like list , you can store the key-value pairs in sequence. We think it is relatively long before List (0 subscript is before), and we think it is relatively new after List. We consider that various operations may be designed like this:

If you come to get operation:

Traverse the List one by one to see if there is a key-value pair for the key. If there is a key-value pair, return the value of the corresponding key directly, if not, then return -1.

If you come to put operation:

Traverse the List, If there is a , then decisively delete the key-value, and finally insert the key-value pair at the end.

If there is no corresponding key and the List container has reached the fullest, then decisively delete the key-value in the first position.

Using List may require two (one for key and one for value), or a list of Node nodes (key and value are attributes). Consider this time complexity:

Put operation: O(n), get operation: O(n) Both operations require the linear complexity of enumerating the list. The efficiency is a bit sloppy, and it definitely won't work. I won't write such code.

Initial Hash Optimization

From the above analysis, we can already write LRU with confidence, but now we have to consider an optimization thing.

If we introduce a hash table into the program, there will definitely be some optimizations. Using a hash table to store key-value, the operation of querying whether it exists can be optimized to O(1), but the complexity of deleting or inserting or updating the position may still be O(n), let's analyze it together:

The longest unused must be stored in an ordered sequence, either a sequential list (array) or a linked list. If it is an array-implemented ArrayList, this sequence has not been used for the longest time.

If the ArrayList deletes the longest unused (first) key-value, the new key is hit and becomes the latest used (delete first and then insert the end) operation is O(n).

In the same way, most of the operations of LinkedList are O(n), such as deleting the first element because of the data structure O(1).

You find that your optimization space is actually very, very small, but there is indeed progress, but you are stuck and don’t know how to optimize the double O(1) operation. I put out this version of the code here, and you can refer to it ( If the interview asks, I really can’t write like this)

class LRUCache {

    Map<Integer,Integer>map=new HashMap<>();
    List<Integer>list=new ArrayList<>();
    int maxSize;
    public  LRUCache(int capacity) {
        maxSize=capacity;
    }

    public int get(int key) {
        if(!map.containsKey(key))//不存在返回-1
            return -1;
        int val=map.get(key);
        put(key,val);//要更新位置 变成最新 很重要！
        return val;
    }

    public void put(int key, int value) {
        //如果key存在，直接更新即可
        if (map.containsKey(key)) {
            list.remove((Integer) key);
            list.add(key);
        } else {//如果不存在 要插入到最后，但是如果容量满了需要删除第一个(最久)
            if (!map.containsKey(key)) {
                if (list.size() == maxSize) {
                    map.remove(list.get(0));
                    list.remove(0);
                }
                list.add(key);
            }
        }
        map.put(key, value);
    }
}

Hash + double-linked list

Above we already know that we can directly find this element with a hash, but delete ! Using List is very laborious.

In more detail, because of the delete operation of the List, the delete and insert of the Map is still very efficient.

In the above situation, what we hope is to be able to quickly delete any element in the List, and the efficiency is very high, if you can only locate it with the help of hash, but it cannot be deleted! what can we do about it?

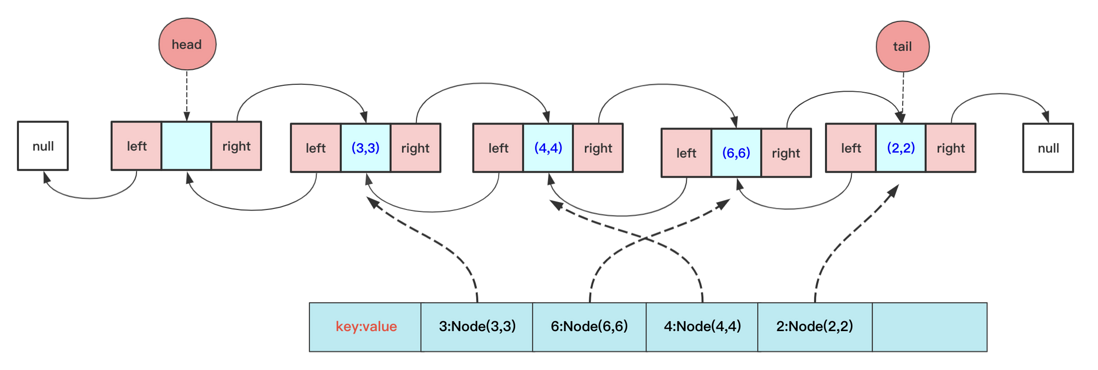
hash + double-linked list!

We store the key-val data in a Node class, and then each Node knows the left and right nodes, and directly stores them in the Map when inserting the linked list, so that the Map can directly return the node when querying, and the double-linked list knows the left and right nodes. You can directly delete the node in the double-linked list.

Of course, for efficiency, the double- watchband 161b171425cb41 implemented here has a head node (the head pointer points to an empty node to prevent abnormalities such as deletion) and a tail pointer.

For this situation, you need to be able to write linked lists and double-linked lists. The addition, deletion, and modification of double-linked lists have been clearly written. Don't worry, friends, here I have sorted them out:

Single linked list: https://mp.weixin.qq.com/s/Cq98GmXt61-2wFj4WWezSg

Double-linked list: https://mp.weixin.qq.com/s/h6s7lXt5G3JdkBZTi01G3A

That is, you can directly get the corresponding Node in the double-linked list through HashMap, and then delete it according to the relationship between the front and rear nodes, and some special cases such as null and tail pointer deletion to be considered during the period.

The specific implementation code is:

class LRUCache {
    class Node {
        int key;
        int value;
        Node pre;
        Node next;

        public Node() {
        }

        public Node( int key,int value) {
            this.key = key;
            this.value=value;
        }
    }
    class DoubleList{
        private Node head;// 头节点
        private Node tail;// 尾节点
        private int length;
        public DoubleList() {
            head = new Node(-1,-1);
            tail = head;
            length = 0;
        }
        void add(Node teamNode)// 默认尾节点插入
        {
            tail.next = teamNode;
            teamNode.pre=tail;
            tail = teamNode;
            length++;
        }
        void deleteFirst(){
            if(head.next==null)
                return;
            if(head.next==tail)//如果删除的那个刚好是tail  注意啦 tail指针前面移动
                tail=head;
            head.next=head.next.next;

            if(head.next!=null)
                head.next.pre=head;
            length--;
        }
        void deleteNode(Node team){

            team.pre.next=team.next;
            if(team.next!=null)
                team.next.pre=team.pre;
            if(team==tail)
                tail=tail.pre;
           team.pre=null;
           team.next=null;
            length--;
        }
        public String toString() {
            Node team = head.next;
            String vaString = "len:"+length+" ";
            while (team != null) {
                vaString +="key:"+team.key+" val:"+ team.value + " ";
                team = team.next;
            }
            return vaString;
        }
    }
    Map<Integer,Node> map=new HashMap<>();
    DoubleList doubleList;//存储顺序
    int maxSize;
    LinkedList<Integer>list2=new LinkedList<>();

    public   LRUCache(int capacity) {
        doubleList=new DoubleList();
        maxSize=capacity;
    }
    public  void print(){
        System.out.print("maplen:"+map.keySet().size()+" ");
        for(Integer in:map.keySet()){
            System.out.print("key:"+in+" val:"+map.get(in).value+" ");
        }
        System.out.print("              ");
        System.out.println("listLen:"+doubleList.length+" "+doubleList.toString()+" maxSize:"+maxSize);
    }

    public int get(int key) {
        int val;
        if(!map.containsKey(key))
            return  -1;
        val=map.get(key).value;
        Node team=map.get(key);
        doubleList.deleteNode(team);
        doubleList.add(team);
        return  val;
    }

    public void put(int key, int value) {
        if(map.containsKey(key)){// 已经有这个key 不考虑长短直接删除然后更新
           Node deleteNode=map.get(key);
            doubleList.deleteNode(deleteNode);
        }
        else if(doubleList.length==maxSize){//不包含并且长度小于
            Node first=doubleList.head.next;
            map.remove(first.key);
            doubleList.deleteFirst();
        }
       Node node=new Node(key,value);
        doubleList.add(node);
        map.put(key,node);

    }
}

In this way, an LRU with O(1) complexity for both get and put is written!

end

After reading the solution, I found out that LinkedHashMap in Java is almost this kind of data structure! It takes a few lines to solve it, but the average interviewer may not agree with it, and hope that everyone can write a double-linked list by hand.

class LRUCache extends LinkedHashMap<Integer, Integer>{
    private int capacity;
    
    public LRUCache(int capacity) {
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }

    public int get(int key) {
        return super.getOrDefault(key, -1);
    }

    public void put(int key, int value) {
        super.put(key, value);
    }

    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity; 
    }
}

Although the hash + double-linked list was figured out without looking at the solution of the problem, it really took a long time to think of this point. It was really rare before, and the efficient handwritten LRU can be regarded as a truly complete mastery today!

However, in addition to LRU, other page replacement algorithms are very high-frequency both in written examinations and interviews. Please sort them out by yourself if you have time.

First public number: bigsai Reprinted, please place the link between the author and the original text (this article), and share them regularly. Welcome to punch in and learn to communicate!