I was asked TopK questions in the interview, which can be answered elegantly

Preface

Hello, everyone, I’m bigsai brother. I haven’t seen each other for a long time. I really miss it 🤩!

Today I will share with you a TOPK problem, but I will not consider a particularly large distributed solution here, a common algorithm problem.

First find out, what is the topK problem?

The topK problem is to find the top k large (or small) numbers in the sequence. The topK problem and the K-th large (or small) problem-solving idea are roughly the same.

TopK question is a very classic question. It written test and interview (Never tell lies). Next, from Xiao Xiaobai's starting point, I think that topK is a problem of seeking the top K, let's get to know TopK together!

At present, the solution to TopK and the Kth largest problem is similar. Here we use to buckle the kth largest element of the 215 array, as a demonstration of the solution. Before learning topk, this programmer must know the top ten rankings must know.

Sorting method

Find TopK, and sort TopK

What, you want me to find TopK? Not only TopK, how many do you want, how many will I give you, and sort it out for you, what sort of which I am most familiar with?

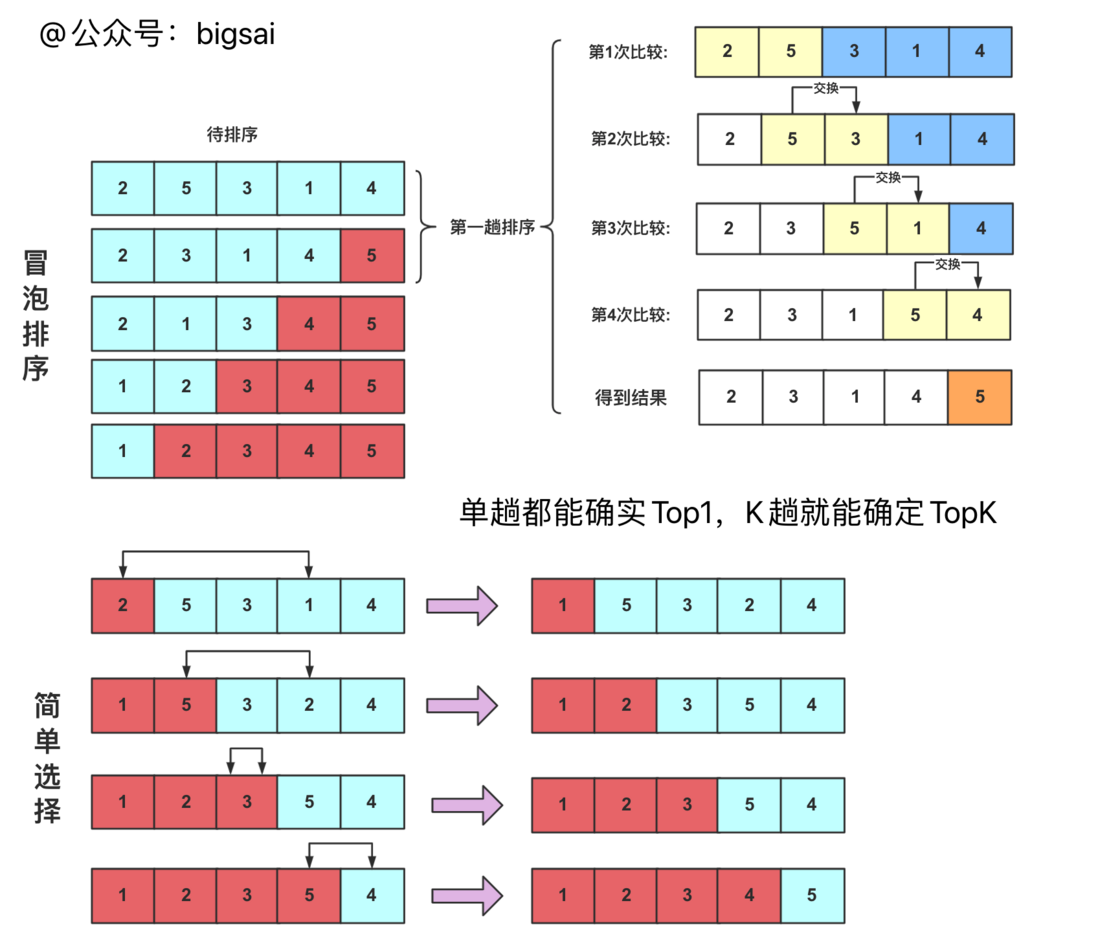
If you think of bubble sorting O(n^2), then you are careless.

If you use O(n^2)-level sorting algorithm, it is also to be optimized. Among them, bubble sorting and simple selection sorting, each pass can determine a maximum (minimum) value sequentially, so there is no need to put all the data They are all sorted out and only need to be executed K times, so the this algorithm is also O(nk) .

Here is a review of the difference between bubble sort and simple selection sort:

Bubble sorting and simple selection sorting are both multiple passes. Each pass can determine a maximum or minimum. The difference is that the bubbling is only compared with itself during the enumeration process, and exchanged if it is larger than the latter; while the simple choice is every Mark a maximum or minimum number and position at a time, and then exchange it with the last position number of this pass (determine a number in each pass and the enumeration range gradually becomes smaller).

The following diagram shows the process:

Here is the code for everyone. Simply choose the picture above to choose the smallest one each time, and choose the largest one each time you implement it.

//交换数组中两位置元素
private void swap(int[] arr, int i, int j) {
  int temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}
//冒泡排序实现
public int findKthLargest1(int[] nums, int k) {
  for(int i=nums.length-1;i>=nums.length-k;i--)//这里也只是k次
  {
    for(int j=0;j<i;j++)
    {
      if(nums[j]>nums[j+1])//和右侧邻居比较
      {
        swap(nums,j,j+1);
      }
    }
  }
  return nums[nums.length-k];
}
//简单选择实现
public int findKthLargest2(int[] nums, int k) {
  for (int i = 0; i < k; i++) {//这里只需要K次
    int max = i; // 最小位置
    for (int j = i + 1; j < nums.length; j++) {
      if (nums[j] > nums[max]) {
        max = j; // 更换最小位置
      }
    }
    if (max != i) {
      swap(nums, i, max); // 与第i个位置进行交换
    }
  }
  return nums[k-1];
}

Of course, fast sorting, merge sorting and even heap sorting are also possible. The time complexity of these sorts is O(nlogn), that is, all the data is sorted and the result is returned directly. This part will not be explained in detail, adjust the api or Handwriting can be sorted.

In the two ways of thinking, except for the case where K is extremely small, O(nk) is faster. In most cases, O(nlogn) is faster. However, from O(n^2) to O(nk), there are still gains. .

Based on heap optimization

Here you need to know the knowledge about the heap. I have written about priority queues and heap sorting before, so I won’t repeat them here. You can also take a look:

priority queue do not know, look at the heap sorting

hard core, handwriting a priority queue

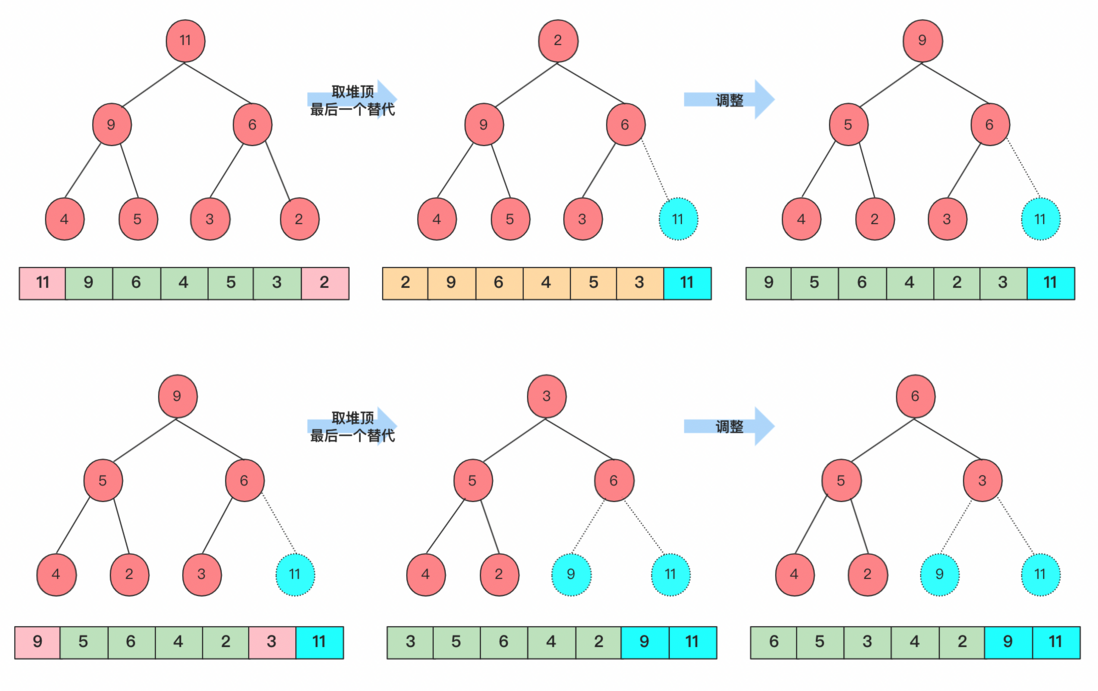
The above said that the heap sort O(nlogn) is to sort all the elements and then take the first k, but in fact, let’s analyze the process of this heap sort and several points of attention:

The data structure of the heap is divided into a large root heap and a small root heap. The small root heap means that the value of the parent node is smaller than the value of the child node, and the big root heap means that the value of the parent node is greater than the value of the child node. Here, the big root heap must be used.

The heap looks like a tree structure, but the heap is a complete binary tree. We use arrays to store very efficiently, and it is also very easy to use subscripts to directly find the parent and child nodes, so arrays are used to implement the heap. Each time the sorted node will be The number is moved to the end of the array to allow a new array to form a new heap and continue.

Heap sorting can be divided into two parts from a big point of view, the unordered array building and the top sorting each time on the basis of the heap. Among them, the time complexity of . Sorting on the basis of the heap takes the top element of the heap each time, and then moves the last element to the top of the heap to adjust the heap. Each time only O(logn ) Level of time complexity, complete sorting n times is O(nlogn), but we only need k times each time, so it takes O(klogn) time complexity to complete the sorting function of k elements, and the entire time complexity is O (n+klogn) Because it is different from the previous one, it will not be merged.

I drew a picture to help everyone understand. If you do it twice, you will get Top2, and if you do it k times, you will get TopK.

The implementation code is:

class Solution {
    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    //下移交换 把当前节点有效变换成一个堆(大根)
    public void shiftDown(int arr[],int index,int len)//0 号位置不用
    {
        int leftchild=index*2+1;//左孩子
        int rightchild=index*2+2;//右孩子
        if(leftchild>=len)
            return;
        else if(rightchild<len&&arr[rightchild]>arr[index]&&arr[rightchild]>arr[leftchild])//右孩子在范围内并且应该交换
        {
            swap(arr, index, rightchild);//交换节点值
            shiftDown(arr, rightchild, len);//可能会对孩子节点的堆有影响，向下重构
        }
        else if(arr[leftchild]>arr[index])//交换左孩子
        {
            swap(arr, index, leftchild);
            shiftDown(arr, leftchild, len);
        }
    }
    //将数组创建成堆
    public void creatHeap(int arr[])
    {
        for(int i=arr.length/2;i>=0;i--)
        {
            shiftDown(arr, i,arr.length);
        }
    }
    public int findKthLargest(int nums[],int k)
    {
        //step1建堆
        creatHeap(nums);
        //step2 进行k次取值建堆，每次取堆顶元素放到末尾
        for(int i=0;i<k;i++)
        {
            int team=nums[0];
            nums[0]=nums[nums.length-1-i];//删除堆顶元素，将末尾元素放到堆顶
            nums[nums.length-1-i]=team;
            shiftDown(nums, 0, nums.length-i-1);//将这个堆调整为合法的大根堆，注意(逻辑上的)长度有变化
        }
        return nums[nums.length-k];
    }
}

Based on fast queue optimization

The above heap sort can be optimized, so what about fast sorting?

Of course, fast sorting is possible. How can I get fast sorting without such an amazing thing?

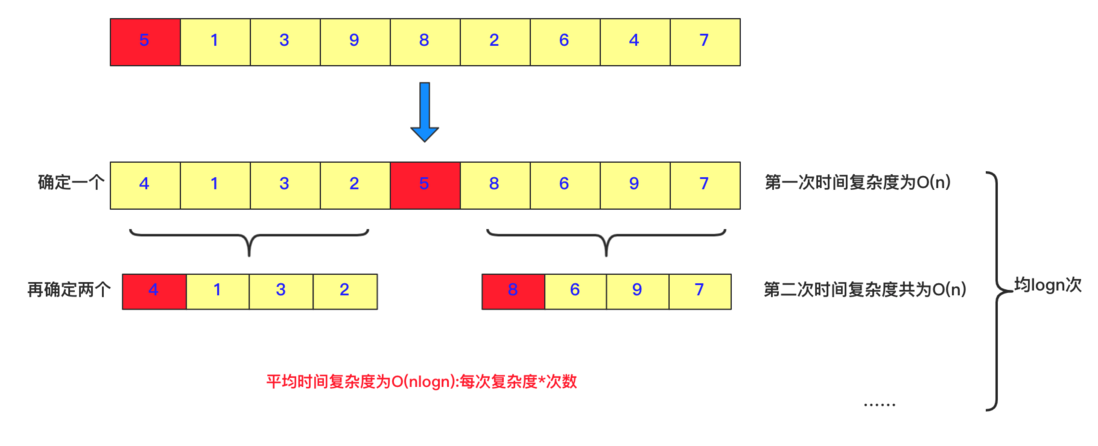
This part requires a certain understanding and understanding of heap and fast row. I wrote it a long time ago: illustrates hand-tear bubbling and fast row (to be optimized later). The core idea of fast row is: divide and conquer , determine one at a time The position of the number, and then the number is divided into two parts, the left side is smaller than it, and the right side is larger than it, and then this process is called recursively. The time complexity of each adjustment is O(n), and the average number of times is logn, so the average time complexity is O(nlogn).

But what does this have to do with seeking TopK?

When we ask for TopK, we actually ask for K that is larger than the target number. We randomly select a number such as 5 above. There are 4 on the left side of 5 and 4 on the right side. The following situations may occur:

① If k-1 is equal to the number on the right side of 5, then the 5 in the middle is the Kth, and it and its right side are both TopK.

② If k-1 is less than 5 , the number 161bac7e364dcd on the right side of , then TopK is all on the right side of 5, then you can directly compress the space to the right side and continue to call the same method to search recursively.

③ If k-1 is greater than the number on the right side of 5, it means that the right side and 5 are all in TopK, and then there is still on the left side ( on the right side of 5), and the search range is compressed. k is also compressed. For example, if k=7 then 5 and 5 have already accounted for 5 numbers on the right side and must be in Top7. We only need to find Top2 on the left side of 5.

In this way, the value will be compressed every time, because the fast sorting is not completely recursive, the time complexity is not O(nlogn) but O(n) level (for details, you can find some online proofs), but the test samples have some extreme codes For example, if you order 1 2 3 4 5 6 with you... Finding Top1 will lead to extreme situations. Therefore, a random number will be exchanged with the first one to prevent special examples (only for the purpose of brushing the questions). Of course, I will not add random exchanges here, and if the TopK to be obtained here is unsorted .

The detailed logic can be seen in the implementation code:

class Solution {
    public int findKthLargest(int[] nums, int k) {
        quickSort(nums,0,nums.length-1,k);
        return nums[nums.length-k];
    }
    private void quickSort(int[] nums,int start,int end,int k) {
        if(start>end)
            return;
        int left=start;
        int right=end;
        int number=nums[start];
        while (left<right){
            while (number<=nums[right]&&left<right){
                right--;
            }
            nums[left]=nums[right];
            while (number>=nums[left]&&left<right){
                left++;
            }
            nums[right]=nums[left];
        }
        nums[left]=number;
        int num=end-left+1;
        if(num==k)//找到k就终止
            return;
        if(num>k){
            quickSort(nums,left+1,end,k);
        }else {
            quickSort(nums,start,left-1,k-num);
        }
    }
}

Counting and Sorting Extra

Sorting always has some sorting of Sao operations—linear sorting, so you might ask whether bucket sorting is OK?

It's okay, but it depends on the value range for optimization. Bucket sorting is suitable for the situation where there are more occurrences of data evenly and densely, and counting sorting hopes that the value can be smaller.

So what is the specific core idea of using bucket sorting?

First use counting sorting to count the number of occurrences of each number, and then add a new array from the back to the front to add and calculate the sum.

This situation is ideal for value massive and small distribution case.

I did not want to write the code, but thought you would give me three even I write about it

//力扣215
//1 <= k <= nums.length <= 104
//-104 <= nums[i] <= 104
public int findKthLargest(int nums[],int k)
{
  int arr[]=new int[20001];
  int sum[]=new int[20001];

  for(int num:nums){
    arr[num+10000]++;
  }
  for(int i=20000-1;i>=0;i--){
    sum[i]+=sum[i+1]+arr[i];
    if(sum[i]>=k)
      return i-10000;
  }
  return 0;
}

Concluding remarks

Alright, today's TopK problem ends here, I believe you will definitely handle it next time you encounter it.

The TopK problem is not difficult, it's just a clever use of sorting. Sorting is very important, and interviews are very frequent.

Here I will not hide the showdown, how will I guide you to talk about TOPK from the perspective of the interviewer.

Cunning interviewer:

Well, let's talk about data structure and algorithm, let's talk about sorting, you should have been exposed to it? Tell me about the three sorting methods you are most familiar with, and explain the specific algorithm methods among them.

Humble me:

bia la bia la bia la bia la……

If you mentioned fast sorting, bucket sorting might let you use this sorting to implement TopK problems, other sorts are also possible, so it is very necessary to master the top ten sorts!

First public bigsai : 061bac7e365025, please attach the link to this article for reprinting, the original is not easy, please like and follow, thank you!