Preparing for the 2022 Spring Recruitment, these ten questions are bound to come!

Hi everyone, my name is bigsai.

Recently, many friends have communicated with me about the problem of swelling. The suggestion I gave is to point to the offer and force the hot100. There are also some of these questions that are very important and frequently appearing. Today I will share with you today. The 10 most frequently occurring algorithmic questions are earned by learning.

0X01 flip linked list

The original question of Likou 206 and Jianzhi offer24, which means:

Give you the head node head singly linked list, please reverse the linked list and return the reversed linked list.

analysis:

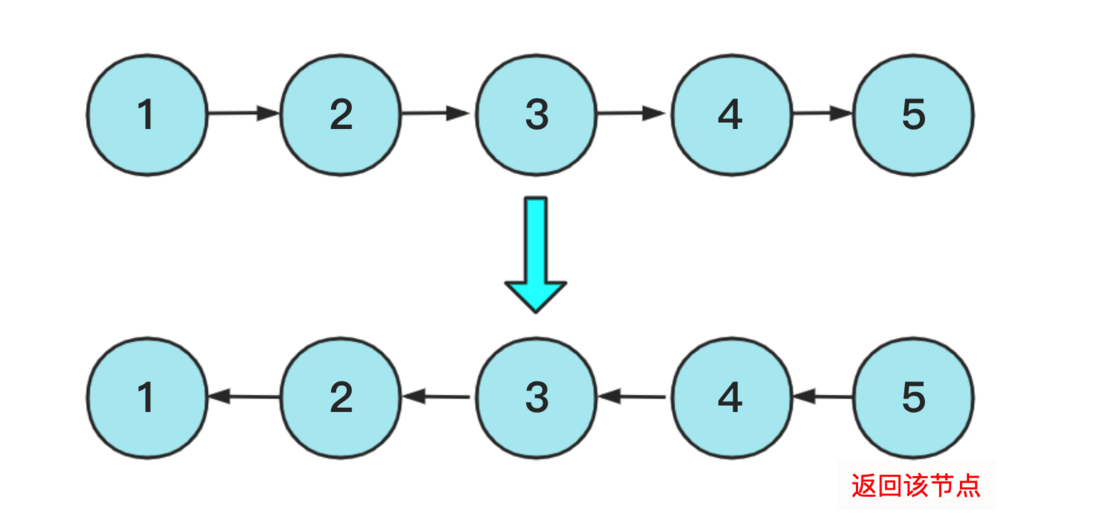
Flip the linked list, the original intention is not to create a new linked list node and then realize the flip on the original linked list, but this picture is a bit misleading, in fact, you can see the following picture for a better understanding:

The specific implementation of the above two ideas, non-recursive and recursive implementation methods, non-recursive implementation is relatively simple, use a pre node to record the predecessor node, and change the pointer point when enumerating downwards. The implementation code is:

class Solution {
    public ListNode reverseList(ListNode head) {
       if(head==null||head.next==null)//如果节点为NULL或者单个节点直接返回
            return head;
        ListNode pre=head;//前驱节点
        ListNode cur=head.next;//当前节点用来枚举
        while (cur!=null)
        {
            ListNode next=cur.next;
            //改变指向
            cur.next=pre;
            pre=cur;
            cur=next;
        }
        head.next=null;//将原先的head节点next置null防止最后成环
        return pre;
    }
}

The recursion method is more clever. With the help of the process of recursion, the pointer pointing and the return value transfer are cleverly changed. Although the code is simplified, it is difficult to understand. Here is a picture to help everyone understand:

The specific code is:

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null||head.next==null)//如果最后一个节点不操作
            return  head;
        ListNode node =reverseList(head.next);//先递归 到最底层 然后返回
        head.next.next=head;//后面一个节点指向自己
        head.next=null;//自己本来指向的next置为null
        return node;//返回最后一个节点(一直被递归传递)
    }
}

0X02 Design LRU

For the stress deduction 146LRU cache mechanism, the subject requirements are:

Use the data structure you have mastered to design and implement an LRU caching mechanism. Implement the LRUCache class:

LRUCache(int capacity) initializes the LRU cache with a positive integer as the capacity capacity
int get(int key) If the key exists in the cache, return the value of the key, otherwise return -1.
void put(int key, int value) If the keyword already exists, change its data value; if the keyword does not exist, insert the group "key-value". When the cache capacity reaches the upper limit, it should delete the oldest unused data value before writing new data to make room for the new data value.

advanced : complete these two operations in O(1) time complexity

detailed analysis : once fell on the LRU experience

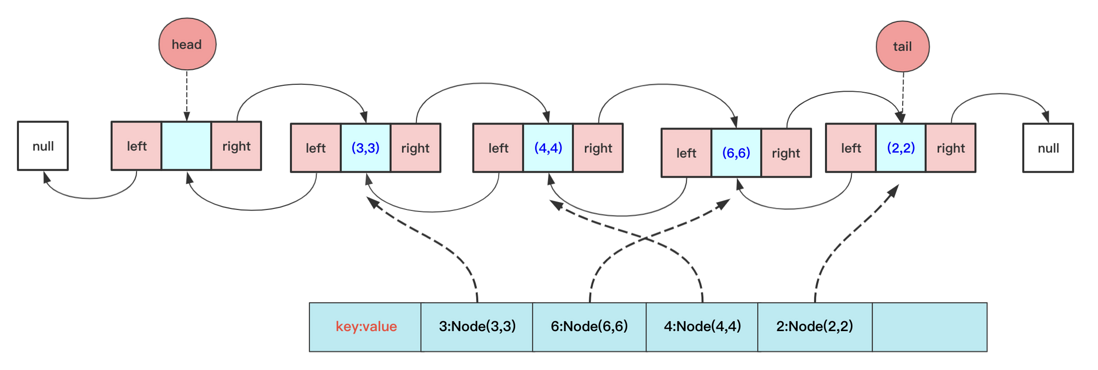
The core of LRU is to use hash + double-linked list , hash is used for query, double-linked list is deleted only know that the current node can also be deleted with O(1) complexity, but double-linked list needs to consider the special case of head and tail pointers.

The specific implementation code is:

class LRUCache {
    class Node {
        int key;
        int value;
        Node pre;
        Node next;
        public Node() {
        }
        public Node( int key,int value) {
            this.key = key;
            this.value=value;
        }
    }
    class DoubleList{
        private Node head;// 头节点
        private Node tail;// 尾节点
        private int length;
        public DoubleList() {
            head = new Node(-1,-1);
            tail = head;
            length = 0;
        }
        void add(Node teamNode)// 默认尾节点插入
        {
            tail.next = teamNode;
            teamNode.pre=tail;
            tail = teamNode;
            length++;
        }
        void deleteFirst(){
            if(head.next==null)
                return;
            if(head.next==tail)//如果删除的那个刚好是tail  注意啦 tail指针前面移动
                tail=head;
            head.next=head.next.next;

            if(head.next!=null)
                head.next.pre=head;
            length--;
        }
        void deleteNode(Node team){

            team.pre.next=team.next;
            if(team.next!=null)
                team.next.pre=team.pre;
            if(team==tail)
                tail=tail.pre;
           team.pre=null;
           team.next=null;
            length--;
        }
    }
    Map<Integer,Node> map=new HashMap<>();
    DoubleList doubleList;//存储顺序
    int maxSize;
    LinkedList<Integer>list2=new LinkedList<>();

    public   LRUCache(int capacity) {
        doubleList=new DoubleList();
        maxSize=capacity;
    }
    public int get(int key) {
        int val;
        if(!map.containsKey(key))
            return  -1;
        val=map.get(key).value;
        Node team=map.get(key);
        doubleList.deleteNode(team);
        doubleList.add(team);
        return  val;
    }

    public void put(int key, int value) {
        if(map.containsKey(key)){// 已经有这个key 不考虑长短直接删除然后更新
           Node deleteNode=map.get(key);
            doubleList.deleteNode(deleteNode);
        }
        else if(doubleList.length==maxSize){//不包含并且长度小于
            Node first=doubleList.head.next;
            map.remove(first.key);
            doubleList.deleteFirst();
        }
       Node node=new Node(key,value);
        doubleList.add(node);
        map.put(key,node);

    }
}

0X03 circular linked list

For the stress buckle 141 and the force buckle 142, the requirements of the force buckle 141 ring chain watch are:

Given a linked list, judge whether there is a ring in the linked list, and solve it with O(1) memory.

detailed analysis : circular linked list to find the entrance, really wonderful

This problem is more efficient by using fast and slow dual pointers. Fast pointer takes 2 steps each time, slow takes 1 step each time, and slow pointer takes n steps to the end. The fast pointer takes 2n steps, and the size of the ring must be less than or equal to n, so it must be Will meet, if you meet, then it means there is a ring, if you don’t meet, fast is null first, it means there is no ring.

The specific code is:

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast=head;
        ListNode slow=fast;
        while (fast!=null&&fast.next!=null) {
            slow=slow.next;
            fast=fast.next.next;
            if(fast==slow)
                return true;
        }
        return false;    
    }
}

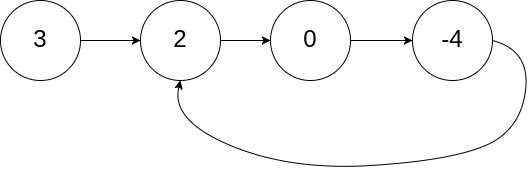
Likou 142 is expanded in Likou 141. If there is a loop, return to the node where it entered the loop, and I would like to return to node 2 in the circular linked list shown in the figure below.

This problem requires mathematical conversion. For specific analysis, please refer to the detailed analysis above. Here, I will mention the steps of the big problem.

If the first intersection is found, one of stops, the other continues to , and the next time the intersection happens to go one circle, the length of the loop part of .

So what we know is: fast takes 2x steps, slow takes x steps, and the ring length is y. And when the fast pointer and the slow pointer converge, the is just an integer multiple of the length y (the two are in the same position at the moment, and the fast pointer has exactly the same number of turns to gather at the same position), You can get 2x=x+ny (x=ny). Among them, it is said that the x of the slow pointer and the x of the fast pointer are integer multiples of the circle length y.

That is to say, from the beginning to this point in total x steps, from this point to walk x steps is to go around a few times and return to this point . If slow starts from the starting point and fast starts from this point (one step at a time, which is equivalent to offsetting the distance traveled by slow in the previous two steps), then walking x steps will reach this point, but the two pointers Each time you take one step, so once the slow reaches the loop, the two pointers start to converge .

The implementation code is:

public class Solution {
    public ListNode detectCycle(ListNode head) {
        boolean isloop=false;
        ListNode fast=new ListNode(0);//头指针
        ListNode slow=fast;
        fast.next=head;
        if(fast.next==null||fast.next.next==null)
            return null;
        while (fast!=null&&fast.next!=null) {
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow)
            {
                isloop=true;
                break;
            }
        }
        if(!isloop)//如果没有环返回
            return null;
        ListNode team=new ListNode(-1);//头指针 下一个才是head
        team.next=head;
        while (team!=fast) {//slow 和fast 分别从起点和当前点出发
            team=team.next;
            fast=fast.next;
        }
        return team;
    }
}

0X04 two stacks to achieve queue

Corresponding to offer09, the title means:

Implement a queue with two stacks. The declaration of the queue is as follows. Please implement its two functions appendTail and deleteHead, which respectively complete the functions of inserting integers at the end of the queue and deleting integers at the head of the queue. (If there is no element in the queue, the deleteHead operation returns -1)

analyzes :

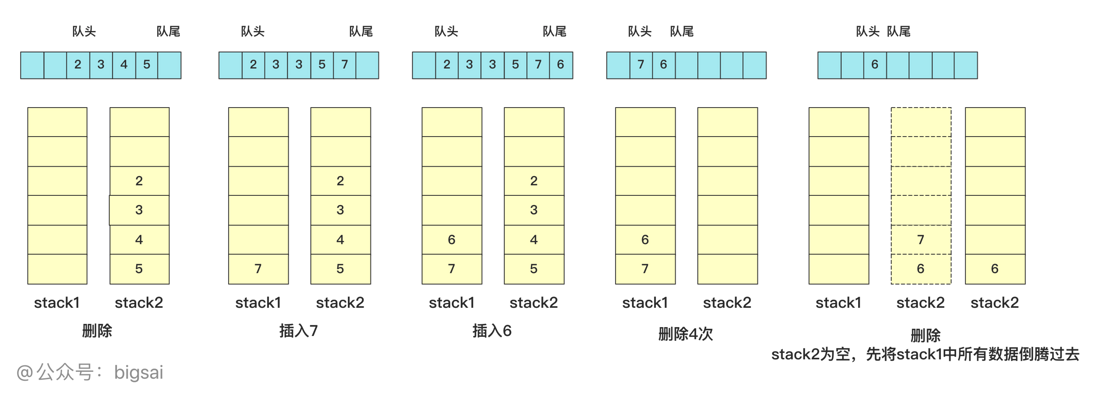
To solve this problem, you need to know what the stack is and what the queue is. The two common data structure formats are very simple. The characteristics of the stack are: last-in, first-out , the characteristics of the queue are: first-in , the stack can be imagined as a stack For books, the earlier you get the book, the earlier you get from (for analogy) ; the queue is like queuing to buy things, only in and comes out , so the data structure of the two is still different, although They are all in and out of a single entry, but the stack entry and exit are the same, but the queues are different.

The data structure of a normal stack and queue is described above. Here, let us use two stacks to implement a queue operation. The easier solution here is that one of the stacks, stack1, is used as data storage, and it is directly inserted into stack1 at the end of the insertion. When deleting the header, add the data to another stack stack2 first, return and delete the top element of the stack, add stack2 to stack1 in order to achieve a restoration, but the operation insertion time complexity is O(1), and the deletion time complexity O(n) is relatively high.

The realization method is also shown for everyone:

class CQueue {

    Stack<Integer>stack1=new Stack<>();
    Stack<Integer>stack2=new Stack<>();
    public CQueue() {
    }
    public void appendTail(int value) {
       stack1.push(value);
    }
    public int deleteHead() {
        if(stack1.isEmpty())
            return -1;
       
        while (!stack1.isEmpty())
        {
            stack2.push(stack1.pop());
        }
       int value= stack2.pop();
        while (!stack2.isEmpty())
        {
            stack1.push(stack2.pop());
        }
        return  value;
    }
}

This kind of time complexity is not liked, because deletion is too time-consuming and has to be tossed every time. Is there any good way to make deletion easier?

Yes, stack1 can be inserted in order, and stack1 data can be inserted in stack2 to ensure order deletion, so uses stack1 for insertion and stack2 for deletion , because the title does not require the data to be placed in a container, so it is combined like this Use, perfect!

In the specific implementation, insert directly into stack1. If you need to delete it, delete it from the top of stack2. If stack2 is empty, add all the data in stack1 (this will ensure that all data in stack2 can be deleted sequentially ), here are a few examples of deletion

In fact, the data is divided into two parts, one part is used to insert, the other part is used to delete, and the deleted stack stack2 is empty, adding all the data in stack1 to continue the operation. The time complexity of insertion and deletion of this operation is O(1), and the specific implementation code is:

class CQueue {
    Deque<Integer> stack1;
    Deque<Integer> stack2;
    
    public CQueue() {
        stack1 = new LinkedList<Integer>();
        stack2 = new LinkedList<Integer>();
    }
    
    public void appendTail(int value) {
        stack1.push(value);
    }
    
    public int deleteHead() {
        // 如果第二个栈为空 将stack1数据加入stack2
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        } //如果stack2依然为空 说明没有数据
        if (stack2.isEmpty()) {
            return -1;
        } else {//否则删除
            int deleteItem = stack2.pop();
            return deleteItem;
        }
    }
}

0X05 Binary tree sequence (sawtooth) traversal

The traversal of the binary tree, the stress button 102, 107, 103.

detailed analysis : interview, the binary tree traversal sequence off the hook

If the ordinary binary tree is traversed in sequence, it is not a difficult problem, but it will have an operation to return the result hierarchically, which requires you to consider in detail.

Many people use two containers (queues) for layered operations. In fact, one queue can be used directly. We first record the queue size len before enumeration, and then enumerate and traverse according to this size len to get the complete layer. Data.

Another difficulty is the zigzag layer sequence of the binary tree (also called zigzag printing). The first pass is from left to right, and the second pass is from right to left. You only need to record a number of odd and even layers for the corresponding operation. .

Here I take the zigzag sequence traversal of the Likou 103 binary tree as the question board to share with you the code:

public List<List<Integer>> levelOrder(TreeNode root) {
  List<List<Integer>> value=new ArrayList<>();//存储到的最终结果
  if(root==null)
    return value;
  int index=0;//判断
  Queue<TreeNode>queue=new ArrayDeque<>();
  queue.add(root);
  while (!queue.isEmpty()){
    List<Integer>va=new ArrayList<>();//临时 用于存储到value中
    int len=queue.size();//当前层节点的数量
    for(int i=0;i<len;i++){
      TreeNode node=queue.poll();
      if(index%2==0)//根据奇偶 选择添加策略
        va.add(node.val);
      else
        va.add(0,node.val);
      if(node.left!=null)
        queue.add(node.left);
      if(node.right!=null)
        queue.add(node.right);
    }
    value.add(va);
    index++;
  }
  return value;
}

0X06 Post-order traversal in binary tree (non-recursive)

The non-recursive traversal of the binary tree is also the focus of the investigation. The recursive implementation of the middle-order and post-order traversal is very simple, and the non-recursive implementation is still a trick.

Detailed analysis: Binary tree traversal (recursive, non-recursive)

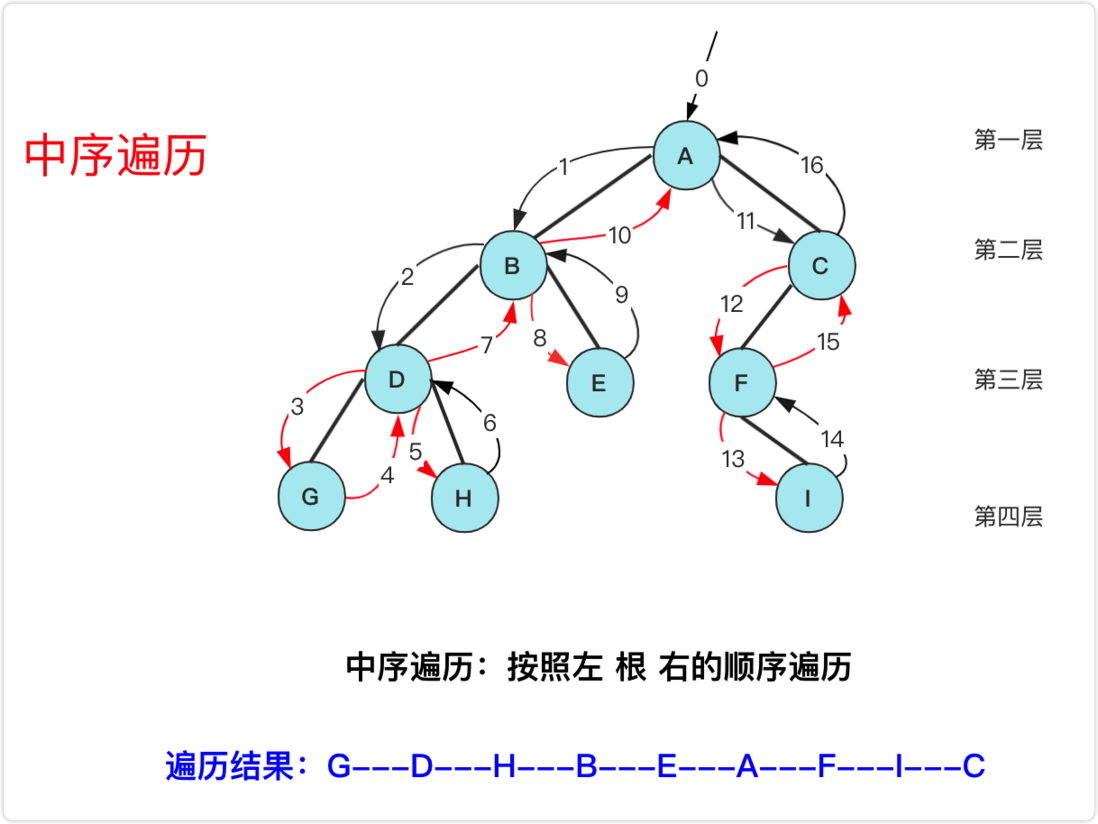
For the middle order traversal of the binary tree, in fact, the output is thrown when the node is accessed for the second time under normal circumstances (the first order is the first time), so that we can not delete each node for the first time enumerating, and we need to save it first To the stack, when the left child node is processed, it is thrown to visit the node.

The core is just two steps, the left and right leaf nodes are null, and the following conditions can also be met:

1. Enumerate the current node (do not store the output) and store it in the stack. The node points to the left node until the left child is null.
2. Throw the top of the stack to visit. If there is a right node, visit its right node and repeat step 1. If there is no right node, continue to repeat step 2 to throw.

The implementation code is:

class Solution {
   public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer>value=new ArrayList<Integer>();
    Stack<TreeNode> q1 = new Stack();    
    while(!q1.isEmpty()||root!=null)
    {
        while (root!=null) {
            q1.push(root);                
            root=root.left;
        }
        root=q1.pop();//抛出
        value.add(root.val);
        root=root.right;//准备访问其右节点
        
    }
    return value;
  }
}

The post-order traversal is actually based on the recursive idea. In fact, the third visit to the node is to throw the output after returning from the right child node. This is indeed difficult to implement. But for the specific implementation, we use a pre node to record the last access point that was thrown out. If currently being thrown is pre or the current node right is null , then this point is thrown, otherwise it means it The right side of has not been visited yet, it needs to be "rebuilt" and used later! If you don't understand, you can see the detailed introduction above.

The specific implementation code is:

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        TreeNode temp=root;//枚举的临时节点
        List<Integer>value=new ArrayList<>();
        TreeNode pre=null;//前置节点
        Stack<TreeNode>stack=new Stack<>();

        while (!stack.isEmpty()||temp!=null){
        
            while(temp!=null){
                stack.push(temp);
                temp=temp.left;
            }
            temp=stack.pop();
            if(temp.right==pre||temp.right==null)//需要弹出
            {
                value.add(temp.val);
                pre=temp;
                temp=null;//需要重新从栈中抛出
            }else{
                stack.push(temp);
                temp=temp.right;
            }
            
        }
        return value;
    }
}

Of course, the post-order traversal also uses the pre-order ( root right-left ) the result of the pre-order traversal is finally flipped, but the interviewer wants to investigate the method mentioned above.

0X07 Jumping stairs (Fibonacci, climbing stairs)

Climbing stairs and jumping stairs is a classic problem, corresponding to Jianzhi offer10 and Likou 70 questions. The requirements for the questions are:

Suppose you are climbing stairs. You need n to reach the top of the building. You can climb 1 or 2 steps each time. How many different ways do you have to climb to the top of a building? Note: gives n is a positive integer.

analysis:

The entry level dp of this question, analyze the results of the current k-th step, everyone can climb 1 or 2 steps, then it means that it may come from k-1 or k-2, so it is the superposition of the two sub-cases (requires Consider the initial situation in particular). Some people think of this idea of recursion. Yes, it can be solved by recursion, but the efficiency of recursion is lower (because this is a divergent recursion and one is split into two). Memoized search will be slightly better.

But dp is a better method, the core state transition equation is: dp[i]=dp[i-1]+dp[i-2] , some space optimization is better, because only the first two values are used, so three values can be reused to save space.

class Solution {
    public int climbStairs(int n) {
        if(n<3)return n;
         int dp[]=new int[n+1];
         dp[1]=1;
         dp[2]=2;
         for(int i=3;i<n+1;i++)
         {
             dp[i]=dp[i-1]+dp[i-2];
         }
         return dp[n];
    }
  
  public int climbStairs(int n) {
        int a = 0, b = 0, c = 1;
        for (int i = 1; i <= n; i++) {
            a = b; 
            b = c; 
            c = a + b;
        }
        return c;
    }
}

Of course, some data is very large, and you can use the matrix to solve it quickly. But I won't introduce it here. If you are interested, you can take a look at it in detail.

0X08 TOPK problem

The TOPK question is really classic. Usually the smallest number of K is asked, and the search for the Kth is mostly TOPK. Here, I will force 215 to find the Kth largest element of the array as the board.

Detailed analysis: is TOPK

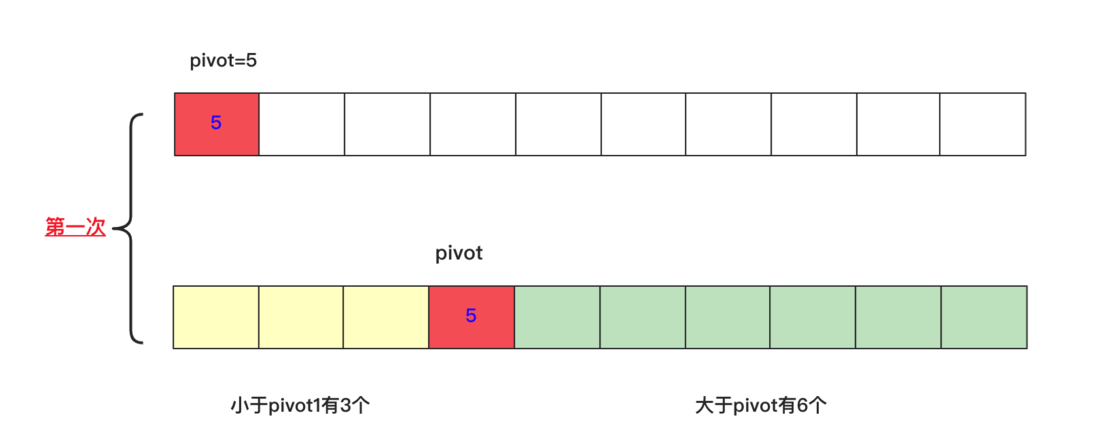
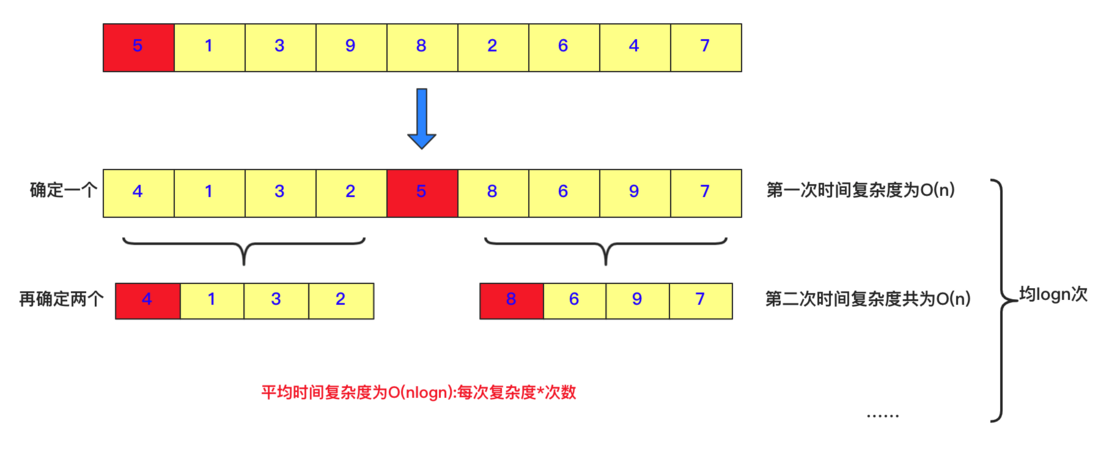
There are many ways to solve the problem of TOPK. If optimized bubbling or simple selection sorting, the time complexity is O(nk), and the optimized heap sorting is O(n+klogn), but the deformation of fast sorting can handle the general All the questions above (if the interviewer asks you to sort by hand, it would be a bit difficult for you).

Quick row determines a number pivot position each time, and divides the number into two parts: the left side is smaller than this number pivot, and the right side is larger than this number pivot, so that you can judge whether it is just at the pivot position or the left side according to this k Or the right side? You can compress the space iteration to call recursion and finally find the result.

Many people choose the pivot not to choose the first one randomly in order to pass the test sample faster (to fight against the tricky test sample), but here I choose the first one as the pivot, the code can refer to:

class Solution {
    public int findKthLargest(int[] nums, int k) {
        quickSort(nums,0,nums.length-1,k);
        return nums[nums.length-k];
    }
    private void quickSort(int[] nums,int start,int end,int k) {
        if(start>end)
            return;
        int left=start;
        int right=end;
        int number=nums[start];
        while (left<right){
            while (number<=nums[right]&&left<right){
                right--;
            }
            nums[left]=nums[right];
            while (number>=nums[left]&&left<right){
                left++;
            }
            nums[right]=nums[left];
        }
        nums[left]=number;
        int num=end-left+1;
        if(num==k)//找到k就终止
            return;
        if(num>k){
            quickSort(nums,left+1,end,k);
        }else {
            quickSort(nums,start,left-1,k-num);
        }
    }
}

0X09 The longest substring without repetition (array)

This problem may be a string may also be an array, but the same truth, no repetitive characters the longest substring and longest non-repeating sub-arrays consistent nature.

The subject requirement is: Given a string, please find out the length of the longest substring that does not contain repeated characters.

analysis :

This question is to give a string to let you find the longest substring without repetition. To find out the difference between the substring and the subsequence

substring : It is continuous and can be regarded as a part of the original string.
subsequence : It is not necessarily continuous, but the relative position of each element must be kept unchanged.

So how do we deal with it?

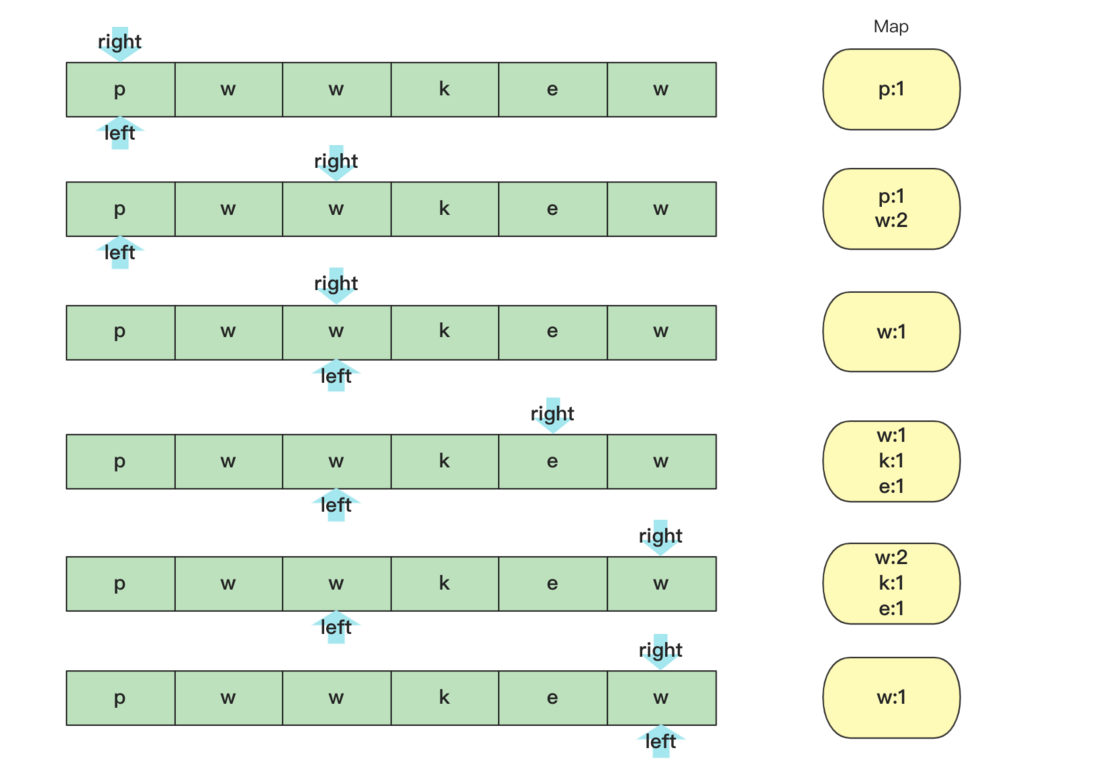
Brute force search, brute force search is of course possible, but if the complexity is too high, I won't explain it here. The idea of choice here is sliding window, sliding window is to use an interval from left to right, the right side of , and the maximum value of the interval without repetition is found. When there is repetition, the left side moves to the right side until there is no repetition , And then repeat to the end. Just find the largest substring in the whole process.

In specific implementation, you can use an array to replace the hash table, which will be much faster:

class Solution {
    public int lengthOfLongestSubstring(String s) {
         int a[]=new int[128];
         int max=0;//记录最大
         int l=0;//left 用i 当成right，当有重复左就往右
         for(int i=0;i<s.length();i++)
         {
             a[s.charAt(i)]++;
             while (a[s.charAt(i)]>1) {
                a[s.charAt(l++)]--;
            }
             if(i-l+1>max)
                 max=i-l+1;
         }
         return max;
    }
}

0X10 sort

No one really thinks that using Arrays.sort() is enough. Handwritten sorting is still very high-frequency. Simple things like bubbling and inserting are compared to others, such as heap sorting, hill sorting, radix sorting, etc. Not much. Comparing the is the fast sorting . Here is an extra bonus for a merge sort that is also very high-frequency. Both are typical divide and conquer algorithms. You can also compare the fast sorting with the previous TOPK problem.

The top ten sorts of sorts have been detail, you can refer to them yourself: 161c97d4be7ab9 Programmers must know the top ten sorts

Fast queue:

Implementation:

public void quicksort(int [] a,int left,int right)
{
  int low=left;
  int high=right;
  //下面两句的顺序一定不能混，否则会产生数组越界！！！very important！！！
  if(low>high)//作为判断是否截止条件
    return;
  int k=a[low];//额外空间k，取最左侧的一个作为衡量，最后要求左侧都比它小，右侧都比它大。
  while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
  {
    while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
    {
      high--;
    }
    //这样就找到第一个比它小的了
    a[low]=a[high];//放到low位置
    while(low<high&&a[low]<=k)//在low往右找到第一个大于k的，放到右侧a[high]位置
    {
      low++;
    }
    a[high]=a[low];            
  }
  a[low]=k;//赋值然后左右递归分治求之
  quicksort(a, left, low-1);
  quicksort(a, low+1, right);        
}

Merge sort:

The implementation code is:

private static void mergesort(int[] array, int left, int right) {
  int mid=(left+right)/2;
  if(left<right)
  {
    mergesort(array, left, mid);
    mergesort(array, mid+1, right);
    merge(array, left,mid, right);
  }
}

private static void merge(int[] array, int l, int mid, int r) {
  int lindex=l;int rindex=mid+1;
  int team[]=new int[r-l+1];
  int teamindex=0;
  while (lindex<=mid&&rindex<=r) {//先左右比较合并
    if(array[lindex]<=array[rindex])
    {
      team[teamindex++]=array[lindex++];
    }
    else {                
      team[teamindex++]=array[rindex++];
    }
  }
  while(lindex<=mid)//当一个越界后剩余按序列添加即可
  {
    team[teamindex++]=array[lindex++];

  }
  while(rindex<=r)
  {
    team[teamindex++]=array[rindex++];
  }    
  for(int i=0;i<teamindex;i++)
  {
    array[l+i]=team[i];
  }
}

Concluding remarks

Well, the 10 questions I shared with you today are really very, very high-frequency in interviews. I dare to say that on average, I have to encounter one of these questions every two interviews (no exaggeration)!

Although the question sea is very in-depth study, but those who have learned to cache all know that hot data should be cached, and those who have taken the test know that they must master the required test points... These ten questions have been brought to the mouth.

Of course, this is only a very, very high-frequency problem. If you want to grasp the written test, you must continue to accumulate and questions. You are also welcome to join my 161c97d4be7c17 punch card group and insist on questions 161c97d4be7c1a!

Originality is not easy, ask for a triple match!

bigsai personal technical public number "061c97d4be7c70", please attach the author and the link to this article for reprinting.