Randomly sample a certain amount of data from the dataset

Turning to a previously answered question today: Randomly draw a certain amount of data from a list. The previous answer was solved using the Fisher-Yates shuffling algorithm, but after reading the comments, some new ideas.

Let's not talk about the algorithm first, just talk about the idea of random extraction.

Algorithm Evolution of Random Draw

Assuming that there are n pieces of data stored in a list source (array in JavaScript), m (m <= n) pieces of data need to be randomly selected, and the result is placed in another list result . Since random extraction is a repetitive process, it can be completed by a loop of m times. In the loop body, one number is selected from source each time (find it and delete it from source ), and put it in result in turn. Described in JavaScript is

function randomSelect(source, m) {
    const result = [];
    for (let i = 0; i < m; i++) {
        const rIndex = ~~(Math.random() * source.length);
        result.push(source[rIndex]);
        source.splice(rIndex, 1);
    }
    return result;
}

In most languages, deleting a piece of data from the middle of the list will cause subsequent data rearrangement, which is an inefficient operation. Considering that randomly selecting an event from a set of data is an equal probability event, it has nothing to do with the location of the data, we can remove the selected data, instead of reducing the length of the list, directly move the last data in the list. The last element is not taken into account when the next random location is taken. This improved algorithm:

function randomSelect(source, m) {
    const result = [];
    for (let i = 0, n = source.length; i < m; i++, n--) {
//                  ^^^^^^^^^^^^^^^^^              ^^^
        const rIndex = ~~(Math.random() * n);
        result.push(source[rIndex]);
        source[rIndex] = source[n - 1];
//      ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
    }
    return result;
}

Note that n-- and n - 1 can be merged here, after merging:

for (let i = 0, n = source.length; i < m; i++) {
    ...
    source[rIndex] = source[--n];
}

At this time, I noticed again that the unused space behind source is actually the same size as the space of result . If this part of the space is used, result is no longer needed.

function randomSelect(source, m) {
    for (let i = 0, n = source.length; i < m; i++) {
        const rIndex = ~~(Math.random() * n);
        --n;
        // 交换选中位置的数据和当前最后一个位置的数据
        [source[rIndex], source[n]] = [source[n], source[rIndex]];
    }
    // 把后面 m 个数据返回出来就是随机选中的
    return source.slice(-m);  // -m 和 source.length - m 等效
}

If you keep the original result and related algorithms, you will find that result and the returned array elements are arranged in reverse order. But it doesn't matter, because our purpose is to choose randomly, whether revert or not, the result set is random.

But this way, let's say m = source.length , the entire data in source is randomly arranged - this is Fisher-Yates algorithm . Of course, in fact, only source.length - 1 processing is required to achieve the effect of complete shuffling.

Fisher-Yates shuffle algorithm

Fisher-Yates efficient and equal-probability shuffling algorithm. The core idea is to randomly extract a number from 1 to n and exchange it with the last number (n), and then randomly select a number from 1 to n-1 and exchange it with the penultimate number (n-1)… ..., after n - 1 rounds, the data in the original list is completely randomly shuffled.

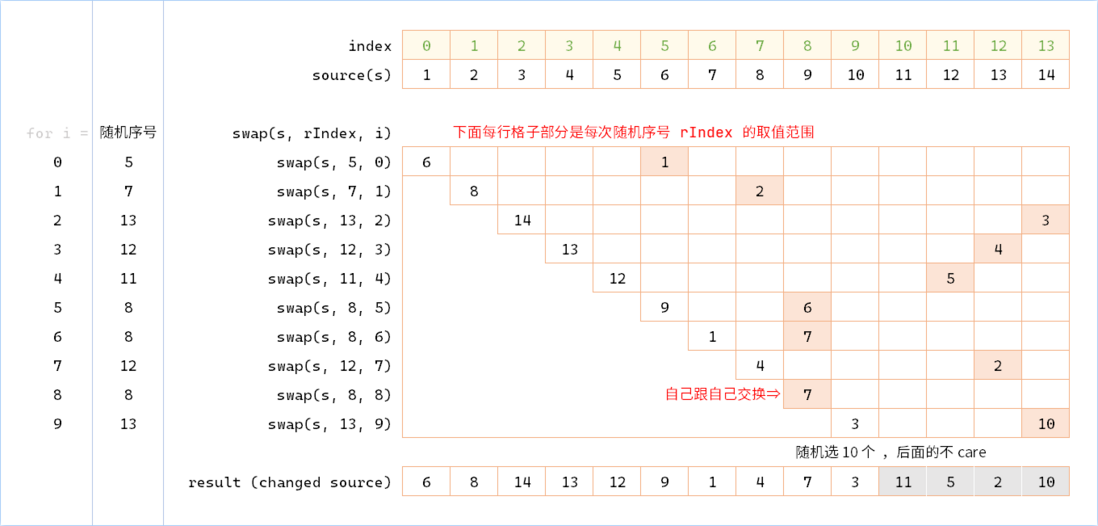
Each time it is swapped with the "current last element", the processing result is appended. If you change each time with the current position (ie i position) element exchange, you can prepend the result set. But it should be noted that the selection of random numbers is not the range of [0, n) (0 < n < source.length) , but the range of [i, source.length) :

function randomSelect(source, m) {
    for (let i = 0, n = source.length; i < m; i++, n--) {
        const rIndex = ~~(Math.random() * n) + i;
        [source[rIndex], source[i]] = [source[i], source[rIndex]];
    }
    return source.slice(0, m);
}

This process can be understood with a diagram (10 randomly selected)

Since it is a shuffling algorithm, in the case of a small amount of data, a ready-made tool function can be used to shuffle the cards and then extract continuous data of a specified size to achieve the purpose of random extraction. For example, use the method 16232951b1e81b of _.shuffle() .

import _ from "lodash";
const m = 10;
const result = _.shuffle(data).slice(0, m);

There are two problems here

• If the amount of original data is large, or the amount of original data is quite different from the amount of data to be extracted, a lot of computing power will be wasted
• The shuffling algorithm modifies the order of elements in the original dataset

For the first question, just use the randomSelect() manually typed earlier, and the second question will be discussed below.

Improve, do not modify the original data set

To not change the original data, that is, do not exchange or shift the elements in the data source. But need to know which data has been selected, what should we do? There are several methods

• Add a set of selected element serial numbers. If the calculated rIndex can be found in this set, select it again.

  This is a method, but as the ratio of optional sequence numbers to non-selectable sequence numbers gradually decreases, the probability of reselection will greatly increase, and the efficiency of the entire algorithm cannot be guaranteed at all.

• Also use a selected sequence number set according to the above method, but when a collision occurs, the sequence number is not reselected, but the sequence number is accumulated and modulo.
  This method is a bit more stable than the previous one, but still suffers from less stable accumulation calculations and may reduce randomness.
• ……

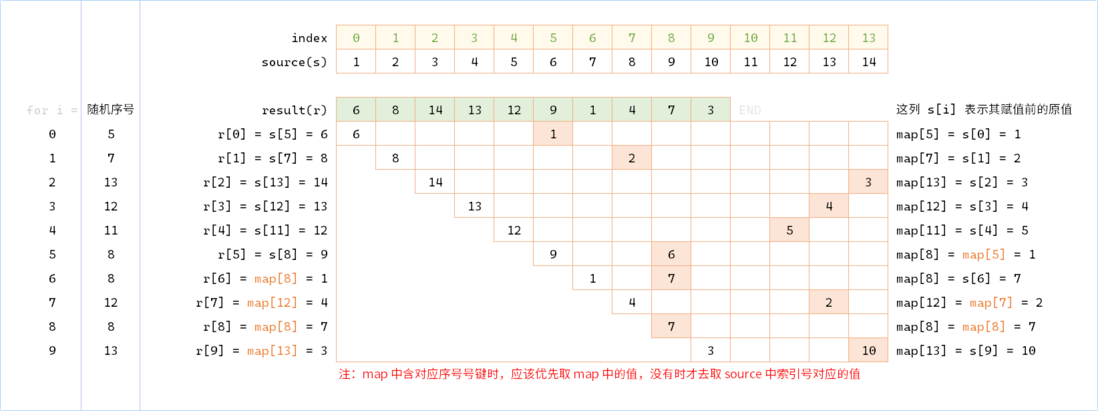
Thinking about it, the purpose of exchanging the last unused element with the element where rIndex is located is to make rIndex hit an unacquired value when it reappears - assuming that this value is not taken from the original data set, but Is it taken from an additional dataset?

For example, in the case of 6 , rIndex = 5 is taken for the first time to get source[5] . At this time, the last value should be assigned, which is source[5] = source[13] = 14 . We change this assignment process to map[5] = source[13] = 14 ; the next time we hit rIndex = 5 , first check whether map exists in map[5] , and if so, use it instead of using the elements in source . To describe this general process in code is:

const n = 
const value = map[rIndex] ?? source[rIndex];
result.push(value);  // 可以和上一句合并
map[rIndex] = map[n] ?? source[n];

The modified value corresponding to an index is stored in map , so every time you go to get the value in source , check map first. If there is in map , take the map in map source

It sounds more abstract, or the picture above

The corresponding code is also easy to write:

function randomSelect(source, m) {
    const result = [];
    const map = new Map();

    for (let i = 0, n = source.length; i < m; i++, n--) {
        const rIndex = ~~(Math.random() * n) + i;
        result[i] = map.get(rIndex) ?? source[rIndex];
//                  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
        map.set(rIndex, map.get(i) ?? source[i]);
//                      ^^^^^^^^^^^^^^^^^^^^^^^
    }

    return result;
}

Tip: This code can be compared with the last randomeSelect code in the previous section.