Explain the PID algorithm in simple terms

foreword

The blogger is an industrial Internet programmer. Although he is not an algorithm engineer or automation engineer, he often participates in the training of colleagues to introduce the principles of control algorithms, and gradually has a certain understanding of a small number of control algorithms, among which the most frequently used control algorithms are used. None other than PID. When many students learn PID, they will be intimidated by complicated mathematical formulas. Today, we will put aside the mathematical formulas and use logic and examples to explain to everyone "what is PID?"

Introduction to PID Algorithm

PID is a control algorithm, which is the abbreviation of Proportional (proportional), Integral (integral), and Differential (differential). It is the most mature and widely used control algorithm in continuous systems.

PID controllers are mainly suitable for systems that are basically linear and whose dynamic characteristics do not change with time. Simply put: PID can basically come in handy when a physical quantity needs to be "stabilized".

Typical application scenarios of PID in industry are: temperature control, flow control, liquid level control, etc.

PID applications in life are also very common: pressure control of tap water, temperature control of air conditioners, balance control of balance cars, cruise control of cars, hover control of drones, attitude adjustment of rocket planes, etc.

The actual operation experience and theoretical analysis show that the use of PID control algorithm to control many industrial processes can get relatively satisfactory results.

The concept and formula of PID

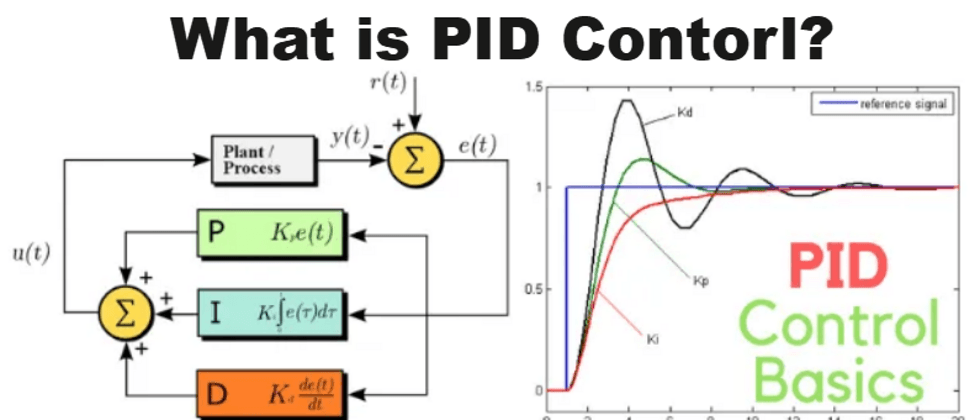
The basic idea of PID is to calculate a control value by using proportional, integral and differential according to the size of the deviation, and input this control value into the controlled system. After the system receives the input, it will output a corresponding output. PID control The controller detects the output again, calculates the deviation again, and then repeats the above process.

The original formula is as follows:
$u(t)=K_p \Bigg( e(t)+\frac{1}{T_i}\int^t_0e(t)dt+T_d\frac{de(t)}{dt}\Bigg)$

• $K_p$ —— the proportional coefficient of the controller;
• $T_i$ —— integral time constant;
• $T_d$ —— differential time constant;
• $u(t)$ —— output signal of PID controller;
• $e(t)$ - the difference between the given value $r(t)$ and the measured value.

The formula can be simplified to:
$u(t)=K_p * e(t) + K_i * \sum_{n=0}^te(t) + K_d * (e(t) - e(t-1))$

• $K_p$ —— the proportional coefficient of the controller;
• $K_i$ —— the integral coefficient of the controller;
• $K_d$ —— the differential coefficient of the controller;
• $u(t)$ —— output signal of PID controller;
• $e(t)$ - the difference between the given value $r(t)$ and the measured value.
• $e(t-1)$ —— The difference between the last given value $r(t)$ and the measured value.

Many students may be confused by the above mathematical formulas. It doesn't matter. Let's read the following examples first, and then look back at the formulas. I believe you can have a new understanding of the above formulas.

Before learning PID, we need to understand what is open-loop control and closed- loop control . These two concepts can help us better understand PID.

open loop control system

Open Loop Control System: A system that does not feed back the control results to affect the current control system. E.g:

• Switch - the moment after the switch is pressed, the control activity has ended, and whether the light is on has no effect on the activity of pressing the switch;
• Shooting - After the basketball is released, it can no longer be controlled. Regardless of whether the ball is scored or not, the control activity ends at the moment the ball is released.

closed loop control system

Closed Loop Control System: A system that needs to feed back the control results and compare them with desired values, and adjust the control action according to their errors. E.g:

• Adjust the faucet - first have a desired flow of water in the mind, after the faucet is opened, the existing flow is observed by eyes and compared with the expected value, and constantly adjusted by hand to form a feedback closed-loop control;
• Riding a bicycle - in the same way, it is necessary to continuously correct the direction and speed of travel to form a closed-loop control.

The closed-loop control system usually consists of the following six links.

Let's take "maintaining the water level of the tank at 1 meter" as an example to explain each link in the closed-loop control in detail:

• 传感器 : Manually measure the current water level
• 目标量 : Keep the tank water level at 1 meter
• 偏差量 : 目标量 - Current water level height
• 控制器 : Calculated according to 偏差量 执行量
• 执行量 : input parameter passed to 执行器
• 执行器 : Manually add water to the tank with a bucket

传感器 、 目标量 、 偏差量 、 执行量 、 执行器 5个环节都比较简单，一眼就Can understand the meaning. The most critical link 控制器 is relatively complicated. In the 控制器 link, different control algorithms are selected. According to the 偏差量 calculation 执行量 is also different. Today we will specifically look at the control effect of PID.

PID of 比例P

前面有说到PID的基本偏差量的大小， 比例P 、 积分I 、 微分D计算出一个控制量。 However, the three parameters of PID are not necessarily used together. You can use 比例P to control it, or you can use it in combination 比例P + 积分I 比例P + 微分D to control.

Let's first see what kind of control effects can be brought by using only 比例P ? Continuing the "water tank" example above:

• 传感器 : Manually measure the initial water level height of the tank is 0.2 meters
• 目标量 : Keep the tank water level at 1 meter
• 偏差量 : 1m - 0.2m = 0.8m
• 控制器 : Proportional control using PID algorithm, calculated according to 偏差量 执行量
• 执行量 : input parameter passed to 执行器
• 执行器 : Manually add water to the tank with a bucket

Usually the units between 偏差量 and 执行量 are different, in the current example 偏差量 has units of water tanks, while 执行量 It is a bucket, and their volumes are different, so we need a coefficient to enlarge or reduce the relationship between the two. The specific formula can be abstracted as:

执行量 = 比例P = 偏差量 * 比例P系数

At this time, suppose there is a person standing next to the water tank, adding water to the water tank with a bucket to control the height of the water level. If you simply use the proportional control algorithm, assuming 比例P系数 is 0.5 (equivalent to 两桶水的容量 equal to 一缸水的容量 ), we start to simulate the water addition experiment:

As shown in the results in the above figure, the water level of the tank can be increased to a height of 1 meter by manually adding water to the tank 8 times with a bucket. Convert the current water level into a curve, the approximate effect is as follows.

The above example is relatively simple, just relying 比例P can complete the task, but the reality is often only 比例P is not enough, let's look at a more complicated situation, suppose 比例P系数 is still 0.5, but the water tank will leak 0.1 meters of water between each addition of water. Let's simulate the water addition experiment from scratch and see what the specific results will be.

As shown in the results above, when the water level reaches 0.8, the water level will not continue to increase. Because, when the water level is equal to 0.8, 偏差量 is 0.2, and the amount of water added to the tank each time is 执行量 = 比例P = 0.2 * And every time the water is added, the water tank will leak water at a height of 0.1 meters, so the added water and the outflow water are offset.

Although the control system has reached a stable state at this time, there will be a stable difference between 实际值 and 目标量 , which is called 稳态误差 . 稳态误差 very common, such as: controlling the temperature of the air conditioner will cool down due to the air temperature difference, controlling the fixed height of the drone will fall down due to the influence of gravity, and controlling the cruise control of the car will have the influence of air resistance and friction While slowing down, these scenarios will generate 稳态误差 .

Only using 比例P to control the closed-loop loop cannot avoid the 稳态误差 problem, because 比例P系数 cannot be accumulated according to time or times, when there are external interference factors, 比例P系数 cannot be dynamically resized, then 稳态误差 will always exist.

If we introduce the dimension of time, we can get 2 artifacts 增幅器-积分I and 抑制器-微分D , they solve the case of 比例P 比例P too small and too large respectively, 比例P过小的话增幅器-积分I 稳态误差问题， 比例P过大由---67d4b312546f3badc814b1e3b0e04acd 抑制器-微分D .

PID of 积分I (amplifier)

Let's take a look at the amplifier 积分I , it can also be understood as accumulated experience, when 比例P is too small, it can be supplemented by 积分I , its principle is to use The elapsed time keeps adding up. The specific formula can be abstracted as:

比例P = 偏差量 * 比例P系数
积分I = 上一次积分I + 偏差量 * 积分I系数
执行量 = 比例P + 积分I

Imagine, if only 比例P control exists 稳态误差 , indicating 比例P 积分I Large value, to supplement 比例P , thus affecting 执行量 .

If the final control effect is jittering around 目标量 , we can get a positive and negative alternating 偏差量 , which will continuously generate positive and negative numbers near the target and accumulate to 积分I , 积分I will continue to approach zero, and eventually the control effect will become stable.

We continue to use the above example of "adding water to a water tank", assuming that 目标量 is 1, each leak is 0.1, 比例P系数 is 0.5, 积分I系数 --- is 0.5, and we then The water addition experiment was simulated from scratch, and the specific values are as follows.

Convert the current water level into a curve, the approximate effect is as follows.

The last round of experiments only used 比例P control presence 稳态误差 . 积分I 517099cb16e1857b22a91d7fb1ed1a6c---之后就有了累加效果，在未达到控制效果之前积分I 231e9d1a19281b17dac6cbaaf448c0da---会持续累加，在目标量 积分I Because inertia will continue to over-control, at the same time 偏差量 will turn from positive to negative and then positive, 积分I will also turn from positive to negative and then positive, and finally 积分I It will continue to offset each leak by 0.1, and the control effect tends to be stable.

Amplifiers have their own dangers. If there is an accident or error in the system, the amplifiers may be accumulated to infinity, making the system unusable, so the amplifiers need to have certain restrictions.

• 1. Limit the range, set the maximum and minimum values for 积分I at any time.
• 2. Clear when not running. When the system judges that it is not running, it will actively clear 积分I to zero.

PID of 微分D (suppressor)

I continue to look at the suppressor 微分D , it can also be understood as predicting the future, using the current 偏差量 minus 下一次偏差量 上一次偏差量 , the result may be-- 下一次偏差量 ，用下一次偏差量计算中，就执行量过大， 目标量的问题。 The specific formula can be abstracted as:

比例P = 偏差量 * 比例P系数
积分I = 上一次积分I + 偏差量 * 积分I系数
微分D = ( 偏差量 - 上一次偏差量 ) * 微分D系数
执行量 = 比例P + 积分I + 微分D

To change the example of "car brakes", when a vehicle is driving smoothly, when a red light is found in front of it, in order to make the driving smooth, basically release the accelerator and apply the brakes dozens of meters in advance. When the vehicle is very close to the stop line, the brake is applied hard to stop the vehicle. The whole process can be regarded as a control strategy of adding 微分D .

偏差量是越来越小的， 微分D = ( 偏差量 - 上一次偏差量 ) * 微分D系数 must be a negative number, add a negative number to the control, its function is to prevent the car from crossing the stop line due to untimely braking.

It is understood from common sense that the closer you are to the stop line, the more you should step on the brakes deeply and not let the car cross the line, so the role of this 微分D can be understood as braking. When the car is very close to the stop line and the speed is still very fast, the absolute value of this 微分D (actually a negative number) will be very large, indicating that the brakes should be applied to stop the car as soon as possible.

Going back to the above example of "adding water to the tank", when it is found that the water in the tank is approaching 目标量 , adding 微分D can reduce the extent of excessive water addition, which means reducing the control vibration in the process.假设目标量是1，每次漏水0.1， 比例P系数 0.5， 积分I系数 0.2， 微分D系数 0.2，我们再从头模拟Add water test, the specific values are as follows.

The last round of experiments used the joint control of 比例P and 积分I , and the highest water level reached 1.3. After exceeding 目标量 , the lowest water level dropped to 0.83. After adding the suppressor 微分D in this round of experiments, the highest water level only reached 1.23. After exceeding 目标量 , the water level dropped to a minimum of 0.88. Compared with the previous round of experiments, the oscillation amplitude of this round was obvious. decrease, this is the inhibitory effect of 微分D .

分享一个动图，很好的展示比例P 、 积分I 、 微分D的控制效果，其中红色虚线是目标量 ，曲线It is the change trend of 当前值 . Combined with this animation, let's recall the example of "adding water to the tank", is the control effect very similar~

PID principle summary

We used the example of "adding water to a water tank" to explain in detail the PID's 比例P , 积分I , 微分D the control principle of the three parameters Already understand what is PID. When you look back at this formula, don't you think it's kind of friendly.
$u(t)=K_p * e(t) + K_i * \sum_{n=0}^te(t) + K_d * (e(t) - e(t-1))$

• $K_p$ —— the proportional coefficient of the controller;
• $K_i$ —— the integral coefficient of the controller;
• $K_d$ —— the differential coefficient of the controller;
• $u(t)$ —— output signal of PID controller;
• $e(t)$ —— the difference between the given value $r(t)$ and the measured value (deviation);
• $e(t-1)$ —— The difference between the last given value $r(t)$ and the measured value.

Finally, to sum up:

• 比例P , 积分I , 微分D are related to 偏差量
• 比例P depending on current 偏差量
• 积分I accumulate the sum of all past 偏差量
• 微分D Predict the next moment 偏差量

Therefore, it is often said that 比例P is the present, 积分I is the past, 微分D is the future, is there a philosophical feeling, haha~

PID parameter tuning formula

Finally, I share a PID parameter tuning formula, which is well written and rhymes~

Parameter tuning to find the best, in order from small to large;
First, proportional, then integrate, and finally add the derivative;
The curve oscillates frequently, and the proportional dial should be enlarged;
The curve floats around the big bay, and the scale dial turns to the small;
The curve deviates and the recovery is slow, and the integration time decreases;
The curve fluctuation period is long, and the integration time is longer;
The oscillation frequency of the curve is fast, first reduce the differential;
Momentum is large and fluctuations are slow. Differentiation time should be extended;
The ideal curve has two waves, with the front high and the back low 4 to 1;
One look at the second adjustment and more analysis, the adjustment quality will not be low;
To increase the response, increase P and decrease I;
To slow down the response, decrease P and increase I;
If the ratio is too large, it will cause system oscillation;
If the integral is too large, it will cause the system to become sluggish.

reference

• Baidu Encyclopedia-PID Algorithm
• Baidu Encyclopedia - Open Loop Control
• PID control entry principle: https://zhuanlan.zhihu.com/p/197927959
• PID control algorithm principle: https://zhuanlan.zhihu.com/p/39573490
• PID control principle and control block diagram description: https://www.dgzj.com/zidonghua/96044.html
• PID parameter adjustment, personal experience: https://blog.csdn.net/weixin_44407238/article/details/119255699
• Learn PID-Based Cricket Balance System: https://www.bilibili.com/video/BV1xL4y147ea

If you have any questions or suggestions, please go to the public account [Jie Geshe] to leave a message~