BigDecimal detailed explanation and precision problems

BigDecimal is a knowledge point that is often asked in Java interviews in Dachang.

"Alibaba Java Development Manual" mentioned: "In order to avoid loss of precision, you can use BigDecimal to perform floating point operations".

Is there a risk of losing precision in the operation of floating-point numbers? Indeed it will!

Sample code:

 float a = 2.0f - 1.9f;
float b = 1.8f - 1.7f;
System.out.println(a);// 0.100000024
System.out.println(b);// 0.099999905
System.out.println(a == b);// false

Why do floating-point numbers float or double risk losing precision?

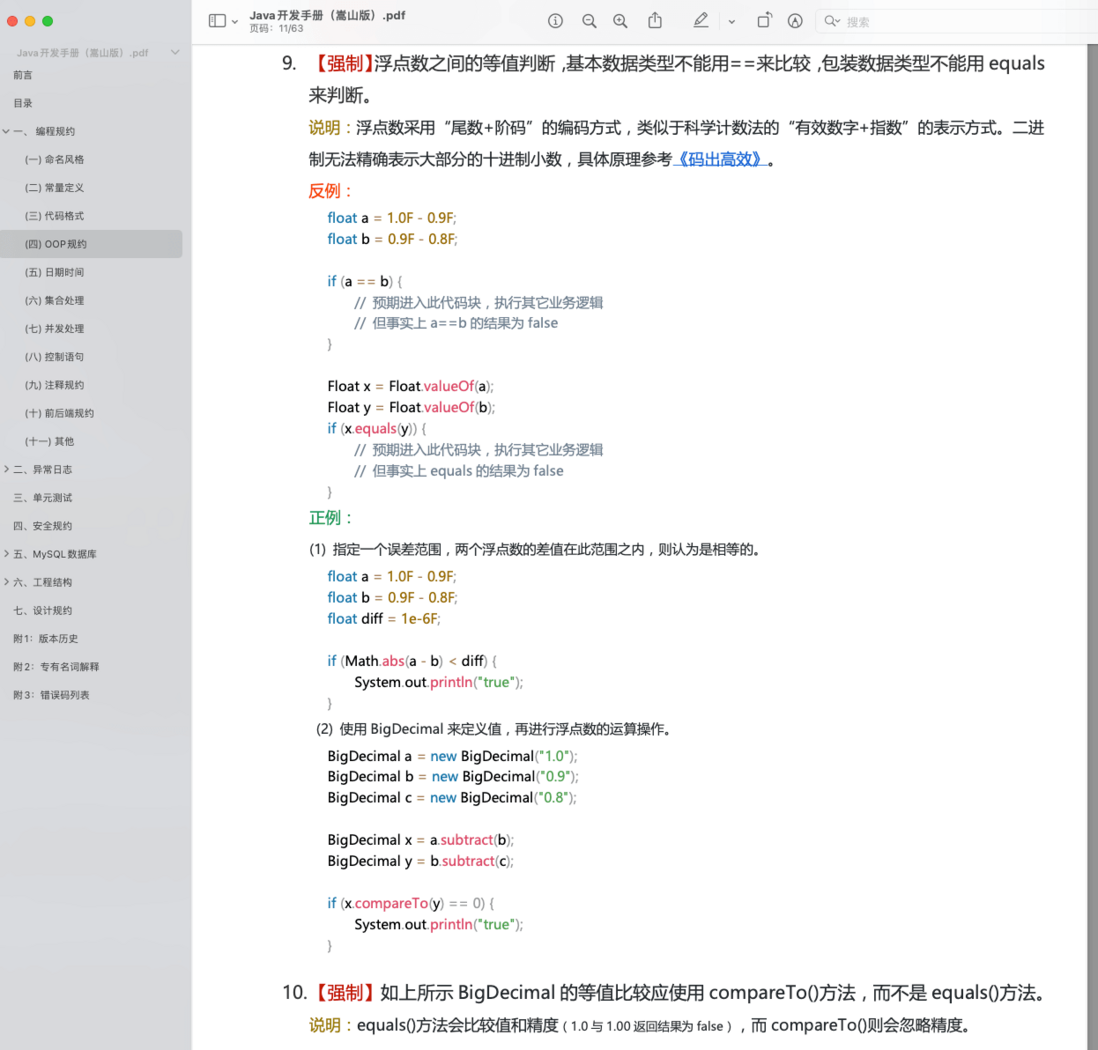
This has a lot to do with how the computer stores floating point numbers. We know that the computer is binary, and when the computer represents a number, the width is limited. When the infinite loop decimal is stored in the computer, it can only be truncated, so it will lead to the loss of decimal precision. This also explains why floating point numbers cannot be represented exactly in binary.

For example, 0.2 in decimal cannot be accurately converted to binary decimal:

 // 0.2 转换为二进制数的过程为，不断乘以 2，直到不存在小数为止，
// 在这个计算过程中，得到的整数部分从上到下排列就是二进制的结果。
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0（发生循环）
...

For more information on floating-point numbers, it is recommended to read the article on computer system fundamentals (4) floating-point numbers .

Introduction to BigDecimal

BigDecimal can perform operations on floating-point numbers without loss of precision.

Under normal circumstances, most business scenarios that require accurate calculation results of floating-point numbers (such as scenarios involving money) are done through BigDecimal .

It is mentioned in "Alibaba Java Development Manual": For the equivalence judgment between floating-point numbers, basic data types cannot be compared by ==, and package data types cannot be judged by equals.

The specific reasons have been introduced in detail above, so I won't mention them here.

To solve the problem of losing the precision of floating-point operations, you can directly use BigDecimal to define the value of floating-point numbers, and then perform operations on floating-point numbers.

 BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
BigDecimal c = new BigDecimal("0.8");

BigDecimal x = a.subtract(b);
BigDecimal y = b.subtract(c);

System.out.println(x.compareTo(y));// 0

BigDecimal common methods

create

When we use BigDecimal , in order to prevent loss of precision, it is recommended to use its BigDecimal(String val) construction method or BigDecimal.valueOf(double val) static method to create objects.

This part of the content is also mentioned in the "Alibaba Java Development Manual", as shown in the following figure.

addition, subtraction, multiplication and division

The add method is used to add two BigDecimal objects, and the subtract method is used to subtract two BigDecimal objects. The multiply method is used to multiply two BigDecimal objects, and the divide method is used to divide two BigDecimal objects.

 BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.add(b));// 1.9
System.out.println(a.subtract(b));// 0.1
System.out.println(a.multiply(b));// 0.90
System.out.println(a.divide(b));// 无法除尽，抛出 ArithmeticException 异常
System.out.println(a.divide(b, 2, RoundingMode.HALF_UP));// 1.11

It should be noted here that when we use the divide method, try to use 3 parameter versions, and RoundingMode do not choose UNNECESSARY , otherwise it is likely to encounter ArithmeticException (when the infinite loop of decimals cannot be divided), where scale represents how many decimal places to retain, roundingMode represents the retention rule.

 public BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode) {
    return divide(divisor, scale, roundingMode.oldMode);
}

There are many retention rules, here are a few:

 public enum RoundingMode {
   // 2.5 -> 3 , 1.6 -> 2
   // -1.6 -> -2 , -2.5 -> -3
             UP(BigDecimal.ROUND_UP),
   // 2.5 -> 2 , 1.6 -> 1
   // -1.6 -> -1 , -2.5 -> -2
             DOWN(BigDecimal.ROUND_DOWN),
             // 2.5 -> 3 , 1.6 -> 2
   // -1.6 -> -1 , -2.5 -> -2
             CEILING(BigDecimal.ROUND_CEILING),
             // 2.5 -> 2 , 1.6 -> 1
   // -1.6 -> -2 , -2.5 -> -3
             FLOOR(BigDecimal.ROUND_FLOOR),
       // 2.5 -> 3 , 1.6 -> 2
   // -1.6 -> -2 , -2.5 -> -3
             HALF_UP(BigDecimal.ROUND_HALF_UP),
   //......
}

size comparison

a.compareTo(b) : 返回-1 表示a小于b ，0 表示a b ， 1 表示a is greater than b .

 BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.compareTo(b));// 1

keep a few decimal places

Use the setScale method to set the number of decimal places and the retention rules. There are quite a variety of retention rules, you don't need to remember them, IDEA will prompt them.

 BigDecimal m = new BigDecimal("1.255433");
BigDecimal n = m.setScale(3,RoundingMode.HALF_DOWN);
System.out.println(n);// 1.255

BigDecimal equivalence comparison problem

"Alibaba Java Development Manual" mentioned:

BigDecimal Use the equals() method to perform equivalence comparison with a problem code example:

 BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
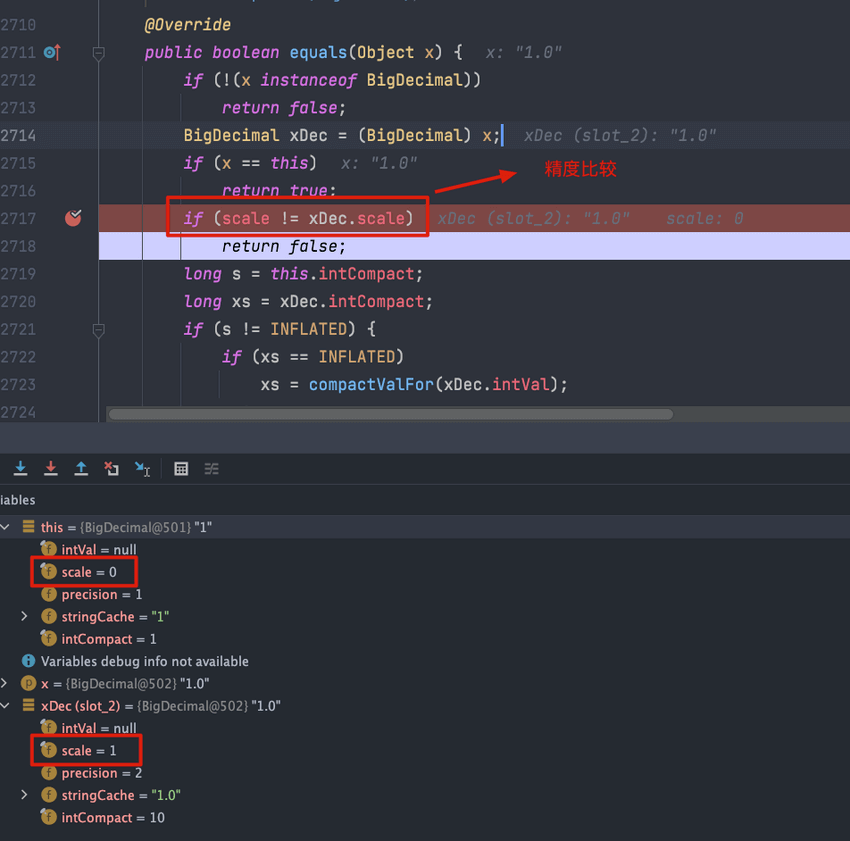
System.out.println(a.equals(b));//false

This is because the equals() method will not only compare the value but also the precision (scale), and the compareTo() method will ignore the precision when comparing.

The scale of 1.0 is 1, and the scale of 1 is 0, so the result of a.equals(b) is false.

compareTo() The method can compare the values of two BigDecimal , if they are equal, return 0, if the first number is greater than the second number, return 1, otherwise return -1.

 BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
System.out.println(a.compareTo(b));//0

Summarize

There is no way for floating point numbers to be represented exactly in binary, so there is a risk of loss of precision.

However, Java provides BigDecimal to operate on floating point numbers. The implementation of BigDecimal makes use of BigInteger (used to operate large integers), the difference is that BigDecimal adds the concept of decimal places.