旋转矩阵的一点思考

旋转矩阵

旋转坐标轴还是旋转坐标？有什么区别？相信很多人都有过类似的问题，这里我来简单尝试着理解一下。

旋转矩阵的相关知识请查看维基百科旋转矩阵

需要注意的是 Roll Pitch Yaw 的定义：

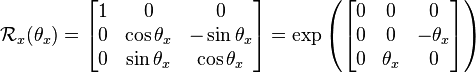
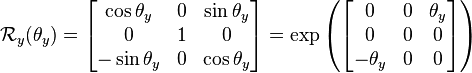
这里的旋转矩阵是需要左乘的，而且以逆时针为正。

关于左乘和右乘:
R是一个旋转矩阵，X是一个三维列向量[x,y,z]'。
RX就是把X旋转。
(RX)'=X'*R',看R'就是一个右乘的旋转矩阵，但是左边必须要是行向量。

坐标轴的旋转：

下面来说坐标轴的旋转：
以二维坐标系为例，命名为B1，如图：

为理解方便，我们再假设有一个固定的世界坐标系G，和该坐标系是重合的。
现在将坐标系B1其绕原点顺时针旋转90度，旋转矩阵R1是：

R1 = [0 1 0; 
     -1 0 0;
      0 0 1]

得到新的坐标系B2，如图：

原来坐标系B1上的点A，在G中的坐标，记为C1,是 (1,0,0)，旋转之后,A在G中的坐标是不变的，但是在B2中的坐标,记为C2,变成了(0,-1,0)。这一点其实挺好解释的，因为B2相对于B1(也就是G)顺时针旋转了90度，那就相当于A点相对于B1到B2的变化是逆时针旋转了90度。
逆时针90度的矩阵，记为R2,是：

R2 = [0 -1 0; 
      1  0 0;
      0  0 1]

将其左乘A在B1中的坐标，就得到A在B2中坐标了。

R2实际就是R1的逆矩阵，这点也不难理解，R2R1X,就相当于先把X顺时针90度，再逆时针90度，还是X，即 R2R1X=X，R1 = inv(R2)。

仿佛有点规律了，RB1 = B2, 然后 C2 = inv(R)C1。
确实是这样，那怎么得到？我们来推导一下：

R*B1 = B2 
这一步实际上做了一个基底的变换，基底变了，但是还有下面这个等式：
B1*C1 = B2*C2
也就是说在不同基底下，我们还有同样的值
于是可以求出 C2 = inv(B2)*B1*C1 = inv(B1)*inv(R)*B1*C1
等等，刚刚不是说C2 = inv(R)*C1的么？别急，B1实际上是一个单位矩阵，可以以同B1重合的G为参考系理解一下。于是：
C2 = inv(R)*C1 = R'*C1

旋转坐标系时旋转矩阵的列

• 第一列，将原来的X轴旋转到什么坐标(在原来的坐标系下)
• 第二列，将原来的Y轴旋转到什么坐标(在原来的坐标系下)
• 第三列，将原来的Z轴旋转到什么坐标(在原来的坐标系下)

比如R1*B1之后:

• B2的X轴是在B1坐标系的(0 -1 0), X轴是原来的-Y轴
• B2的Y轴是在B1坐标系的(1 0 0)，Y轴是原来的X轴
• B2的Z轴是在B1坐标系的(0 0 1)，Z轴不变