一起来复习Data Science：那些让人抓狂的回归分析

回归分析（regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。在此，我讲会从机器学习和统计学两个方面分别描述回归在两个领域中的区别。

线性回归

常见的线性回归基于以下模型：

$$Y = \beta X + \epsilon$$

简单最小二乘法回归

---

最小二乘法实际利用的是残差控制，即

$$argmin{RSS}$$

其中RSS为：

$$RSS = \sum{(y_{观测值} - y_{预测值})^2}$$

而在机器学习中RSS也被称作最小二乘法的代价函数（Cost Function）。

可以简单推导，参数解为

$$\hat{\beta} = (X^TX)^{-1}X^Ty$$

简单地测试指标

1. R方（也称Pearson相关系数）
   简单地说，即计算$$R ^ 2 = \frac{E((X - \overline{X})(Y - \overline{Y})}{\sigma_x\sigma_y}$$

2. F检验
   F检验是用来检验参数的显著性，H0假设为$$\hat{\beta} = 0$$

回归的扩展

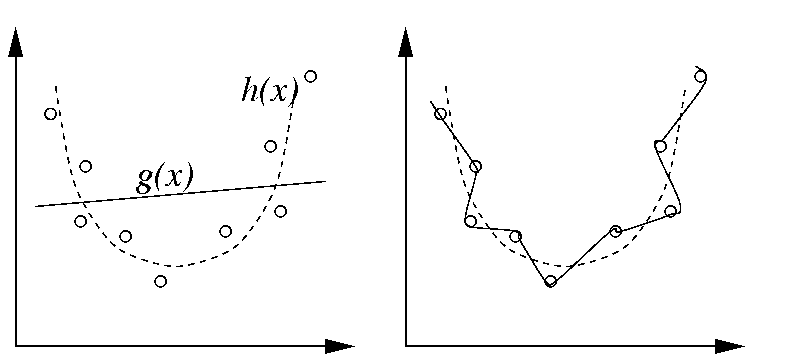
当一元回归无法满足要求的时候，也会对自变量的乘方进行处理，进行多项式回归。随着使用的乘方数目的增加，其R方总是越来越小。此时就会产生过拟合（overfitting）的问题，可以理解成以下状态：

而常用的控制过拟合的方法就是下面要提到的岭回归和Lasso回归。

岭（Ridge）回归和Lasso回归

---

概念引入

这两个概念更关注模型的拟合程度、bias、variance。

Bias和Variance

我们首先要量化模型的偏差和方差。

我们用f(x)表示实际模型，则显然RSS可以写作：

$$RSS = E((f(x) - \hat{f}(x)) ^ 2) = (E[\hat{f}(x)] - f(x))^2 + E[(\hat{f}(x) - E(\hat{f}(x)))^2] = Bias(f(x)) + Var(f(x))$$

显然，模型的平均准确程度好坏直接由Bias(f(x))来判断，而模型的是否容易受到样本的细微影响则直接由Var(f(x))来判断。而显然，过拟合所要解决的问题是使得Var(f(x))变小。

shrinkage regression

显然，当出现过拟合时，参数β的变异程度会大幅度增加，因此，我们只要在惩罚函数中加上这个变异程度的量化指标就行了。在最终结果中显示，就是拟合的函数波动明显缩小，因此这类用来缩小（shrinkage）波动的回归就叫“shrinkage regression”，常见的方法就是岭回归和Lasso回归。

岭回归和Lasso回归

其惩罚表达式分别为：

$$Cost_{ridge}(\beta) = RSS_0 + \lambda\sum{\beta^2}$$

$$Cost_{LASSO}(\beta) = RSS_0 + \lambda\sum{|\beta|}$$

而通过绘制λ和参数的图形，就可以来确定λ的大小。

此外，惩罚函数也可以从拉格朗日函数的方式理解，其实Lasso和岭回归都是控制

$$\sum{|\beta|^p} \le t$$

在数学分析/微积分教材中可知，约束条件下的拉格朗日函数形式就是上面表述的两个惩罚函数。

因此，另一个评估shrinkage的方式就是计算参数与最小二乘法获得的参数的绝对值比，即

$$s = t^{\lambda,shrinkage} / t ^{ls}$$

弹性网回归

弹性网回归其实就是结合Lasso和岭回归，并设置权重的回归，即控制系数t为

$$\sum(\alpha\beta^2 + (1 - \alpha)|\beta|) \le t$$

分位数回归（Quantile Regression）

分位数回归其实思想上讲是要控制OLS（普通最小二乘法）回归中的异常值处理不佳的问题产生的。

概念引入

在实际建模之中，OLS总是在有特殊值（Outlier）或者异常值（Anomalies）时表现不好，例如下图：

虽然只有一个特殊值，但是明显，右图显示的回归结果就差强人意了。用来衡量少量异常样本对于最后模型的影响，我们提出了鲁棒性（Robust，或稳健性）的概念。

中位数与均值

在刚接触统计学的时候，我们一定不会忘记教我们的三个描述性统计指标Median、Mean和Mode的区别，简单的图可以绘制如下：

我们可以看到，描述一个随机变量分布时往往Median和Mode的效果要好很多，但是为什么我们一直会选择均值作为描述性统计最常用的指标呢？原因概括主要有以下：

1. 在实际生活中，连续型随机变量的Median、Mode值很难估计。

2. Median的计算涉及排序，Mode的计算涉及计数，在计算机计算能力或者手中条件不允许的前提下，均值相对来说比较方便计算。

然而上面的例子已经看出有异常值的前提下，Median相对与Mean来说对分布的描述更为准确；而具有特殊值时，也是可以看出Median的优势的：

中位数回归

运用到回归之中，我们可以发现，也许计算

$$\sum|y_{观测} - y_{Median}|$$

的效果更好，因此，把上式作为回归的惩罚函数的回归也叫“中位数回归”。我们把这类更具有鲁棒性的回归也叫作“鲁棒性回归”或“稳健回归”（Robust Regression）。

进一步推广

中位数其实是τ = 0.5时的分位数，因此，我们可以推广得到一个分位数回归，即其惩罚函数为：

$$(1 - \tau)\sum_{q > y}(q - y) + \tau\sum_{q<y}(y - q)]$$

分位数回归的应用

其实在τ0分位数下的回归方程，描述的是x分布在F(X) = τ0时的回归样式，它会提供给我们比OLS更多的基于x分布的预测。