Algorithms, Princeton, Coursera课程整理与回顾

Princeton的算法课是目前为止我上过的最酣畅淋漓的一门课，得师如此夫复何求，在自己的记忆彻底模糊前，愿对这其中一些印象深刻的点做一次完整的整理和回顾，以表敬意。

注：
这是一篇更关注个人努力与完成任务项目过程相关的文章，内容集中于课程背后值得提到的部分，不会介绍课程基本信息及学习时必读的设定要求等部分，敬请谅解。
在学习一门课程的时候考虑为什么这么教是个人习惯，我会尝试给出一些解读，为什么这门课这么屌(awesome)。
优化无止境，越学习才能越深刻地感受自己的无知，即使是作业内已提到的额外内容我也并没有一一探究完整，这里只是谦卑地尽力记录自己的努力，并无意与谁比较，如有新的进展还会回来更新。
除特别标注外，文章非原创插图全部来自课程相关资源。
每一小节的作业题目链接到specification，“√”链接到checklist，“〇”链接到code下载。
这里提供一个全文完整的资源树。
剧透预警：
内容包含大作业的关键问题解法分析。

算法，第一部分

I. Union Find与Percolation √ 〇

作为第一部分开学第一课，作业Percolation可谓精妙：

1. 既没有复杂的语法使用（仅数组操作），又着实比在基础语言层面上升了一个档次；
2. 漂亮的visualizer动画效果激励着初学者完成任务；
3. 强大的autograder功能初次展现，评价算法的主要管道一目了然，每一微秒每一字节都很重要；
4. 针对学习迅速的同学还隐含了一个很大的挑战：在仅使用一个WeightedQuickUnionUF对象的前提下，解决backwash问题。

下面主要聊聊backwash：

问题的核心源自virtual top/bottom，一个强行被导师在课程视频中提到的优化方法，于是天真的同学们（我）就去开心地实现这个看似无辜而又性能楚楚动人的方法，却毫不了解导师在下一节中马上提出的backwash问题是何物，还觉得这种低级错误怎么可能会发生：

java-algs4 PercolationVisualizer percolation/input10.txt

……

（我发誓这就是我看到的东西……）
把痛碎的心小心拼回，认真思索一番后确定问题根源出在virtual bottom，一个显而易见的解决方案便浮现在眼前：使用两个UF，一个使用vb一个不用，判断percolate用前者，判断full用后者，解决！

Raw Score 100.00 / 100.00

然而checklist的一句话又引起了我的注意：

However, many students consider this to be the most challenging and creative part of the assignment (especially if you limit yourself to one union-find object).

加上autograder特别温馨的提醒“bonus failed”，我不得不重新开始审视这个问题。
后来的事实证明，直到课程结束没有一个问题再让我如此头疼。经过了一段可谓长征式的思考，加之在forum的讨论中得到了一点灵感(多加利用Find())，最终形成并实现了解决方案，方案核心如下（corner case另行处理）：

1. 将原方案中表示open状态的boolean数组改为byte数组，设定规则如下：初始化的默认值0代表blocked site，赋1代表open site，赋2代表与尾行相连的open site；
2. 每open一个site，如果位于尾行则赋2，否则赋1；
3. 分别对每个邻接site检测：如任何一方的root site对应byte值为2，将双方Union后的root site设为2。（root为Find()的返回值）

此方案下，判断open只需要对应byte>0，判断full使用UF结果准确，判断percolates检测virtual top的root site对应byte是否为2。

Raw Score 101.25 / 100.00
Test 2 (bonus): Check that total memory <= 11 N^2 + 128 N + 1024 bytes
==> passed

对这个作业来说，上面这三行的成绩凝聚了太多。

II. Resizing Array & Linked Lists与Randomized Queues and Deques √ 〇

第二周课程正式展开，但在作业深度上相对稍有下降，根据指定的性能和API要求，选择适当的实现方式（动态数组、单、双向链表），实现Randomized Queue和Deque，主要训练基本的算法分析和编程严谨性（完善处理corner-case），但并无特别的难点。有两个小技巧可以提出：链表可使用sentinel node(s)使代码更简洁（checklist已提），写client时可先shuffle再插入(bonus)。

2018更新：最近同学在做这道题时发现autograder已明确指出不可以使用数组，这就使得这个bonus变得有趣多了：
仔细想一下，既然API已经把我们非常严格地限制在只能遍历一遍输入的情况下，而我们仍然希望RQ不超过k个元素，那么在正常读入k个元素后面对下一个元素我们只有两个选择，dequeue一个旧元素然后enqueue新元素，或直接忽略这个新元素；所以问题的关键就变成了一个概率问题，两个选择应当如何权衡，才能保证每个元素最终留在RQ中的概率相等呢？
相对应地，autograder也有完整的假设检验(t-test)来实际检测，小伙子你真的做对了吗？
不必多说，撸起袖子上吧，捡起高中的排列组合知识，仔细分析一下，你算出的忽略当前新元素的概率应该是这样：
$$\mathrm{P}_{discard}=\frac{\mathrm{C}_{n-1}^k}{\mathrm{C}_n^k}=\frac{n-k}{n}$$
plug it in and feel the magic! 不得不说这个作业的设计之精巧，看似非常不起眼的一个小bonus，竟然也几乎是蕴含着Monte Carlo方法的一些基础启发，真是妙啊。

过程中一并学习了Java的Generics，Iterable，Iterator概念，在大学课程部分已学习掌握得比较熟练，可不谈，the result speaks：

Raw Score 100.19 / 100.00
Test 3 (bonus): Check that maximum size of any or Deque or RandomizedQueue object created is <= k
==> passed

结合两次作业特性，可看出一些值得一提的点：

• 作业任务要求与说明往往面面俱到细致入微，在给定公有API框架及其对应时间空间复杂度的基础上，结合课程视频知识内容，这种“受指导”的编程过程变得十分清晰，尤其是其中API的设计，风格简洁高效到自成一家，我认可自己的代码风格已很简洁，而algs4.jar让我第一次看到了更高；
• 给定充足的测试材料，包括各类corner-case或相对有趣的输入数据（如sedgewick60.txt），及合适情况下生动的可视化工具（如PercolationVisualizer.java），都使得学生可以全力，高效，有动力地，将精力集中在核心算法本身上。

III. Sorting与Pattern Recognition - Collinear Points √ 〇

本周的课程介绍了两大经典排序：Mergesort和Quicksort，自然作业也与sorting紧密相关。Collinear Points（找出所有4个或以上共线的点构成的点集）是第一个在运行时见证“好的算法”与“暴力算法”直观差别的作业，这样的对比能给学生带来深刻的影响：忙了好久，为了什么？

上图为暴力算法(~N^4)求解100个数据点(input100.txt)，下图为基于排序的算法(~N^2logN)求解1423个数据点(rs1423.txt)
测试数据还有很多。图中示例对快速算法给定数据量庞大了不止10倍，运行时间却与不到1/10数据量下的暴力算法接近；对上图数据，快速算法基本看不到找线的动画过程就完成了；对下图数据，暴力算法在可以忍受的时间里基本找不到几条线。
这样的运行结果可以给学生一种非常好的对自己努力的掌控感，正是这样一个个美妙的瞬间使学生能以最好的状态与饱满的好奇心在算法之路上继续走下去。
作业说明中对核心算法的描述非常清晰，应当特别小心的技术点（浮点误差、正负零等等）也都在checklist中予以强调，因而实现难度不算很大，其中使用了Java的Comparable与Comparator，排序过程调用Arrays.sort()，详细思考问题理清关系后，实现非常自然，前提是编程基本功必须扎实。
值得提到的点：

• checklist鼓励初学者开始编写快速算法时先不要担心5个或以上的点共线的情况，而实际上对基本功扎实的同学，从开始便考虑这个问题更为合适；
• checklist提到compare()和FastCollinearPoints类可以完全避免浮点数用整形运算实现，我想到的唯一符合要求（Point.java注释中规定不得依赖toString()）的方法是，对Point类的compareTo()方法返回值增加意义（不单纯返回正负1），以获取两点的坐标之差（因题目给定坐标取值范围0-32767，可在返回值低两位字节存储x坐标差， 高两位字节存储y坐标差），再利用坐标差判断斜率是否相等。虽依然完全符合题目要求，但已有一点奇技淫巧之嫌，并且不一定能够通过autograder（评分时会替换Point类去测试FastCollinearPoints），不多讨论。（更新：此方法已确定违反FastCollinearPoints的API。）

最终实现版本拿到了100分，未发现关于bonus的讨论。

IV. Priority Queue与8 Puzzle √ 〇

刚刚讲解完使用Binary Heap实现的Priority Queue，便迎来了这周的8 Puzzle——使用PQ实现A*解决NP难问题，所以——重点在优化咯。
(Image Source Here)
左边是目标状态，右边是起始状态；对，就是那个——小时候功能手机上的蒙娜丽莎。
随着学习的深入，这次作业的复杂度有了一个明显的上升，但这门课最美妙的地方之一也就在这里：面临的问题越来越复杂，而导师给出的指导思路依然保持最大程度的简洁优雅，每一步骤的设定都直指问题核心，并在实现功能基础上提供非常丰富的优化选择，以及每个优化会带来的影响分析。

"It's a funny feeling being took under the wings of a dragon. It's warmer than you think." —— Gangs of New York

整个问题相对比较复杂，但经过给定API的划分和给定的限制后，问题变成了实现一个个目标明确的小方法而已，其中最复杂的不过是A*的实现，而周到合理的封装和PQ的使用也使得这个过程无比自然，在此之前我从未意识到我可以将A*在如此短小清晰的代码中实现：（源码如此，仅省略了声明过程）

while (!pq.min().board.isGoal()) { 
    cur = pq.delMin();
    for (Board nb : cur.board.neighbors()) {
        if (cur.prev != null && nb.equals(cur.prev.board)) continue;
        pq.insert(new Node(nb, cur.moves+1, cur));
    }
}

PQ使用了Manhattan Priority作为Comparator，Node为封装Board的单链表节点，结束后获取最短路径只需取PQ中最小Node，利用prev指针遍历。
解决8 Puzzle这一NP难问题的核心代码便完成了。
当然，在其余部分还是有不少值得提到的点：

• 用char[]存储一个Board的状态比用int[][]好太多，但使用前需要详细测试将char做数字使用与直接用int的区别；
• Board的equals()方法只需比较char[]构成的String即可，早期因图省事直接比较了toString()的返回值（one-liner），造成了很大的性能损失，最后寻找问题来源也费了不少功夫（教训：看似再简单的部分也要在脑袋里多转一转再下手，devil in the details，…，you name it）；
• Solvability: 这篇文章描述的解决方案应为checklist所述方案，但需要脆弱地依赖toString()反推Board内容，在本期课程的API设定中已被明确禁止，要求使用两个同步A*的方案解决（最好使用一个PQ），但未来session可能会在两方案对应API设定间切换，所以我都实现了一遍，上面出现的A*代码来自文章所述方案；
• 实现Priority的cache时需要稍多做思考，直觉想到的第一方案是储存在Node中与A*过程配合，而这将使A*代码迅速肿胀，且没有很好地利用更多规律：如checklist所指出，对相邻Board每次重新计算Priority其实也有很多重复工作，我的做法是将cache过程作为Board类一个私有构造函数，构造相邻Priority只需做对应增量操作即可，以最简洁的手段达到了目的。

我的最终测试文件及结果在这里，运行于i5-2450 (8G)，结尾几个复杂的4x4开始因内存不足报错，论坛查到大概需要5-6G超出了我的空闲内存，即使要测也会用到虚拟内存，因而结果参考意义不大。
对于这个作业，努力的最终汇报便是，看着终端中puzzle一个个被正确解决沾沾自喜，然后到相关的拓展材料中去体验无知，发现更大的世界。

V. Search Trees与Kd-Trees √ 〇

这一周的Balanced Search Trees课程令我印象深刻。在进入作业讨论前，我希望先聊聊这次的课程内容：
在前一周的课程中就已引入了二叉树的概念，一个无比经典的数据结构，这我在大学课程中便已了解到，只是认识非常浅薄，并从未，也从未认为我能够，动手实现过。
可如果说在上一周的学习中弥补了我的这个问题，对二叉树有了更深刻的理解，那么这一周的课程彻底颠覆了曾经心中幼稚的见解，所谓质变，我应该是在这里体会到的：

• 从小学四年级开始在少年宫学习BASIC到初中的PASCAL，以致虽然后来停止学习，但因为接触时间远早于同龄人而在此方面经历了各种优势，但从小在我心中“程序”，以及它背后所代表的机械逻辑始终被认为是“就那么回事儿”的。我天真地认为自己早已掌握“程序”界的终极真理，无非就是严丝合缝一步不差地执行、再执行，只要“机械”性地认真下去，便没有什么解决不了的，以至于从小就在性格中造就了一面“彻头彻尾的唯物+实用主义者”，不相信任何世间美好。
• 有这句天真的话在前，接着慢慢成长，读书，行路，阅人，历事，自然会学到原来这个世界真的不是那样，开始理解爱与人性，开始理解这个世界的美妙。加上比较幸运，因而“唯心+浪漫主义者”的一面在我的性格里也发展得很好。但大学开始继续学习计算机，多少，对“程序”这一彻头彻尾“唯物+实用”精神的产物，还是抱着一些看法的。

结束这一周的课程学习后，我改变了这个看法。
课程开始先讲解了2-3 search trees，一种引入了新规则树型结构。这是一个“理解容易，实现复杂”的Symbol table方案，它可以对任何输入数据保证树形结构的平衡以达到保证各项操作logN的复杂度，而规则却足够简单到可以在课堂中很快描述清楚，可以算是课程中第一个令我惊艳的算法。
这时我想：果然在一步步深入后算法变得高深莫测了起来呢，这个2-3 tree，理解起来容易，要实现起来可真是困难呐。已经不是二叉树那么简单的东西了，以后是不是只会更难啊，看来我遇到了一个屏障，这是不是我能走到的最远了啊。（开始有一点点担心）
直到视频结尾出现关于implementation的讨论：

Bottom Line: Could do it, but there's a better way.

紧接着下一节就是我们的主角：左倾红黑二叉树(LLRB)。
它只做到了一件事：将2-3 tree带回了二叉树世界，却仅对朴素的二叉树做极其微小的改动——每个节点增加1 bit，用以表示“颜色”，加之无比简洁的引导，便在现实世界中实现了原先只是构想的2-3 tree几乎全部的优点。
红黑树本身就是70年代Sedgewick教授参与提出的，而LLRB是由他一手提出的极其简洁的红黑树实现版本，尤其是它的insertion，在课堂上作为重点讲解，仅在原朴素二叉树实现代码基础上，增加了3个小工具函数（左旋、右旋、翻转）和递归插入过程中的4行代码（如图），便完成了所有工作。

在彻底理解LLRB后，我想我被征服了。程序不再仅仅是彻头彻尾“唯物+实用”精神的产物，而是我们理解世界的工具，也见证着我们改变世界过程，它与其他一切事物一样，可以充满真正的美。
我想可以这样评价红黑树背后的思想：

• 它就像人类从蒙昧时代开启智慧的一道光，将原来松散无序的组织变得优雅而高效，并且还尊重了所有旧时代的传统；
• 也正是因为尊重传统，才使得新的秩序得以稳定存在；
• 新的秩序完整了传统，成为了传统当中，最为亮丽的部分。

这样的成果也不是凭空出现的：

• 勇于跳出传统的框框，用自由的视角审度；（2-3 tree已不是二叉树）
• 回到现实在一点一滴中细腻体验；（发现除繁琐的直接实现外其他实现方式的可能性）
• 不妄自菲薄出身，用尊重的态度行动。（选择回到经典二叉树模式，试图在旧传统上建立新秩序）

知行合一，至此可谓正途。

同为插入255个随机节点，左图为朴素二叉树，右图为左倾红黑二叉树。

作为第一部分的最后一个作业，kd-tree其实难度没有它看起来那么大。课程部分已很完整地讨论过很多种经典的树形结构（分析+实现），到这个阶段学生应已对树形结构非常熟悉了，实现kd-tree已是水到渠成。

同样的，编程严谨性在这个作业中变得更加重要——情况相比前几周又要复杂一些，从零编写一个特定（且不简单的）规则下运行的树形结构，主要功能是高效地插入与查找；
这次的作业同样包含了一个暴力算法的版本（使用默认的红黑树结构），除了在执行效率上可以做比较外，还提供了一个重要的软件工程思路：面临一个较为复杂，而优化空间很大的问题时，先实现一个最简单的暴力算法版本检测结果（往往可以非常简便地实现），再考虑进阶的算法与数据结构实现性能优化，并在实现期间，暴力算法可以作为检验算法正确性最直接的参考。
实现过程中值得提到的点：

• 节点的奇偶性是一个不小的麻烦，编写需要十分谨慎，我的做法是在Node类中添加了一个boolean用以表示奇偶，相信一定有更好的方法（不存储RectHV），还会回来探索；
• Nearest Neighbor的查找过程需要思考清楚，剪枝的界限十分清晰，尤其是剪裁其中一个子树的条件：如果本子树中找到的最近点与给定点距离 已小于 给定点到另一子树矩形区域的距离（点到点距离比点到矩形距离还近时），才能跳过另一子树的遍历过程。

左图为Nearest Neighbor，右图为Range Search。（根据鼠标状态信息）
图中红色部分为暴力算法运行结果，蓝色部分为kdtree运行结果；在增加数据量后单独测试，暴力解法效率明显下降。

算法，第二部分

在一个学期的辛苦努力后，带着满满的收获与日益成熟的头脑，第二部分正式开始了。

“相信经过了第一部分的学习同学们都会有很大的提高，短暂休息后也恢复了饱满的学习热情，那么我有理由相信你们准备好了接受点真正的考验。”
—— 视频中永远不会提到的导师内心独白（历经折磨后的脑补）

第二部分在课程与作业两个方向的难度都比第一部分提升了一个档次。好在不巧被导师言中，我的确有非常好的提升感和新一轮的热情。
所以，放马过来吧。

VI. Directed Graphs与WordNet √ 〇

第一周便直奔主题，开启了数据结构领域的又一大领域：图。
课程中出现了一个很有趣的分类值得提到，是形容问题难度的：

1. 任何程序员都能够解决。
2. 典型的勤奋的算法课学生能够解决。
3. 雇佣一个领域专家。
4. 非常难。
5. 没有人知道难度。
6. 已证明不可能解决。

并举出了一些符合条件例子来说明这些分类，当然可以料到的，有很多难度2的例子。
这针鸡血打得，啧啧啧，不留痕迹。
很好。诸位红着眼的同学，准备变身吧。

第一周的作业是WordNet，少了第一部分作业多图多动画的喧闹，不再为搏人眼球而吵吵嚷嚷，却在安静的terminal和脑中的抽象之海中展开了一场货真价实的战斗。
因文字方面中西文化背景截然不同，导致WordNet的概念不太方便简单地描述清楚，但作业说明中已解释得比较详细，这里只放一张示意图：

整个作业可以分为三大部分：选择合适的结构存储结构复杂的词典及其网络关系（基本功），实现正确高效的广度优先遍历计算SAP（难点），和在此基础上一层一层更细致的优化（进阶）；
本次也是checklist优化部分唯一标注optional的作业，因为的确实现起来有难度；分布如上所注。
词典(synsets)为ID与单词的多对多关系（一词多号，一号多词，释义仅供参考无需读取），上下位关系(hypernyms)是以ID为单位的树形结构（图中的箭头关系），可以明显看出hypernyms使用有向图表示，synsets存储方式取决于访问需求，因程序中正反都会使用（以词求号，以号求词，求词存在），我选择了空间换时间：

    private ArrayList<LinkedList<String>> synset; // 以号求词（获取SAP中的ancestor对应的单词）
    private HashMap<String, LinkedList<Integer>> ids; // 以词求号（获取索引单词的ID以计算SAP）
    private HashSet<String> nouns; // 求词存在（API需求功能）
    private SAP sap; // 有向图

文件读取过程稍繁琐，编程习惯要良好，保持谨慎不会错。
接着是SAP的实现，这里周旋的余地很大，一定要认真思考问题本质，并多考虑一些特殊情况检测自己的想法，再开始下手去做，并如checklist所强调，不要轻易尝试直接实现优化版本，因为细节繁琐不易考虑周全，而可能带来的潜在问题非常多，每实现一部分都要做周全的测试确保无误才行。（尽管最终成功的优化，也可能仅仅是几行的改变而已）
这里要提到的点（细节）：

• 在checklist提到的三个优化选择中，我选择了相对保守，但工作良好的优化方式：每次的搜索初始化使用HashMap构造函数；正确实现了两端同步运行的BFS，并提供了提前结束的出口；只缓存了单个ID（单个节点与单个节点）的查询结果；
• 对单ID缓存的存储方式，我的symbol table使用了一种很直接的无重合又简单的hash计策：给定查询ID为v与w，总ID数为V，则查询结果的编号记为：

(V-1)+(V-2)+(V-3)+...+v+(w-v)，化简后为(V-1)v-(vv+v)/2+w。

• 提前结束BFS的出口开始时没有考虑清楚，就暂时没有添加，提交的版本拿到了103.12；后来仔细思考，发现了这部分余地，仅增加了一行代码，分数便提高了不少；
• SAP同时支持DAG与DCG（有环图），仔细分析如下这个特殊情况可能有助思考：（给定节点1与8，求其SAP）

(Made with Graphviz)

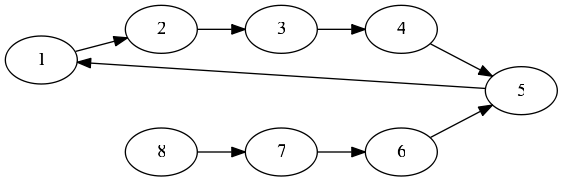
• BFS如由节点1先开始，则轮到第4次迭代时，节点1遍历，发现共同祖先节点5，路径距离为4+3=7，但此时不能停止搜索；实际SAP的共同祖先为1，路径距离为0+4=4，是在第4次迭代的节点8遍历部分被发现的。

在这门课程的通用说明中便已提示过，不要把autograder当作debug的工具，以省去自己发现问题的过程；我必须保持诚实：至少，对于我这样编程时基本“实用”精神至上的性格来讲，因为autograder在各个方面都真的很完善，很多时候这是一条很难遵守的规定，所以我也体会到了这样做的坏处：对于温室中的作业来说有便利的autograder帮助简直美好，但real world problem永远是残酷的；在这个作业中，我想我失去了一些很宝贵的机会，利用充足的测试材料亲自去到那些数据的最深处游荡，去体会探索算法的优劣，这个过程简直是最迷人的部分（如上示例）；意识到这些后，有一种作弊的愧疚感；每个人都应当正视它们，然后作出自己的选择。
最终成绩为106.25，具体Bonus点可以看这个文件。
守得云开见月明。

VII. Shortest Paths与Seam Carving √ 〇

本周作业算是一个“轻松有趣”的短暂休息；轻松到checklist都不知道该写点什么好了……
在第一部分结束后休息的阶段，因为十分惦记完成这门课作业的快感，于是到booksite转悠了好久，又完成了一些额外的项目；
（完整项目下载：N-Body，Barnes-Hut (很美)，Atomic Nature of Matter）
而紧接着在booksite推荐的Nifty Assignment中便见到了这个作业，感觉很是惊艳，但还没有动手做，没想到这么快就又见到它了。

（取自源SIGGRAPH2007介绍视频，2008推出改进版）
作业中值得提到的点其实不多，大部分功能的实现都非常直接，中间加入了一点图像处理的入门知识，同样也非常好理解，重点是最短路径的BFS：

• 对于固定值边界的处理比较繁琐，需要仔细处理；
• 对很多图像处理问题，虽处理对象大体上还符合“图”的定义，但因为很多图像固有的因素，会将问题简化得多，不必再使用重量级的Digraph类，就事论事地解决问题即可；
• 要找到能量最小的seam需要对整个图像计算路径距离，我的做法是维护distTo（最近距离）和edgeTo（最近距离对应“父节点”）两个数组，遍历全图后在最后一行（列）找到distTo的最小值即为所求seam的尾元素，通过追踪edgeTo即可得到所求seam。
• energy的复用是一个小难点，需要认真考虑每移除一列或一行seam后，哪些情况下的点应该被重新计算，参考作业说明的vertical-seam.png、horizontal-seam.png或下图去分析，可能会有帮助：

• 我想到的转置的目的是为了在纵横两个方向都能利用System.arraycopy()的高效，开始时我没有做这项优化，是手写了removeHorizontalSeam()的这个过程，因已达到了满分要求便没有再优化。

VIII. MaxFlow与Baseball Elimination √ 〇

MaxFlow将是本课程接触的最复杂的图论问题了。别这样，我才刚刚兴奋起来……
同样地，作业Baseball Elimination是一个非常巧妙的Maxflow应用，甚至都与“流量”没有任何关系：
根据实时赛季数据，通过建立流量模型，判断当前局势是否已出现被“数学上淘汰”的队伍（已无法再获得冠军）；

虽然算法上十分有趣，但个人并不喜欢这道题背后某个方向的思维：对辛苦奋战的运动员来说，每场比赛都是战斗，每个细节的表现才定义了自己，不是由一群snobbish的“科学家”说你被“数学上淘汰”了，你就真的毫无希望了；
当然同时要明白这只是“黑暗版”的理解，对于专业选手来讲任何信息都有其价值，在赛前以最清楚的数据明确自己的处境，以更好地调整战略、激励人心，再参与比赛，才算是真正在现实世界用出了好算法的最大价值。
Again, all in all，要nerdy地热爱，但不要做nerd。
同如修行的和尚，功德要回向众生，而禅喜，留给自己就好。

本次作业在细节上有一些非常简单的小技巧可以帮助简化实现（简洁性也是checklist提示的，参考代码不到200行，我的版本为150行左右），但可能不是第一次思考时就能想到：

• 在读取文件数据时就可额外计算（保存）一些后期需要的数据：目前榜首队伍与获胜场数（用于简单淘汰），和以双方队伍为单位的比赛场次（用于建立FlowNetwork的顶点数）；
• "Do not worry about over-optimizing your program because the data sets that arise in real applications are tiny." 对我的思路，这意味着无需考虑FlowNetwork的复用问题——一个早期造成很多痛苦的优化尝试；
• FordFulkerson类的使用实际上使问题仅剩下了建模部分，且在说明中已解释得非常详细，故实现十分直接。

IX. Tries与Boggle √ 〇

然而Boggle却是第二部分课程作业中，最有挑战性的一个。（因为我没有拿到Bonus T_T）

“The goal on this assignment is raw speed—for example, it's fine to use 10× more memory if the program is 10× faster. ”

（“明确地”暗示使用Trie）
从动手开始做本次作业，到基本感到没有优化余地，我的代码经历了大概4-5个大版本的改变，小的修正与优化更是不计其数，即使是这样一个固定情形下的问题，也令我好好体会了一次，程序迭代更新、不断修正与优化的过程。

本次任务相当于编写图示游戏的AI部分——BoggleSolver，而要拿到满分以至Bonus，需要一秒内解决成千上万个Boggle Board。
下面是我经历的迭代过程的简短介绍：（只选出了几个典型版本，括号内为autograder针对getAllValidWords()的时间测试，值为5秒内调用次数的reference / student ratio，越小越快；满分要求小于2，Bonus要求小于0.5；源材料没有保留完整，数据可能稍有出入）

• 一版（~2.5）：简单更改库中现成的TST（三叉搜索树）类（增加一个单行的PrefixQuery小函数），将Board预处理为char[W*H]，使用非递归方式的DFS（主要维护两个stack）遍历Board实现；
• 二版（~1.6）：在前版基础上，改TST为手写实现的26-way Trie类，Board预处理为Bag<Integer>[W*H]，所有函数都为非递归方式实现（如checklist所要求）；
• 三版（~0.8）：在前版基础上，改非递归方式DFS为递归，将Trie类内容直接写入BoggleSolver，在DFS过程中直接传递Node指针而非调用PrefixQuery函数；
• 终版（0.55）：在前版基础上，全面整理了各步骤细节，cache中间变量，使用Bag而非HashSet存储查询结果，及（参考论坛讨论后）其他细节上的技巧性优化。

很遗憾最终依然没有拿到Bonus，但每一份性能都已是得来不易。

Test 2: timing getAllValidWords() for 5.0 seconds using dictionary-yawl.txt
(must be <= 2x reference solution)

• reference solution calls per second: 6175.83
• student solution calls per second: 11200.52
• reference / student ratio: 0.55

学习经验：

• 开始时其实比较抗拒自己实现一些工具类，如TST或Trie，除了必要的功能外很不愿意改动它们；但当完成前期版本，开始寻求性能优化，实实在在地了解了这些工具类运作机理后，才发现最大的障碍其实来自这些工具类“为通用性而做出的性能上的牺牲”，于是义无反顾地自己手动实现了满足“最低需求”的版本，但因细节尽在自己的掌握，使得在DFS中传递Node指针这样最直接有效的实现方式变得可能，自然，也得到了对应的回报；
• checklist也不是圣经，有独立思考问题的意识才可能发现更大的世界：在实现非递归版DFS时明显感到比较吃力，同时需要追踪维护很多变量，而DFS的逻辑本身也更适合递归；非递归版DFS全当练手，而能够转回递归实现版本则是大胆独立思考的结果；
• 有同学使用多线程达到了非常快的成绩（0.24），但在算法课程作业这个意义上，多线程其实尚处于“灰色区域”，有作弊的嫌疑——况且也没什么技术含量，无须在意。

X. Data Compression与Burrows-Wheeler √ 〇

如果要用一个词来形容这次的作业，我想这个新学的fancy word会再合适不过，“Nifty”。
课程讲到这周基本接近尾声，正则表达式没有作为重点分析太多，而数据压缩，则成为了这最后一次作业的主题；它看似无趣，却在作业细致入微的步骤上隐藏着许多非常精致的点，其间如抽丝拨茧般细腻的过程，堪称快感连连；而其中一个Circular Suffix Array（CSA）排序的实现，可以涵盖从第一部分起讨论过的所有排序算法：题目本身并没有任何限制；学生需要认真比较每一种排序方式的优劣，并选择出其中一种或几种方法的组合，重新制造出一个最适合当前情况下的高效解决方案；在这个意义上，它相比前面的作业，与real world problem更接近了一步。
数据压缩的过程本身就是比较抽象的，而这次的作业说明与checklist更是文字翻倍而全无附图，有同学开始时看不懂题目也是正常，慢慢来啦。【下文所有中括号为题目简短说明，推荐阅读详细说明】

i	Original Suffixes	Sorted Suffixes	index[i]
0	A B R A C A D A B R A !	! A B R A C A D A B R A	11
1	B R A C A D A B R A ! A	A ! A B R A C A D A B R	10
2	R A C A D A B R A ! A B	A B R A ! A B R A C A D	7
*3	A C A D A B R A ! A B R	A B R A C A D A B R A !	*0
4	C A D A B R A ! A B R A	A C A D A B R A ! A B R	3
5	A D A B R A ! A B R A C	A D A B R A ! A B R A C	5
6	D A B R A ! A B R A C A	B R A ! A B R A C A D A	8
7	A B R A ! A B R A C A D	B R A C A D A B R A ! A	1
8	B R A ! A B R A C A D A	C A D A B R A ! A B R A	4
9	R A ! A B R A C A D A B	D A B R A ! A B R A C A	6
10	A ! A B R A C A D A B R	R A ! A B R A C A D A B	9
11	! A B R A C A D A B R A	R A C A D A B R A ! A B	2

【encode部分：对源字符串的CSA（左）排序，返回排好序的CSA（右）的最后一列(ARD!RCAAAABB)，及源字符串所在位置(3)。】
认真阅读作业材料即可大致了解，Burrows-Wheeler压缩算法的三部分：
Huffman压缩已实现不必关心；
Move-to-front编码最为简单可直接实现；
Burrows-Wheeler decoder被称为“the trickest part”，但紧接着便已提示到key-indexed counting与10行的核心代码长度，其实已算是提示了很多；
而其encoding需要使用Circular Suffix Array，所以最大的课题其实是，如何以最高效率实现Circular Suffix Array排序。

下面就先来看CSA的排序问题：
因由源字符串逐个循环偏移构成，CSA是一种具备很多特殊性质的数组，而对这样的数组排序照搬通用的排序算法一定有很大的优化空间没有利用，因此手工打造一个高效实用“特别化”的排序算法，就变成了眼前最实际的问题。
有上一周迭代更新的经验在前，这次几乎是立即开始了手工打造的过程，而可考虑的范围又几乎没有限制，以下是我的几个正确版本：（分数为CSA构造函数运行时间的student / reference ratio（越小越快），均取数据长度为409600的测试成绩作为样本；两个分数仅输入数据不同，第一个为随机ASCII，第二个为典型英文内容(dickens.txt)；满分要求均为3以下）

• 一版（2.85，5.16）：统一使用Mergesort；
• 二版（4.07，6.69）：统一使用Comparator暴力比较（或封装为Comparable类，效率接近）；
• 三版（0.45，1.34）：长度15以下切换到insertion sort，以上使用MSD radix sort；
• 四版（1.29，1.87）：长度15以下切换到insertion sort，以上使用3 way radix quick sort；
• 五版（3.04，3.83）：改编自booksite所附源码，较为低效的ManberMyers实现（使用MSD排好首位字符，接着使用简单quicksort）；

这几个是在权衡利弊后选择实现（如没有选择LSD），并已保证正确性的版本（其中不少的实现使用了algs4.jar源码），可以看出目前相对最高效的方案是MSD+insertion；
因对课堂中提到的ManberMyers算法很感兴趣，所以后期做了不少尝试，但还是没有完全原创地完成一个正确版本，加上还有很多好的选择，这里还会继续努力；
课程API对Java的static块没有要求，所以可以在合适处（如MoveToFront类）利用。

最后是本作业最“Nifty”的部分，Burrows-Wheeler decoder：

i	Sorted Suffixes	next
0	! ? ? ? ? ? ? ? ? ? ? A	3
1	A ? ? ? ? ? ? ? ? ? ? R	0
2	A ? ? ? ? ? ? ? ? ? ? D	6
*3	A ? ? ? ? ? ? ? ? ? ? !	7
4	A ? ? ? ? ? ? ? ? ? ? R	8
5	A ? ? ? ? ? ? ? ? ? ? C	9
6	B ? ? ? ? ? ? ? ? ? ? A	10
7	B ? ? ? ? ? ? ? ? ? ? A	11
8	C ? ? ? ? ? ? ? ? ? ? A	5
9	D ? ? ? ? ? ? ? ? ? ? A	2
10	R ? ? ? ? ? ? ? ? ? ? B	1
11	R ? ? ? ? ? ? ? ? ? ? B	4

【decode部分（层层相扣，建议读原文）：已知CSA最后一列(ARD!...)，与源字符串所在行(3)；对最后一列排序可得第一列(!AAA...)；而next数组使用方式如下：因已知源字符串（排序前第0行）在排序后位置为3，而next[3] = 7，即排序后第7行(B...A)为排序前的第1行（第0行的下一行），可知源字符串第1位为'B'（根据第3行，第0位为‘A’），依此类推即可得到源字符串；next数组的构造为通过比较首尾字符出现位置得到：如第i行末位为A，而首位第一个未标记过的A出现在第j行，则next[i] = j，标记第j行。】
开始时我只看了作业说明，所以冒失地写好了一个“暴力decode”还浑然不自知，直到参考checklist后：“WTF”
事实证明那10行核心代码基本与下图所示相同：

问题的关键在于next数组的构造，可总结为如下几点：

• key-indexed counting核心机理是index的累加，可以保证排序结果的稳定（stable）；
• 根据作业说明的分析，next数组构建的过程，确定重复字符位置的核心机理也是“稳定性”（针对多次出现的同一字符，首尾列的相对先后顺序一致）；
• 对CSA可以不显式创建字符串数组而仅保留源字符串，只添加一个简单的根据offset和index循环获取对应字符的工具函数即可，这为直接使用key-indexed counting创造了非常好的环境。

于是在对源码极简单的改变后，完成了截然不同的任务：(spoiler alert)

for (int i = 0; i < N; i++)
    count[t[i]+1]++;
for (int i = 0; i < 256; i++)
    count[i+1] += count[i];
// The trickiest part
for (int i = 0; i < N; i++)
    next[count[t[i]]++] = i;

其中N为字符串长度，count为计数数组(默认ASCII编码包含256个字符)，next为目标数组，t为已知尾列字符串的对应char[]；（无需显式排序找出首列，第二步count的累加已达到目的）
6行完成了next数组的构建，加上接下来还原源字符串的过程，达到10行。
仔细品读其中内容至理解透彻，相信这妙不可言的感觉一定已深深印在阁下脑海。
欢迎来到算法世界。