matalb学习3-各种求解

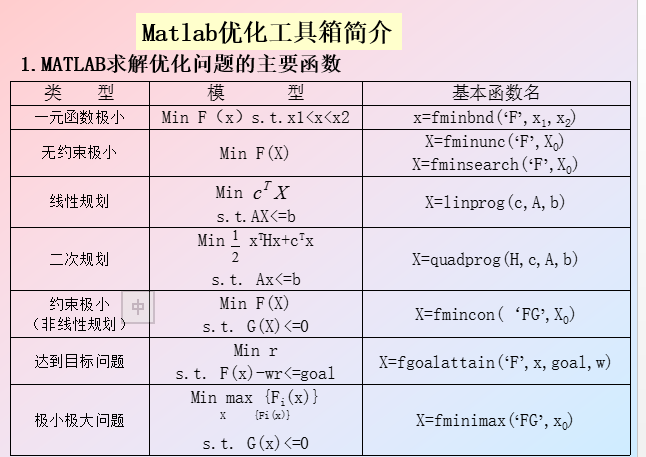
1、解线性规划

linprog解约束类线性规划

c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];
    A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08];
    b=[850;700;100;900];
    Aeq=[]; beq=[];
    vlb=[0;0;0;0;0;0]; vub=[];
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

    c=[6 3 4];
    A=[0 1 0];
    b=[50];
    Aeq=[1 1 1];
    beq=[120];
    vlb=[30,0,20];
    vub=[];             
    [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

f = [13 9 10 11 12 8];
A =  [0.4 1.1 1 0 0 0
      0 0 0 0.5 1.2 1.3];
b = [800; 900];
Aeq=[1 0 0 1 0 0
     0 1 0 0 1 0
     0 0 1 0 0 1];
beq=[400 600 500];
vlb = zeros(6,1);
vub=[];
[x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)

---

2、解无约束类线性规划

用fminbnd(‘函数’，范围)或fminsearch求函数最大值最小值

 f='2*exp(-x).*sin(x)';
        fplot(f,[0,8]);         %作图语句
        [xmin,ymin]=fminbnd (f, 0,8)
        f1='-2*exp(-x).*sin(x)';
        [xmax,ymax]=fminbnd (f1, 0,8)

解多元函数无约束优化，fminunc(函数，范围)求最小值

用mesh画3d图，然后用contour画等高线图

求解：fminsearch

f='100*(x(2)-x(1)^2)^2+(1-x(1))^2';
[x,fval,exitflag,output]=fminsearch(f, [-1.2 2])

求解：
建立函数文件

function f = fun(x)
      y1=((100-x(1)- 0.1*x(2))-(30*exp(-0.015*x(1))+20))*x(1);
      y2=((280-0.2*x(1)- 2*x(2))-(100*exp(-0.02*x(2))+30))*x(2);
      f=-y1-y2;

求解

x0=[50,70];
x=fminunc('fun',x0),
z=fun(x)

---

3、解法常识