1、整数规划-gin都变成整数,要放在end后
max 5x1+8x2
st
x1+x2<6
5x1+9x2<45
end
gin 2!变量变整数使都变成0-1变量,int
@bin,0-1变量限制
2、非线性规划
@bnd(取值范围)
3、复杂问题求解
Model:
Sets: !定义集合;
CK/1..10/:d,y; !10个仓库,y和d都是10维的变量,其中y是01变量,d由下面数据给定;
KH/1..20/; !20个客户;
SS(CK,KH):x,c; !x和c都是10*20的变量,x表示供应百分数,c表示全部供应的费用;
EndSets
Min=@Sum(SS(i,j):c(i,j)*x(i,j))+@Sum(CK(i):d(i)*y(i));
@For(CK(i):@Sum(KH(j):x(i,j))<20*y(i)); !若不建某仓库,是没有物资的;
@For(KH(j):@Sum(CK(i):x(i,j))=1); !每个客户需要供应的百分数之和都为1;
@For(CK(i):@Bin(y(i))); !y是0、1变量限制;
Data: !数据部分;
d=2 3 4 2 3 4 2 3 4 5
;
c=
9 14 6 15 6 19 11 19 4 5 3 6 4 10 12 19 8 7 10 4
10 16 9 12 8 14 4 20 9 13 2 17 18 19 15 18 16 9 8 8
2 10 2 18 4 19 8 13 15 9 4 8 16 2 15 11 8 8 3 14
6 4 1 9 3 3 5 15 6 10 9 13 6 4 8 5 2 9 13 8
7 10 20 17 7 9 13 16 9 15 13 10 12 12 4 16 6 16 6 17
15 18 14 18 11 4 20 20 13 1 10 19 6 4 12 20 20 1 20 7
15 14 20 12 6 15 20 3 1 16 6 6 6 20 3 17 6 11 17 12
1 1 5 2 2 5 16 8 7 7 12 9 5 12 6 4 17 11 11 20
18 16 20 18 5 20 8 6 17 20 9 19 1 10 9 5 8 9 17 15
6 7 17 4 12 4 19 4 13 16 7 6 1 14 11 5 7 9 11 13
;
EndData
End注意:集合定义
如定义di,yi
sets:
CK/1..3/:d,y;
end sets
data:
d=1 3 4;
y=5 7 8;
end data定义di,yi,ci,xi
sets:
a/1..3/:d,y;
b/1..2/;
SS(a,b):c,x;
end sets
data:
d=1 3 4;
y=3 5 7;
c=1 3 4 5 7 8;
x=1 3 3 4 7 8;
end data构造关系式:求和(cij 乘以xij)+求和(di乘以yi)
max=z;
z=@sum(SS(i,j):c(i,j)*x(i,j))+@sum(a(i):d(i)*y(i));@For(a(i):@Sum(b(j):x(i,j))<20*y(i));
@For(b(j):@Sum(a(i):x(i,j))=1);自己建的模型求解
lingo
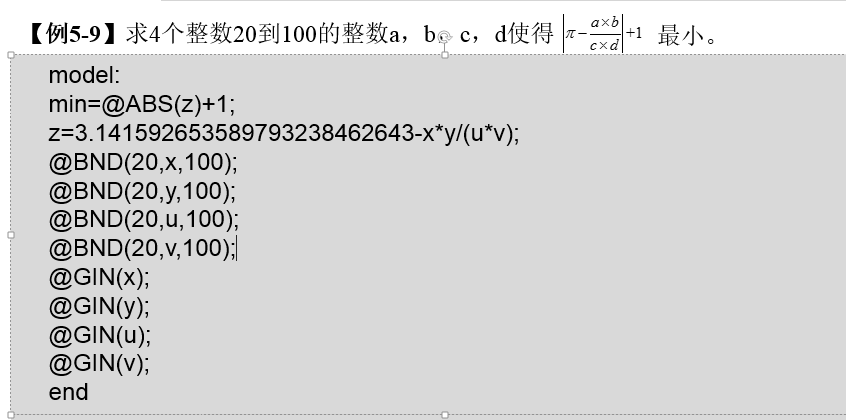
model:
p1=17;
p2=2.67;
k1=0.3;
k2=8;
p3=1700;
N1=550/(1+1.2*@exp(-0.8*x1));
N2=25/(1+1.1*@exp(-0.4*x2));
Max=Z;
Z=k1*p1*N1+k1*p3*N2+(k2-x1-x2)*N1*p2;
0<=x1+x2;x1+x1<=8;
N1>=N2;
0<=x1;x1<=20;
0<=x2;x2<=10;
@gin(x1); @gin(x2);
endmatlab版解非线性规划
构建函数:
function f= con_fun1(x)
p1=17;
p2=2.67;
k1=0.3;
k2=8;
p3=1700;
N1=550/(1+1.2*exp(-0.8*x(1)));
N2=25/(1+1.1*exp(-0.4*x(2)));
f=-1*(k1*p1*N1+k1*p3*N2+(k2-x(1)-x(2))*N1*p2);
endOPTIONS=optimset('display','iter','LargeScale','off');
lb=[0 0];
hb=[20 10];
A=[1 1;-1 -1];
k2=30;
b=[k2;0];
[x,fval,exitflag,output]=fmincon(@con_fun1,[1,1],A,b,[],[],lb,hb,[],OPTIONS);




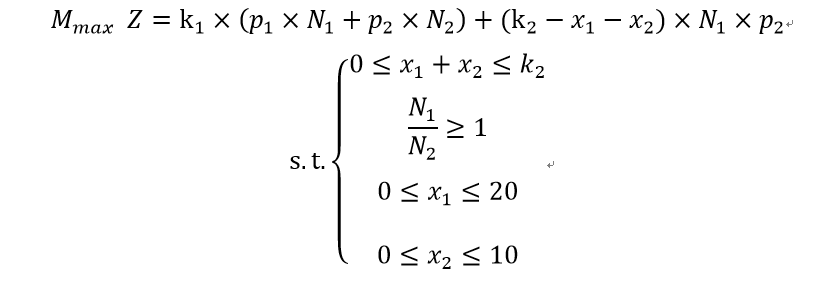

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。