梯度下降法变种的汇总

引言

在各类优化方法中，梯度下降法(Gradient Descent)是最为常见的策略。这里将对一些常见的梯度下降法的变种做一个梳理。方便大家更好地理解梯度下降法的应用域。

如何理解梯度下降法

假想一个状态，你在徒步中准备下山，你该怎么走到谷底？这是一个很显然的问题，你会顺着山梯度（弧度）最大的方向向下走，而并不会选择绕弯。

而梯度下降法其实就是建立在这种十分贪心的企图上，即通过找到梯度最大的方向移动一个固定的距离（一般称为Step Size）。但竟然是贪心，意味着它会有一个问题，如下图所示：如果你正在Starting pt处尝试下山，刚才的策略可能就会让你找到一个Local minima了。这个问题是任何梯度下降法的变种都会遇到的问题。

图片引自 https://thinkingandcomputing....

基本的梯度下降法

梯度下降法可以描述为

$$vec{x}_{n+1} = vec{x}_{n} - alpha f'(vec{x}_{n})$$

其中$f(x)$为所要优化的函数，$alpha$为步长。

叠函数/不动点理论视角下的梯度下降法

我们现在来看梯度下降法的适用条件（为了简单起见，在此只讨论一维的情况）。显然，上面的递推公式即可以转化为一个叠函数数问题，即求：

$$gd(x) = x - alpha f'(x)$$

反复迭代后，收敛的问题。显然，如果$gd(x)$收敛，则收敛于不动点，即不动点$x_0$满足：

$$gd(x_0) = x_0 = x_0 - alpha f'(x_0)$$

化简可得

$$f'(x_0) = 0$$

显然，这个迭代的结果就是函数$f(x)$的极值。现在，我们再来研究梯度下降法的条件。满足该收敛于该不动点的条件是该点为吸引子，即满足

$$|gd'(x)| < 1$$

化简得

$$0 < f''(x) < frac{2}{alpha}$$

显然，$f(x)$必须为凸函数，并在定义域上满足$f''(x) < frac{2}{alpha}$时，梯度下降法才有效。

梯度下降法的一般难题

1. 步长的选择

2. 不是凸函数

坐标下降法

坐标下降法（Coordinate descent）的策略相对而言是一种降低计算复杂度的方式，方法是每次只下降一个方向（坐标）的值。

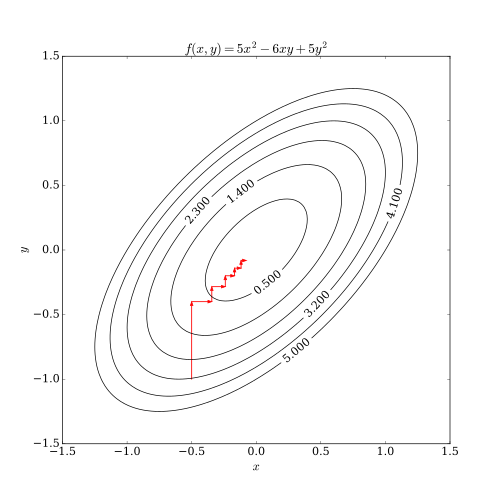
图片来自Wikipedia。

按是否设置步长可以分为两种。

含步长的坐标下降法

步骤：

• Choose an initial parameter vector x.

• Until convergence is reached, or for some fixed number of iterations:

  • Choose an index i from 1 to n.

  • Choose a step size α.

  • Update x_i to x_i − α * ∂F/∂x_i(x).

不含步长的坐标下降法

此外，坐标下降法的另一个非常好的迭代方法是，在迭代一个x_i时，可以固定其他x的前提下，只计算$f(x_i) = F(x)$。此时，计算复杂度降低，且迭代速度也可以相对加快。

步骤：

• Choose an initial parameter vector x.

• Until convergence is reached, or for some fixed number of iterations:

  • Choose an index i from 1 to n.

  • Update x_i to x_min, where (argmin F(x_i|x_n fixed but x_i)) = F(x_min)

坐标下降法的限制

坐标下降法在应对非平滑函数时会有很大的局限，如下图：

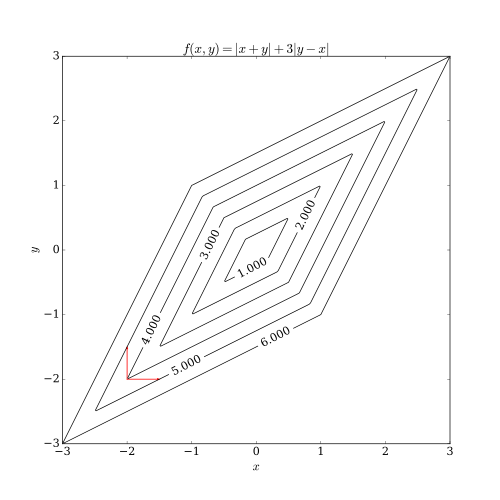
最后会在红线交汇处就停止迭代了。

随机梯度下降法/批梯度下降法

在实际3V大数据场景时，会遇到一个常见问题，因为样本数N的数量过大，导致每次迭代的计算代价非常大；并且如果做一个实时的训练模型，显然，每次有新数据读入时，样本数都会增加，每次迭代的速度也会越来越慢。

因此，一个比较好的策略就是随机梯度下降法（Stochastic gradient descent），即一次迭代只迭代一个样本。这样做的好处是显然的，但是，无法规避的，每次迭代loss function的变异就会很大，如下图：

这样，显然收敛的方向是不定的，而且，很可能收敛速度非常慢。

一个有效的替代方案是，每次迭代的样本数增加到一个很小的数量（通常被称为Mini-Batch），这样，有可以有效地增加收敛速度，这种方案也被称为批梯度下降法（(Mini-)Batch gradient descent）。当Batch的数量增加时，模型的收敛速度加快，但是训练速度会降低。

问题

1. 在训练样本时，采用此种方案之前必须保证数据是没有任何顺序特征的，不然，会对训练产生极大影响。

2. 训练的模型并非是最后一次迭代时训练的结果最优，此时要注意采用一定策略选择最优模型。

总结

类别	梯度下降	坐标下降	随机梯度下降/批梯度下降
场景	基本场景、小数据	feature较多，平滑函数	大数据、实时训练
策略	寻找最大梯度方向，迭代	每次只迭代一个坐标	每次只迭代一（k < N）个样本
缺点	步长选择，在维度、样本量过大时速度较慢	非平缓函数失效	收敛具有一定的随机性