首先我们需要明确一个概念,我们讨论的线性或者非线性针对的是自变量的系数,而非自变量本身,所以这样的话不管自变量如何变化,自变量的系数如果符合线性我们就说这是线性的。所以这里我们也就可以描述一下多项式线性回归。
由此公式我们可以看出,自变量只有一个,就是x,只不过x的级数(degree)不同而已。
我们这次用的数据是公司内部不同的promotion level所对应的薪资
下面我们来看一下在Python中是如何实现的
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:2].values
# 这里注意:1:2其实只有第一列,与1 的区别是这表示的是一个matrix矩阵,而非单一向量。
y = dataset.iloc[:, 2].values接下来,进入正题,开始多项式线性回归:
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree = 1) #degree 就是自变量需要的维度
X_poly = poly_reg.fit_transform(X)
lin_reg_2 = LinearRegression()
lin_reg_2.fit(X_poly, y)这个过程我们设置了一元一次的自变量:degree=1 意思是自变量只有一次,相当于简单线性回归
我们在图像中表示一下:
# 图像中显示
plt.scatter(X, y, color = 'red')
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
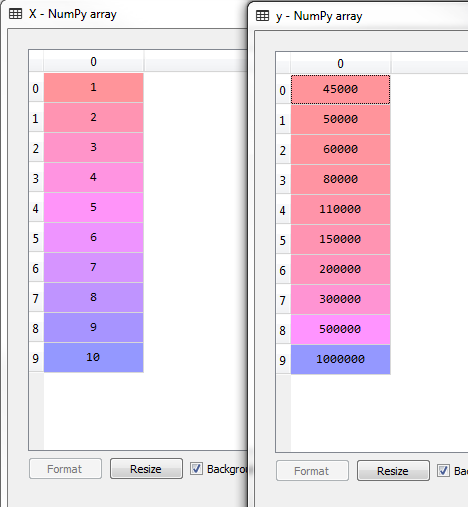
plt.show()此图像与用简单线性回归表示的图像是一样的
# 简单线性回归 图像中显示
plt.scatter(X, y, color = 'red')
plt.plot(X, lin_reg.predict(X), color = 'blue')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
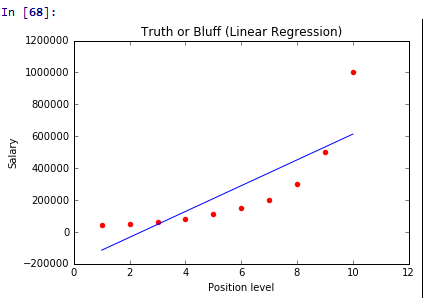
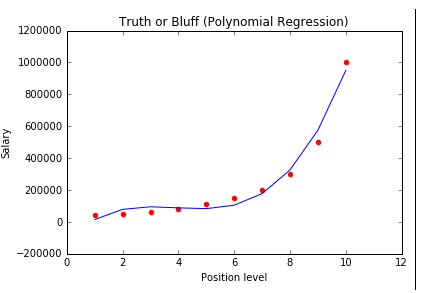
plt.show()下面我们试着改变一下维度,将degree设置成2,其他不改变,执行一下代码看看图像:
我们可以发现整个趋势符合数据的分布。
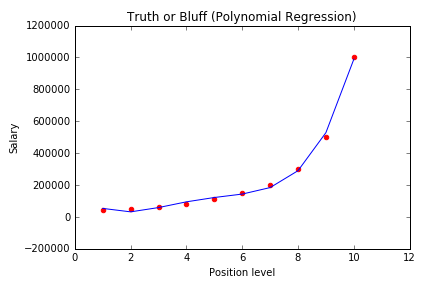
我们将degree改成3 和 4 看看结果
我们可以发现,当degree=4的时候,基本上已经符合所有点的分布了
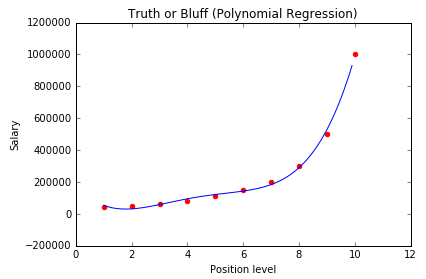
我们通过拆分横坐标将图像变得平滑一些:
X_grid = np.arange(min(X), max(X), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, lin_reg_2.predict(poly_reg.fit_transform(X_grid)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
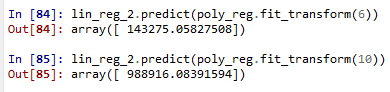
plt.show()下面我们给出一个测试值来试试结果 (6,10)
lin_reg_2.predict(poly_reg.fit_transform(6))
lin_reg_2.predict(poly_reg.fit_transform(10))与实际值还是比较接近的。
一下是R的代码
dataset = read.csv('Position_Salaries.csv')
dataset = dataset[2:3]
lin_reg = lm(formula = Salary ~ .,
data = dataset)
# 将多项式线性回归fit数据集
dataset$Level2 = dataset$Level^2
dataset$Level3 = dataset$Level^3
dataset$Level4 = dataset$Level^4
poly_reg = lm(formula = Salary ~ .,
data = dataset)
library(ggplot2)
ggplot() +
geom_point(aes(x = dataset$Level, y = dataset$Salary),
colour = 'red') +
geom_line(aes(x = dataset$Level, y = predict(lin_reg, newdata = dataset)),
colour = 'blue') +
ggtitle('Truth or Bluff (Linear Regression)') +
xlab('Level') +
ylab('Salary')
# install.packages('ggplot2')
library(ggplot2)
ggplot() +
geom_point(aes(x = dataset$Level, y = dataset$Salary),
colour = 'red') +
geom_line(aes(x = dataset$Level, y = predict(poly_reg, newdata = dataset)),
colour = 'blue') +
ggtitle('Truth or Bluff (Polynomial Regression)') +
xlab('Level') +
ylab('Salary')
# install.packages('ggplot2')
library(ggplot2)
x_grid = seq(min(dataset$Level), max(dataset$Level), 0.1)
ggplot() +
geom_point(aes(x = dataset$Level, y = dataset$Salary),
colour = 'red') +
geom_line(aes(x = x_grid, y = predict(poly_reg,
newdata = data.frame(Level = x_grid,
Level2 = x_grid^2,
Level3 = x_grid^3,
Level4 = x_grid^4))),
colour = 'blue') +
ggtitle('Truth or Bluff (Polynomial Regression)') +
xlab('Level') +
ylab('Salary')
# 预测新的数据
predict(lin_reg, data.frame(Level = 6.5))
summaryss(poly_reg)我们可以看到模型的系数之间的关系
后面还有还有决策树和森林回归,这样线性回归就写完了,我争取这几天写完,前几天准备申请研究生的writing sample,关于数据库index做了一些,在合适的时候 我会把文章放出来,谢谢大家~~希望大家多多推荐
--E·O·F--
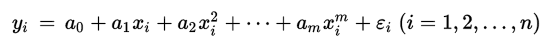


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。