Javascript 作为一门动态语言,其数字类型只有 number 一种。 nubmer 类型使用的就是 IEEE754 标准中的 双精度浮点数。Javascript 数字的许多特性都依赖于此标准,例如令人费解的 0.1+0.2不等于0.3
这篇文章介绍 IEEE754 标准中双精度浮点数二进制储存格式,并由此推出 js 中数字的一些特性。
一、IEEE754 中浮点数的储存格式
在 IEEE754 中,双精度浮点数储存为64位:
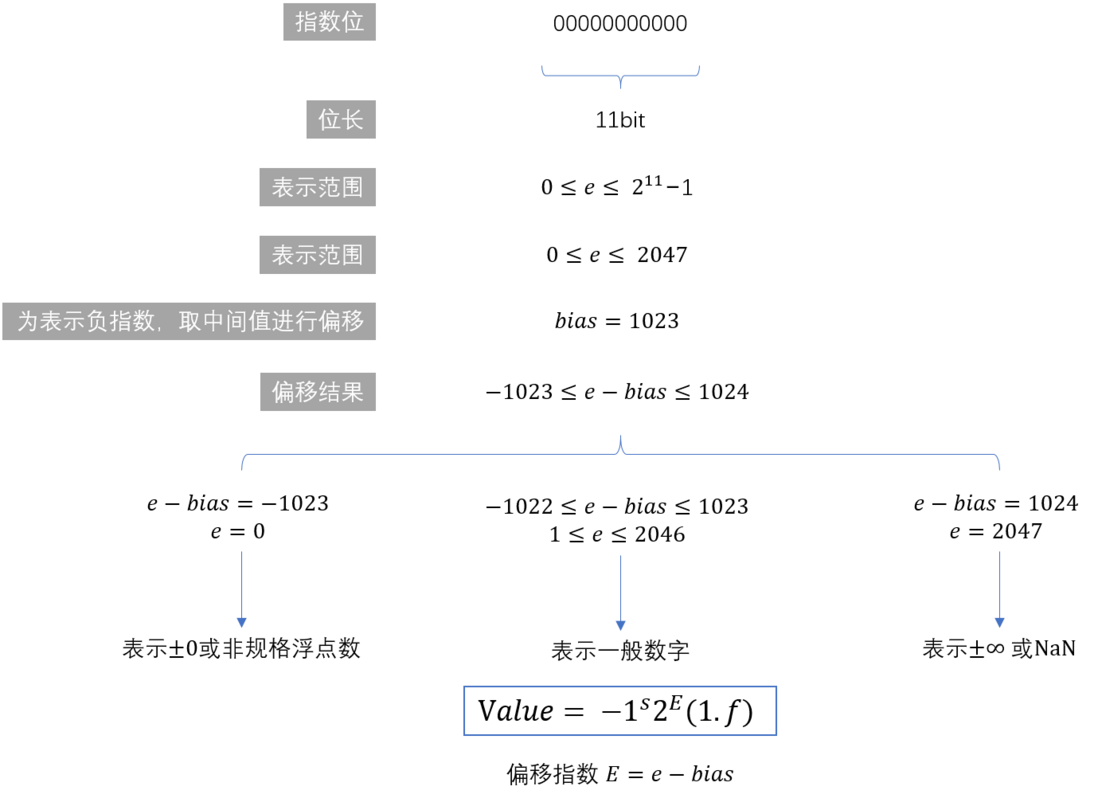
指数位可以通过下面的方法转换为使用的指数值:
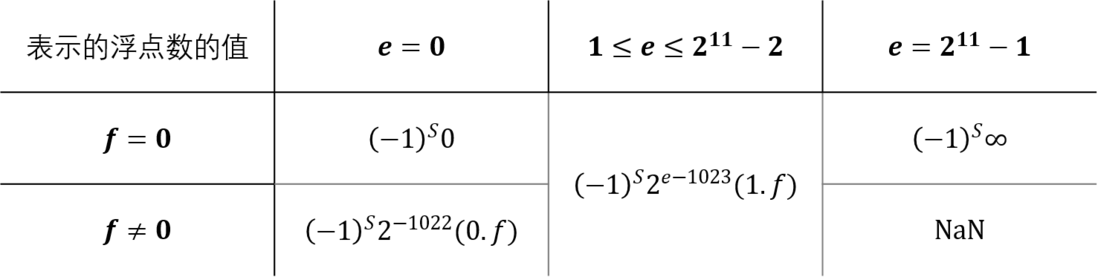
浮点数表示的值的形式由 $e$ 和 $f$ 确定:
二、根据 IEEE754 计算 0.1+0.2
1. 将 0.1 使用转换为二进制
$0.1 = (0.0\dot0\dot0\dot1\dot1)_2=(-1)^0\times2^{-4}\times(1.\dot1\dot0\dot0\dot1)_2$
$0.2 = 0.1\times2^1=(-1)^0\times2^{-3}\times(1.\dot1\dot0\dot0\dot1)_2$
由于小数位 $f$ 仅储存 52bit, 储存时会将超出精度部分进行"零舍一入"
| 值类型 | 小数位(储存范围内) | 小数位(储存范围外) |
|---|---|---|
| 无限精确值 | 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 | 1001 1001... |
| 实际储存值 | 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 | - |
由于计算加减时不会对指数位进行位运算,这里不计算指数位的表示,直接使用数字表示最终的指数值
0.1、0.2 的表示如下:
| 浮点数数值 | 符号位 $s$ | 指数值 $E$ | 小数位 $f$ |
|---|---|---|---|
| 0.1 | 0 | -4 | 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 |
| 0.2 | 0 | -3 | 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010 |
2. 将 0.1 与 0.2 相加
在计算浮点数相加时需要先进行“对位”,将较小的指数化为较大的指数,并将小数部分相应右移
$0.1 \rightarrow (-1)^0\times2^{-3}\times(0.1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1101 0)_2$
$0.2 \rightarrow (-1)^0\times2^{-3}\times(1.1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010)_2$
$0.1 + 0.2 = (-1)^0\times2^{-2}\times(1.0011001100110011001100110011001100110011001100110100)_2$
可以通过下面的方法检验计算结果是否于 js 中一致:
0.1 + 0.2 === (-1)**0 * 2**-2 * (0b10011001100110011001100110011001100110011001100110100 * 2**-52)
//> true
//计算正确三、计算 javascript Number 的特性
在js中 Number对象上附带了许多属性,表示可数的范围等信息,例如 Number.MAX_SAFE_INTEGER 是一个16位的数字,这一部分将解释如何计算出这些有特殊意义的数字。
1.计算 Number.MAX_VALUE 和 Number.MIN_VALUE
当符号位为0、指数取到1023、小数位全为1时,为可表示的最大值
当符号位为0、指数位全为0(表示非规格浮点数)、小数位仅最后一位为1时,为可表示的最小正值
var max = (-1)**0 * 2**1023 * (Number.parseInt( "1".repeat(53) ,2) * 2**-52);
max === Number.MAX_VALUE;
//> true
var min = (-1)**0 * 2**-1022 * (Number.parseInt( "0".repeat(52)+"1" ,2) * 2**-52);
min === Number.MIN_VALUE;
//> true2.计算 Number.MAX_SAFE_INTEGER 和 Number.MIN_SAFE_INTEGER
Number.MAX_SAFE_INTEGER 表示最大安全整数,它是9开头的16位数字,也表明js number最大精度不超过16位。
ECMASCRIPT-262 定义:
The value of Number.MAX_SAFE_INTEGER is the largest integer n such that n and n + 1 are both exactly representable as a Number value.
http://www.ecma-international...
改变指数位为53,这让每个小数位都表示浮点数的整数部分,小数位最低位对应 $2^0$,然后将每个小数位都置1,可得最大准确整数:
var max_safe_int = (-1)**0 * 2**52 * (Number.parseInt("1".repeat(53),2) * 2**-52);
max_safe_int === Number.MAX_SAFE_INTEGER;
//> true
//当它 +1 时,可由 (-1)**0 * 2**53 * (Number.parseInt("1"+"0".repeat(52),2) * 2**-52) 正确表示,而再 +1 时则无法准确表示
//符号位取反可得最小安全整数
-1 * max_safe_int === Number.MIN_SAFE_INTEGER;3.计算 Number.EPSILON
Number.EPSILON 是一个极小值,用于检测计算结果是否在误差范围内。例如:
Math.abs(0.1 + 0.2 - 0.3) < Number.EPSILON;
//> true
//2017-9-27 补充
1.1 + 1.3 - 2.4 < Number.EPSILON
//> false根据 ECMASCRIPT-262 定义:
The value of Number.EPSILON is the difference between 1 and the smallest value greater than 1 that is representable as a Number value, which is approximately 2.2204460492503130808472633361816 x 10−16.
http://www.ecma-international...
根据定义Number.EPSILON是大于1的最小可表示数与1的差,可以据此计算出 Number.EPSILON 的值:
//将表示1的二进制小数位的最左端置1,可表示大于1的最小数
var epsilon = (-1)**0 * 2**0 * (Number.parseInt("1"+"0".repeat(51)+"1",2) * 2**-52) - 1;
// (-1)**0 * 2**0 * (+`0b1${"0".repeat(51)}1` * 2**-52) - 1;
epsilon === Number.EPSILON;
//> true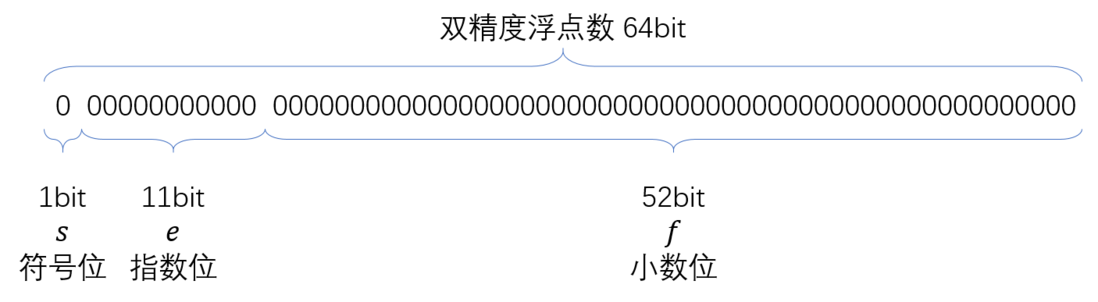


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。