数据结构与算法：图和图算法(一)

摘 要 ： 图 论 问 题(Graph Theory)

• 节点(Vertex) 与 边（Edge）

• 图的表示： 邻接表 和 邻接矩阵

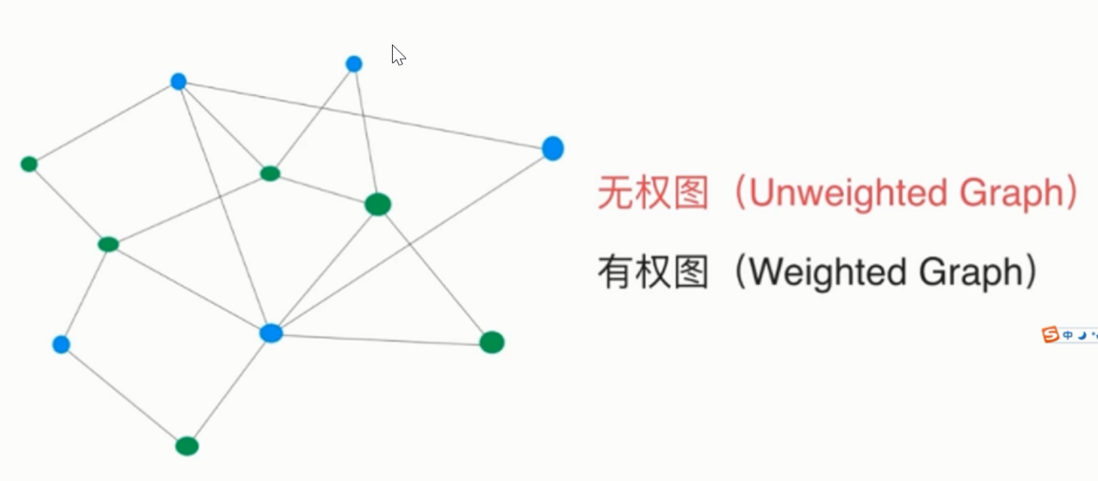
  • 这里可以分为 有向图 和无向图
无向图是一种特殊的有向图
  • 有权图 和 无权图
• 图的遍历： DFS BFS 常见可以解决的问题有： 联通分量 Flood Fill 寻路 走迷宫 迷宫生成 无权图的最短路径 环的判断
• 最小生成树问题（Minimum Spanning Tree） Prim Kruskal
• 最短路径问题(Shortest Path) Dijkstra Bellman-Ford
• 拓扑排序(Topological sorting)

这里可演示　－> https://mrpandey.github.io/d3...

图

什么是图？

图是一种复杂的非线性结构。

在线性结构中，数据元素之间满足唯一的线性关系，每个数据元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继；

在树形结构中，数据元素之间有着明显的层次关系，并且每个数据元素只与上一层中的一个元素(parent node)及下一层的多个元素(孩子节点)相关；

而在图形结构中，节点之间的关系是任意的，图中任意两个数据元素之间都有可能相关。

图G由两个集合V(顶点Vertex)和E(边Edge)组成，定义为G=(V，E)

无向图 和 有向图

相关基础戳这里

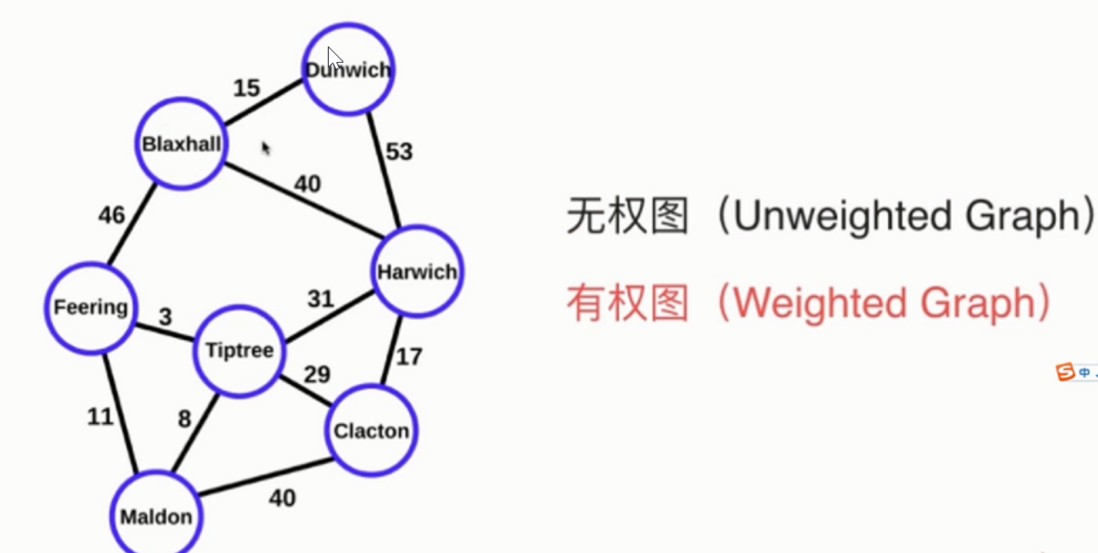
有权图 和 无权图

顶点的度

对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。比如，图(a)无向图中顶点V3的度D(V3)=3

对于有向图，顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。比如，顶点V1的入度ID(V1)=1，出度OD(V1)=2，所以D(V1)=ID(V1)+OD(V1)=1+2=3

记住，不管是无向图还是有向图，顶点数n，边数e和顶点的度数有如下关系：

因此，就拿有向图(b)来举例，由公式可以得到图G的边数e=(D(V1)+D(V2)+D(V3))/2=(3+2+3)/2=4

路径、路径长度和回路

路径，比如在无向图G中，存在一个顶点序列Vp,Vi1,Vi2,Vi3…，Vim，Vq，使得(Vp,Vi1)，(Vi1,Vi2)，…,(Vim,Vq)均属于边集E(G)，则称顶点Vp到Vq存在一条路径。

一系列顶点构成路径，路径中所有顶点都由边连接。

路径长度，是指一条路径上经过的边的数量。

回路，指一条路径的起点和终点为同一个顶点。

用图对现实中的系统建模

可以用图对现实中许多系统建模。

比如对交通流量建模，顶点可以表示街道的十字路口，边表示街道。加权的边可以表示限速或者车道的数量。建模人员可以用这个系统来判断最佳路线及最有可能堵车的街道。

任何运输系统都可以用图来建模。比如，航空公司可以用图来为其飞行系统建模。将每个机场看成顶点，将经过两个顶点的每条航线看作一条边。加权的边可以看作从一个机场到另一个机场的航班成本，或两个机场之间的距离，这取决与建模的对象是什么。

包含局域网和广域网（如互联网）在内的计算机网络，同样经常用图来建模。

另一个可以用图来建模的实现系统是消费市场，顶点可以用来表示供应商和消费者。

图的创建和遍历

图的两种存储结构（表示图）

乍看起来，图和树或者二叉树很像，我们可能会尝试用树的方式来创建一个图类，用节点来表示每个顶点。但这种情况下，如果用基于对象的方式去处理就会有问题，因为图可能增长到非常大。 用对象来表示图很快会变得效率低下，所以我们要考虑表示顶点或边的其他方案。

表示顶点

创建图类的第一步是要创建一个Vertex类保存顶点和边。这个类的作用与链表和二叉搜索树的Node类一样。Vertex类有两个数据成员： 一个用于标识顶点，另一个是表示这个顶点是否被访问过的布尔值。分别命名为label 和 wasVisited.这个类只需要一个函数，那就是为顶点的数据成员设定值的构造函数。

//Vertex 类

function Vertex (label wasVisited) {
  this.label = label;
  this.wasVisited = wasVisited;
}

我们将所有顶点保存到数组中，在图类里，可以通过它们在数组中位置引用它们。

表示边

图的实际信息都保存在边上，因为它们描述了图的结构。我们容易像之前提到的那样用二叉树的方式去表示图，这是不对的。二叉树的表现形式相当固定，一个父节点只能有两个子节点，而图结构却要灵活的多，一个顶点既可以有一条边，也可以有多条边与它相连。

我们将表示图的边的方法称为邻接表 或者邻接表数组。

这种方法将边储存为由顶点的相邻顶点列表构成的数组，并以此顶点作为索引。

当我们在程序中引用一个顶点时，可以高效地访问与这个顶点相连的所有顶点的列表。

邻接矩阵

原理就是用两个数组，一个数组保存顶点集，一个数组保存边集。下面的算法实现里边我们也是采用这种存储结构。如下图所示：

邻接表

邻接表是图的一种链式存储结构。这种存储结构类似于树的孩子链表。对于图G中每个顶点Vi，把所有邻接于Vi的顶点Vj链成一个单链表，这个单链表称为顶点Vi的邻接表。

构建图

确定了如何在代码中表图之后，构建一个表示图的类就容易了，下面是一个Graph类的定义：

function Graph (v) {
  this.vertices = v;
  this.edges = 0;
  this.adj = [];
  for (var i = 0; i < this.vertices; ++i) {
    this.adj[i] = [];
    this.adj[i].push("");
  }
  this.addEdge = addEdge;
  this.toString = toString;
}

这个类会记录一个图表示了多少条边，并使用一个长度与图的顶点数相同的数组来记录顶点数量。
通过for循环为数组中的每个元素添加一个子数组来储存所有的相邻顶点，并将所有元素初始化为空字符串。

//addEdge()  函数定义如下
 function addEdge(v,w) {
  this.adj[v].push(w);
  this.adj[w].push(v);
  this.edges++;
}

当调用这个函数并传入顶点A 和 B 时，函数会先查找顶点A ，函数会先查找A的邻接表，将顶点B添加到列表中，然后再查找顶点B的邻接表，将顶点A加入列表。最后，这个函数会将边数加 1.

showGraph() 函数会通过打印所有顶点及其相邻顶点列表的方式来显示图：

 function showGraph() {
  for (var i = 0 ; i < this.vertices; ++i ) {
  putstr(i + "->");
      for (var j  = 0; j < this.vertices; ++j) {
        if(this.adj[i][j] != undefined)
          putstr(this.adj[i][j] + ' ')
      }
      
      print();
  
  }
}

一个完整的 Graph 类

function Graph(v) {
  this.vertices = v ;
  this.edges = 0;
  this.adj = [];
  for(var i = 0 ; i < this.vertices; ++i ){
    this.adj[i] = [];
    this.adj[i].push("");
    }
  this.addEdge = addEadge;
  this.showGraph = showGraph;
}

function addEdge(v,w)  {
  this.adj[v].push(w);
  this.adj[w].push(v);
  this.edges++;
}

function showGraph () {
  for (var i = 0; i < this.vertices; ++i) {
  putstr(i + " -> ");
  for (var j = 0; j < this.vertices; ++j) {
    if(this.adj[i][j] != undefined) {
      putstr(this.adj[i][j] + ' ');
    }
  }
  print()
  }
}

图的两种遍历方法

确定从一个指定的顶点可以到达其他哪些顶点。这是经常对图执行的操作。我们可能想通过地图了解到从一个城镇到另一个城镇有哪些路，或者从一个机场到其他机场有哪些航班。

而图上这些操作是用算法执行的。在图上可以执行以下两种遍历算法用于搜索：

深度优先搜索遍历

深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是：

a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。

b)然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。

c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。

简单的来说，深度优先搜索包括从一条路径的起始点开始追溯，直到到达最后一个顶点，然后回溯，继续追溯下一条路径，直到到达最后的顶点，如此往复，直到没有路径为止

这不是在搜索特定的路径，而是通过搜索来查看在图中有哪些路径可以选择。

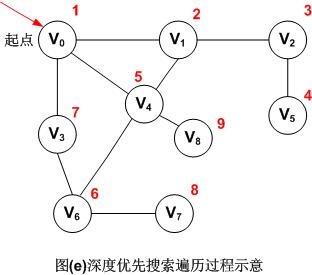
图示如下：

注：红色数字代表遍历的先后顺序，所以图(e)无向图的深度优先遍历的顶点访问序列为：V0，V1，V2，V5，V4，V6，V3，V7，V8

如果采用邻接矩阵存储，则时间复杂度为O(n2)；当采用邻接表时时间复杂度为O(n+e)。

深度优先搜索的算法比较简单： 访问一个没有访问过的顶点，将它标记为已访问，再递归地去访问在起始点的邻接表中其他没有访问过的顶点。

要让该算法运行，需要为Graph类添加一个数组，用来储存已访问过的顶点，将它所有元素的值全部初始化为false。Graph类的代码片段演示了这个新数组及其初始化过程：

this.marked = [];
for(var i = 0; i < this.vertices; ++i) {
  this.marked[i] = false;
}

现在我们可以开始编写深度优先搜索函数：

function dfs(v) {
  this.marked[v] = true;
  //用于输出的if语句在这里不是必须的
  if(this.adj[v] != undefined)
    print("Visited vertex: " + v)
  for each(var w in this.adj[v]) {
   if(!this.marked[w]) {
     this.dfs(w);
   }
  }
}

代码中用到了print()函数，这样我们可以查看当前正在访问的顶点。当然，dfs()不想要print()也能运行。

注意 深度优先算法属于盲目搜索，无法保证搜索到的路径为最短路径。

执行深度优先搜索

下面是depthFirst() 函数 及完整的Graph类定义

 function Graph(v) {
  this.vertices = v;
  this.edges = 0;
  this.adj = [];
  for(var i=0;i<this.vertices;i++) {
    this.adj[i] = [];
    this.adj[i].push("");
  }
  this.addEdge = addEdge;
  this.showGragh = showGragh;
  this.dfs = dfs;
  this.marked = [];
  for(var i=0;i<this.vertices;i++){
  this.marked[i] = false; 
  }
}

function addEdge(v,w) {
  this.adj[v].push(w);
  this.adj[w].push(v);
  this.edges++;
}

function showGragh() {
  for(var i = 0;i < this.vertices; ++i) {
  putstr(i + "->");
    for(var j=0;j<this.vertices;++i) {
      if(this.adj[i][j] != undefined)
        putstr(this.add[i][j] + ' ');
    }
    print();
  }
}

function dfs(v) {
  this.marked[v] = true;
  if(this.adj[v]!==undefined){
  print("Visited vertex: " + v);
  }
  for each(var w in this.adj[v]) {
    if(!this.marked[w]) {
      this.dfs(w)
    }
  }
}

// 测试dfs() 函数
load("Graph.js");
g = new Gragh(5);
g.addEdge(0,1);
g.addEdge(0,2);
g.addEdge(1,3);
g.addEdge(2,4);
g.showGragh();
g.dfs(0);

以上程序的输出结果：

0 -> 1 2
1 -> 0 3
2 -> 0 4
3 -> 1
4 -> 2

Visited vertex: 0 
Visited vertex: 1
Visited vertex: 2 
Visited vertex: 3 
Visited vertex: 4

完整示例

戳这里

广度优先搜索遍历

广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是：

a) 首先访问出发点Vi

b) 接着依次访问Vi的所有未被访问过的邻接点Vi1，Vi2，Vi3，…，Vit并均标记为已访问过。

c) 然后再按照Vi1，Vi2，… ，Vit的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。
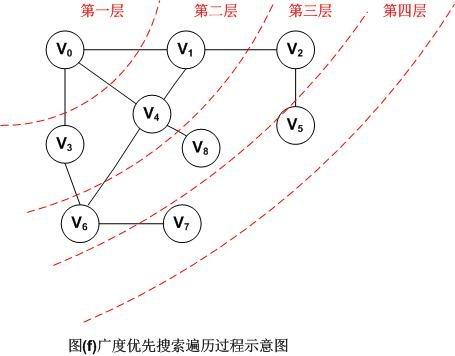
图示如下：

因此，图(f)采用广义优先搜索遍历以V0为出发点的顶点序列为：V0，V1，V3，V4，V2，V6，V8，V5，V7

如果采用邻接矩阵存储，则时间复杂度为O(n2)，若采用邻接表，则时间复杂度为O(n+e)。

简单的来说，广度优先搜索从一个顶点开始，尝试访问尽可能靠近它的顶点。本质上这种搜索在图上是逐层移动的，首先检查最靠近第一个顶点的层，再逐渐向下移动到离起始顶点最远的层

广度优先搜索算法使用了抽象的队列而不是数组来对已经访问过的顶点进行排序。算法工作原理如下：

1. 查找与当前顶点相邻的未访问顶点，将其添加到已访问顶点列表及队列中;
2. 从图中取下一个顶点v，添加到已访问的顶点列表
3. 将所有与v相邻的未访问顶点添加到队列。

function bfs(s) {
  var queue = [];
  this.marked[s] = true;
  queue.push(s); // 添加到队尾
  while (queue.length > 0) {
    var v =queue.shift(); //从队首移除
    if(this.adj[v]!= undefined) {
      print("Visisted  vertex: " + v);
    } 
    for each(var w in this.adj[v]) {
      if(!this.marked[w]) {
        this.marked[w] = true;
        queue.push(w);
      }
    }
  }
}

执行广度优先搜索

load("Graph.js");
g = new Graph(5);
g.addEdge(0,1);
g.addEdge(0,2);
g.addEdge(1,3);
g.addEdge(2,4);
g.showGragh();
g.bfs(0);

以上程序的输出结果：

0 -> 1 2
1 -> 0 3
2 -> 0 4
3 -> 1
4 -> 2
Visited vertex: 0
Visited vertex: 1
Visited vertex: 2
Visited vertex: 3
Visited vertex: 4

关于广度优先遍历的应用
-> d3中的each()api node.each(function)

查找最短路径

图最常见的操作之一就是寻找从一个顶点到另一个顶点的最短路径.
考虑下面的例子：

假期中，你将在两个星期的时间里游历10个旅游城市，去那里最富盛名的景点（1 个），你希望通过最短路径算法，找出开车游历10个城市行驶的最小历程数。
另一个最短路径问题涉及创建一个计算机网络时的开销，其中包括两台电脑之间传递数据的时间，或者两台电脑建立和维护连接的成本。
最短路径算法可以帮助确定构建此网络的最有效方法。

广度优先搜索对应的最短路径

在执行广度优先搜索时，会自动查找从一个顶点到另一个相邻顶点的最短路径。
例如：要查找从顶点A到顶点D的最短路径，我们首先会查找从A到D是否有任何一条单边路径，接着查找两条边的路径，以此类推。这正是广度优先搜索的搜索过程，因此我们可以轻松地修改广度优先搜索算法，找出最短路径。

确定路径

要查找最短路径，需要修改广度优先搜索算法来记录从一个顶点到另一个顶点的路径，这需要对Gragh类做一些修改。

首先，需要一个数组来保存从一个顶点到下一个顶点的所有边。我们将这个数组命名为edgeTo。 因为从始至终使用的都是广度优先搜索函数，所以每次都会遇到一个没有标记的顶点，除了对它进行标记外，还会从邻接列表中我们正在搜索的那个顶点添加一条边到这个顶点。
下面是新的bfs()函数 和需要添加到Gragh类的代码：

//将这行添加到Gragh类
this.edgeTo = [];

// bfs函数

function bfs(s) {
  var queque = [];
  this.marked[s] = true;
  queue.push(s); //添加到队尾
  while (queue.length > 0 ) {
   var v = queque.shift(); //从队首移除
   if(v == undefined) {
     print("Visited vertex: " + v);
   }
   for each(var w in this.adj[v]) {
     if(!this.marked[w]) {
       this.edgeTo[w] = v;
       this.marked[w] = true;
       queue.push(w);
     }
   }
  }
}

现在我们需要一个函数，用于展示图中连接到不同顶点的路径。函数pathTo() 创建了一个栈，用来储存与指定顶点有共同边的所有顶点。
以下是pathTo()函数的代码，以及一个简单的辅助函数：

function pathTo(v) {
  var source = 0;
  if(!this.hasPathTo(v) {
    return undefined;
  }
  var path = [];
  for (var i = v; i!= source;i = this.edgeTo[i]) {
    path.push(i);
  }
  path.push(source);
  return path;
}

function hasPathTo(v) {
  return this.marked[v];
}

需要确保将以下声明添加到 Graph()构造函数中：

this.pathTo = pathTo;
this.hasPathTo = hasPathTo;

有了这个函数，我们要做的就是编写一些客户端代码来显示从源顶点到某个特定顶点的最短路径。

查找一个顶点的最短路径

load("Gragh.js");
g = new Gragh(5);
g.bfs(0);
g.addEdge(0,1);
g.addEdge(0,2);
g.addEdge(1,3);
g.addEdge(2,4);
var vartex = 4;
var paths = g.pathTo(vertex);
while (paths.length > 0) {
  id(paths.length > 1) {
    putstr(paths.pop() + '-');
  }
  else {
    putstr(paths.pop());
  }
}

以上程序输出结果为：

0-2-4

也就是从顶点 0 到顶点4 的最短路径

拓扑排序

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。
该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

它是一个 DAG 图，那么如何写出它的拓扑排序呢？这里说一种比较常用的方法：

1. 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。

通常，一个有向无环图可以有一个或多个拓扑排序序列。

拓扑排序的应用

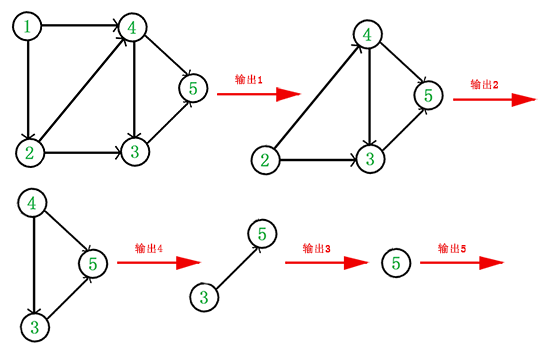
拓扑排序通常用来“排序”具有依赖关系的任务。它与深度优先搜索BFS类似。不同的是，拓扑排序算法不会立即输出已访问的顶点，而是访问当前顶点邻接表中的所有相邻顶点，直到这个列表穷尽时，才将当前顶点压入栈中。
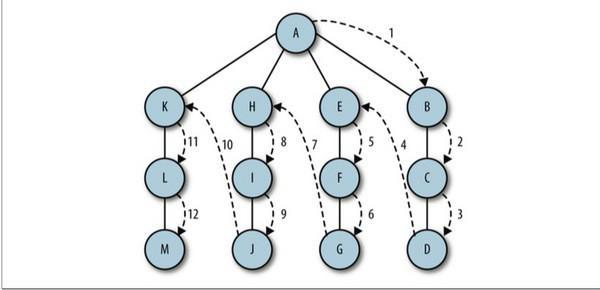
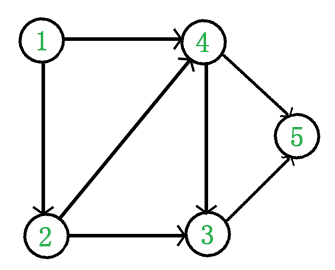
举一个例子如下图：

其拓扑排序可以是：

     1,2,3,4,5,7,9,10,11,6,12,8

也可以是：

     9,10,11,6,1,12,4,2,3,5,7,8

再比如，如果用一个DAG图来表示一个工程，其中每个顶点表示工程中的一个任务，用有向边<A,B>表示在做任务 B 之前必须先完成任务 A。故在这个工程中，任意两个任务要么具有确定的先后关系，要么是没有关系，绝对不存在互相矛盾的关系（即环路）。

graph-data-structure

其他经典问题

• 有向图周期检测：
• 强连通组件图

以上不少内容来自《数据结构与算法 javascript》这本书
,感觉讲的很糟糕 ,也有可能是译者的问题。 回头翻一翻其他资料 重新整理下 并且补上相关算法的应用代码

常见问题

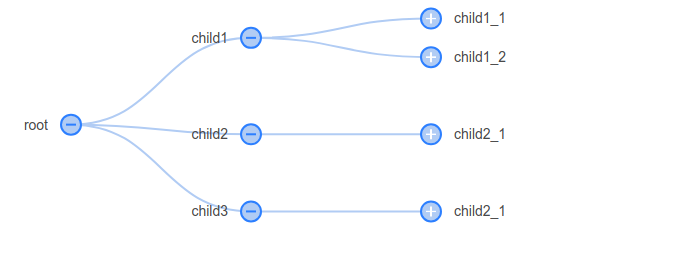
分别用广度优先遍历和深度优先遍历展开下面节点

var tree = {
    name: 'root',
    children: [{
        name: 'child1',
        children: [{
            name: 'child1_1',
            children: []
        }, { name: 'child1_2', children: [] }]
    }, {
        name: 'child2',
        children: [{
            name: 'child2_1',
            children: []
        }]
    }, {
        name: 'child3',
        children: [{
            name: 'child2_1',
            children: []
        }]
    }]
};

我们用笔者画的d3 tree 看看是怎样的tree结构

https://codepen.io/AlexZ33/pe...

广度优先遍历：

function wideTraversal(node) {
    var nodes = [];
    if (node != null) {
        var queue = [];
        queue.unshift(node);
        while (queue.length != 0) {
            var item = queue.shift();
            nodes.push(item.name);
            var children = item.children;
            for (var i = 0; i < children.length; i++) {

                queue.push(children[i]);
            }
        }

    }
    return nodes;
}
console.log(wideTraversal(tree))

深度优先遍历：

function traverseTree(node) {
    var child = node.children,
        arr = [];

    arr.push(node.name);
    if (child) {
        child.forEach(function(node) {
            arr = arr.concat(traverseTree(node));
        });
    }
    return arr;
}
console.log(traverseTree(tree))

关系型数组转换成树形结构对象

var data = [
    { parentId: 0, id: 1, value: '1' },
    { parentId: 3, id: 2, value: '2' },
    { parentId: 0, id: 3, value: '3' },
    { parentId: 1, id: 4, value: '4' },
    { parentId: 1, id: 5, value: '5' }
]

期望输出:

[{"id":1,"value":"1","children":[{"id":4,"value":"4","children":[]},{"id":5,"value":"5","children":[]}]},{"id":3,"value":"3","children":[{"id":2,"value":"2","children":[]}]}]

var getJsonTree = function(data, parentId) {
    var itemArr = [];
    for (var i = 0; i < data.length; i++) {
        var node = data[i];
        //data.splice(i, 1)
        if (node.parentId == parentId) {
            var newNode = { id: node.id, value: node.value, children: getJsonTree(data, node.id) };
            itemArr.push(newNode);
        }
    }
    return itemArr;
}
console.log(getJsonTree(data, 0))

参考

Depth-first search
[数据结构与算法 javascript描述]
[慕课网 算法与数据结构]
数据结构和算法系列17
Graph (abstract data type))
Topological sorting
Topological Sorting
拓扑排序（Topological Sorting）
数据结构与算法 - 图论
Breadth-first search 广度优先搜索