红黑树的删除

红黑树的删除

可能出现的情形讨论

删除红黑树中一个结点，删除的结点是其子结点状态和颜色的组合。子结点的状态有三种：无子结点、只有一个子结点、有两个子结点。颜色有红色和黑色两种。所以共会有6种组合。

组合1：被删结点无子结点，且被删结点为红色

此时直接将结点删除即可，不破坏任何红黑树的性质。

组合2：被删结点无子结点，且被删结点为黑色

处理方法略微复杂，稍后再议。

组合3：被删结点有一个子结点，且被删结点为红色

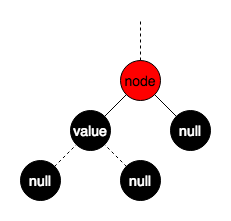
这种组合是不存在的，如图假如被删结点node只有一个有值的子结点value，而以value为根结点的子树中，必然还存在null结点，如此不符合红黑树的性质5，对每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。

组合4：被删结点有一个子结点，且被删结点为黑色

这种组合下，被删结点node的另一个子结点value必然为红色，此时直接将node删掉，用value代替node的位置，并将value着黑即可。

组合5&6：被删结点有两个子结点，且被删结点为黑色或红色

当被删结点node有两个子结点时，先要找到这个被删结点的后继结点successor，然后用successor代替node的位置，同时着成node的颜色，此时相当于successor被删。

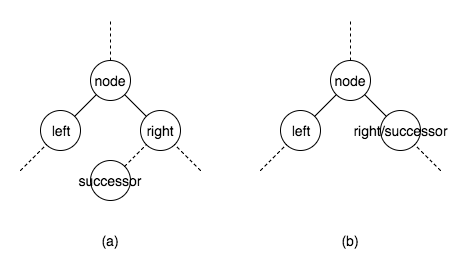
因为node有两个子结点，所以successor必然在node的右子树中，必然是下图两种形态中的一种。

若是(a)的情形，用successor代替node后，相当于successor被删，若successor为红色，则变成了组合1；若successor为黑色，则变成了组合2。

若是(b)的情形，用successor代替node后，相当于successor被删，若successor为红色，则变成了组合1；若successor为黑色，则变成了组合2或4。

综上

若被删结点是组合1或组合4的状态，很容易处理；被删结点不可能是组合3的状态；被删结点是组合5&6的状态，将变成组合1或组合2或组合4。

再议组合2：被删结点无子结点，且被删结点为黑色

因为删除黑色结点会破坏红黑树的性质5，所以为了不破坏性质5，在替代结点上额外增加一个黑色，这样不违背性质5而只违背性质1，每个结点或是黑色或是红色。此时将额外的黑色移除，则完成删除操作。

然后再结合node原来的父结点father和其兄弟结点brother来分析。

情形一

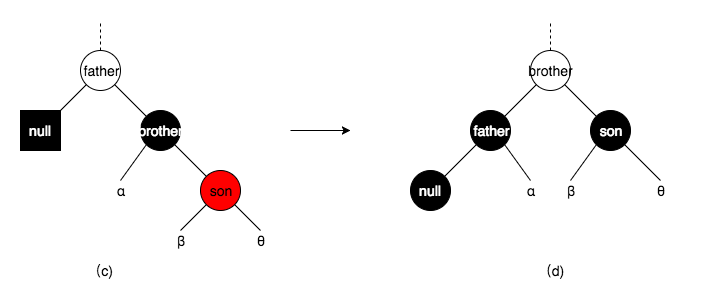
brother为黑色，且brother有一个与其方向一致的红色子结点son，所谓方向一致，是指brother为father的左子结点，son也为brother的左子结点；或者brother为father的右子结点，son也为brother的右子结点。

图(c)中，白色代表随便是黑或是红，方形结点除了存储自身黑色外，还额外存储一个黑色。将brother和father旋转，并重新上色后，变成了图(d)，方形结点额外存储的黑色转移到了father，且不违背任何红黑树的性质，删除操作完成。

图(c)中的情形颠倒过来，也是一样的操作。

情形二

brother为黑色，且brother有一个与其方向不一致的红色子结点son

图(e)中，将son和brother旋转，重新上色后，变成了图(f)，情形一。

图(e)中的情形颠倒过来，也是一样的操作。

情形三

brother为黑色，且brother无红色子结点

此时若father为红，则重新着色即可，删除操作完成。如图下图(g)和(h)。

此时若father为黑，则重新着色，将额外的黑色存到father，将father作为新的结点进行情形判断，遇到情形一、情形二，则进行相应的调整，完成删除操作；如果没有，则结点一直上移，直到根结点存储额外的黑色，此时将该额外的黑色移除，即完成了删除操作。

情形四

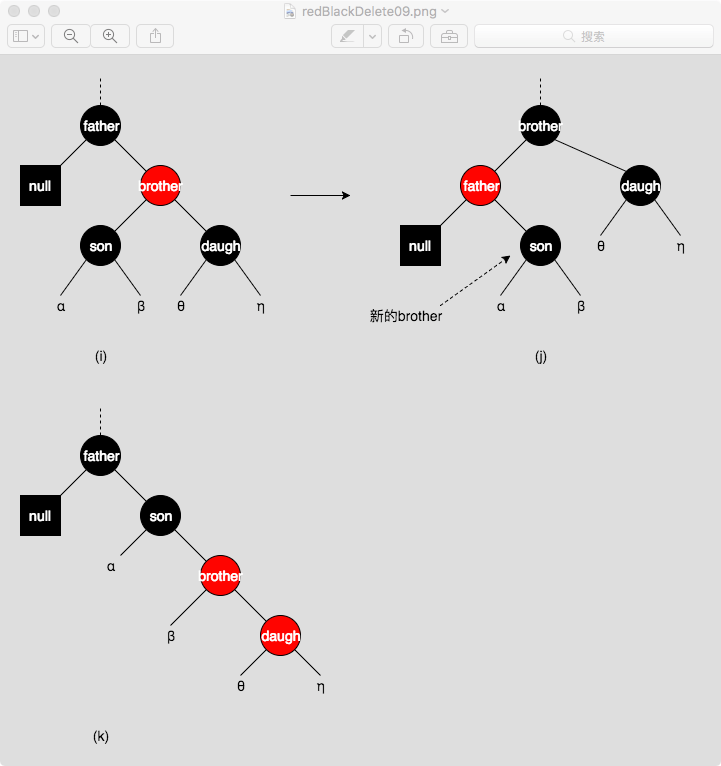
brother为红色，则father必为黑色。

图(i)中，将brother和father旋转，重新上色后，变成了图(j)，新的brother变成了黑色，这样就成了情形一、二、三中的一种。如果将son和brother旋转，无论怎么重新上色，都会破坏红黑树的性质4或5，例如图(k)。
图(i)中的情形颠倒过来，也是一样的操作。

代码

// 结点
function Node(value) {
  this.value = value
  this.color = 'red' // 结点的颜色默认为红色
  this.parent = null
  this.left = null
  this.right = null
}

function RedBlackTree() {
  this.root = null
}

RedBlackTree.prototype.insert = function (node) {
  // 以二叉搜索树的方式插入结点
  // 如果根结点不存在，则结点作为根结点
  // 如果结点的值小于node，且结点的右子结点不存在，跳出循环
  // 如果结点的值大于等于node，且结点的左子结点不存在，跳出循环
  if (!this.root) {
    this.root = node
  } else {
    let current = this.root
    while (current[node.value <= current.value ? 'left' : 'right']) {
      current = current[node.value <= current.value ? 'left' : 'right']
    }
    current[node.value <= current.value ? 'left' : 'right'] = node
    node.parent = current
  }
  // 判断情形
  this._fixTree(node)
  return this
}

RedBlackTree.prototype._fixTree = function (node) {
  // 当node.parent不存在时，即为情形1，跳出循环
  // 当node.parent.color === 'black'时，即为情形2，跳出循环
  while (node.parent && node.parent.color !== 'black') {
    // 情形3
    let father = node.parent
    let grand = father.parent
    let uncle = grand[grand.left === father ? 'right' : 'left']
    if (!uncle || uncle.color === 'black') {
      // 叶结点也是黑色的
      // 情形3.1
      let directionFromFatherToNode = father.left === node ? 'left' : 'right'
      let directionFromGrandToFather = grand.left === father ? 'left' : 'right'
      if (directionFromFatherToNode === directionFromGrandToFather) {
        // 具体情形一或二
        // 旋转
        this._rotate(father)
        // 变色
        father.color = 'black'
        grand.color = 'red'
      } else {
        // 具体情形三或四
        // 旋转
        this._rotate(node)
        this._rotate(node)
        // 变色
        node.color = 'black'
        grand.color = 'red'
      }
      break // 完成插入，跳出循环
    } else {
      // 情形3.2
      // 变色
      grand.color = 'red'
      father.color = 'black'
      uncle.color = 'black'
      // 将grand设为新的node
      node = grand
    }
  }

  if (!node.parent) {
    // 如果是情形1
    node.color = 'black'
    this.root = node
  }
}

RedBlackTree.prototype._rotate = function (node) {
  // 旋转 node 和 node.parent
  let y = node.parent
  if (y.right === node) {
    if (y.parent) {
      y.parent[y.parent.left === y ? 'left' : 'right'] = node
    }
    node.parent = y.parent
    if (node.left) {
      node.left.parent = y
    }
    y.right = node.left
    node.left = y
    y.parent = node
  } else {
    if (y.parent) {
      y.parent[y.parent.left === y ? 'left' : 'right'] = node
    }
    node.parent = y.parent
    if (node.right) {
      node.right.parent = y
    }
    y.left = node.right
    node.right = y
    y.parent = node
  }
}

RedBlackTree.prototype.remove = function (node) {
  while (true) {
    let {
      left,
      right,
      parent,
      color
    } = node
    // 组合1
    if (!left && !right && color === 'red') {
      parent[parent.left === node ? 'left' : 'right'] = null
      return this
    }
    // 组合2
    if (!left && !right && color === 'black') {
      if (parent) {
        let nullNode = new Node(null)
        nullNode.parent = parent
        nullNode.color = ['black', 'black']
        parent[parent.left === node ? 'left' : 'right'] = nullNode
        this._repairTree(nullNode)
      } else {
        this.root = null
      }
      return this
    }
    // 组合4
    if ((!left && right && color === 'black') || (left && !right && color === 'black')) {
      if (parent) {
        parent[parent.left === node ? 'left' : 'right'] = node.left || node.right
      } else {
        this.root = node.left || node.right
      }
      node[node.left ? 'left' : 'right'].color = 'black'
      return this
    }
    // 组合5&6
    if (left && right) {
      // 寻找后继结点
      let successor = right
      while (successor.left) {
        successor = successor.left
      }
      // 用后继结点代替node
      node.value = successor.value
      // 删除后街结点
      node = successor
      /* let successorColor = successor.color
      let successorLeft = successor.left
      let successorRight = successor.right
      let successorParent = successor.parent
      // 用后继节点代替node
      if (parent) {
        parent[parent.left === node ? 'left' : 'right'] = successor
      } else {
        this.root = successor
      }
      successor.parent = parent
      successor.left = left
      successor.right = right
      left.parent = successor
      right.parent = successor
      successor.color = color
      // 删除successor
      node.left = successorLeft
      node.right = successorRight
      node.parent = successorParent
      node.color = successorColor */
    }
  }
}

RedBlackTree.prototype._repairTree = function (node) {
  while (node.parent) {
    let father = node.parent
    let brother = father[father.left === node ? 'right' : 'left']
    let son = brother[father.left === node ? 'right' : 'left']
    let daugh = brother[father.left === node ? 'left' : 'right']
    if (brother.color === 'black') {
      if (son && son.color === 'red') {
        // 情形一
        // 旋转brother和father
        this._rotate(brother)
        // 变色
        brother.color = father.color
        father.color = 'black'
        son.color = 'black'
        // 移除black
        if (!node.value) {
          // nullNode
          father[father.left === node ? 'left' : 'right'] = null
        } else {
          node.color = 'black'
        }
        // 删除操作完成
        return
      } else if (daugh && daugh.color === 'red') {
        // 情形二
        // 旋转son和brother
        this._rotate(son)
        // 变色
        son.color = 'black'
        brother.color = 'red'
        // 变成情形一，继续循环
      } else {
        // 情形三
        // brother无红子结点
        if (father.color === 'red') {
          // father为红色
          father.color = 'black'
          brother.color = 'red'
          // 移除black
          if (!node.value) {
            // nullNode
            father[father.left === node ? 'left' : 'right'] = null
          } else {
            node.color = 'black'
          }
          // 删除操作完成
          return
        } else {
          // father为黑色
          father.color = ['black', 'black']
          brother.color = 'red'
          // 移除black
          if (!node.value) {
            // nullNode
            father[father.left === node ? 'left' : 'right'] = null
          } else {
            node.color = 'black'
          }
          node = father
          // 结点上移，继续循环
        }
      }
    } else {
      // 情形四
      this._rotate(brother)
      brother.color = 'black'
      father.color = 'red'
      // 继续循环
    }
  }
  this.root = node
  node.color = 'black'
}

RedBlackTree.prototype.find = function (value) {
  let current = this.root
  while (current.value !== value) {
    current = current[value >= current.value ? 'right' : 'left']
  }
  return current
}

let arr = [11, 2, 14, 1, 7, 15, 5, 8, 4]
let tree = new RedBlackTree()
arr.forEach(i => tree.insert(new Node(i)))
let findNode = tree.find(15)
tree.remove(findNode)
debugger

红黑树的插入

一点感悟

红黑树的插入和删除都是通过分类讨论来解决的，耐心的分析即可。
为数不多使用技巧的地方，是为了维持红黑树的性质，在结点上存两个黑色，当然这是算法导论告诉我的。