我的github博客地址 https://github.com/hujiulong/...
前言
在前端开发中,贝赛尔曲线无处不在:
- 它可以用来绘制曲线,在svg和canvas中,原生提供的曲线绘制都是使用贝赛尔曲线
- 它也可以用来描述一个缓动算法,设置css的
transition-timing-function属性,可以使用贝塞尔曲线来描述过渡的缓动计算 - 几乎所有前端2D或3D图形图表库(echarts,d3,three.js)都会使用到贝塞尔曲线
这篇文章我准备从实现一个非常简单的曲线动画效果入手,帮助大家彻底地弄懂什么是贝塞尔曲线,以及它有哪些特性,文章中有一点点数学公式,但是都非常简单:)。

可以点击这里查看在线演示
在写代码之前,先了解一下什么是贝塞尔曲线吧。
贝塞尔曲线
贝塞尔曲线(Bezier curve)是计算机图形学中相当重要的参数曲线,它通过一个方程来描述一条曲线,根据方程的最高阶数,又分为线性贝赛尔曲线,二次贝塞尔曲线、三次贝塞尔曲线和更高阶的贝塞尔曲线。
下面详细介绍一下用得比较多的二次贝塞尔曲线和三次贝塞尔曲线
二次贝塞尔曲线
二次贝塞尔曲线由三个点P0,P1,P2来确定,这些点也被称作控制点。曲线的方程为:
这个方程其实有它的几何意义,它表示可以通过这样的步骤来绘制一条曲线:
- 选定一个
0-1的t值 - 通过
P0和P1计算出点Q0,Q0在P0P1连成的直线上,并且length( P0, Q0 ) = length( P0, P1 ) * t - 同样,通过
P1和P2计算出Q1,使得length( P1, Q1 ) = length( P1, P2 ) * t - 再重复一次这个步骤,通过
Q1和Q2计算出B,使得length( Q0, Q1 ) = length( Q0, B ) * t。B就为当前曲线上的点
注:上面的length表示两点之间的长度

有了曲线方程,我们直接代入具体的t值就能算出点B了。
如果将t的值从0过渡到1,不断计算点B,就可以得到一条二次贝塞尔曲线:
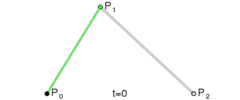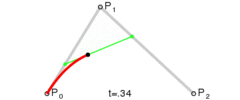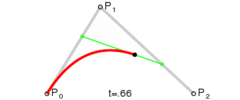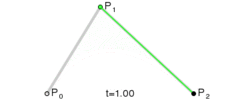
在canvas中,绘制二次贝塞尔曲线的方法为
ctx.quadraticCurveTo( p1x, p1y, p2x, p2y )其中p1x, p1y, p2x, p2y为后两个控制点(P1和P2)的横纵坐标,它默认将当前路径的起点作为一个控制点(P0)。
三次贝塞尔曲线
三次贝塞尔曲线需要四个点P0,P1,P2,P3来确定,曲线方程为
它的计算过程和二次贝塞尔曲线类似,这里不再赘述,可以看下图:

同样,将t的值从0过渡到1,就可以绘制出一条三次贝塞尔曲线:

在canvas中,绘制三次贝塞尔曲线的方法为
ctx.bezierCurveTo( p1x, p1y, p2x, p2y, p3x, p3y )其中p1x, p1y, p2x, p2y, p3x, p3y为后三个控制点(P1,P2和P3)的横纵坐标,它默认将当前路径的起点作为一个控制点(P0)。
贝塞尔曲线的特征
在三次贝塞尔曲线后面,还有更高阶的贝塞尔曲线,同样它们绘制的过程也更加复杂
四次贝塞尔曲线
图:四次贝塞尔曲线
五次贝塞尔曲线

我们可以归纳出贝塞尔曲线有几个重要的特征:
- n阶贝塞尔曲线需要n+1个点来确定
- 贝塞尔曲线是平滑的
- 贝塞尔曲线的起点和终点与对应控制点的连线相切
绘制贝塞尔曲线
复习完基础概念,接下来就要讲如果绘制贝塞尔曲线啦
为简单起见,我们选择使用二次贝塞尔曲线。
我们先不考虑动画的事,我们先将问题简化成:给定一个起点和一个终点,需要实现一个函数,它能够绘制出一条曲线。
也就是说我们需要实现一个函数drawCurvePath,除渲染上下文ctx外(不清楚ctx是什么的同学可以先熟悉下canvas的基本概念),它接受三个参数,分别为二次贝塞尔曲线的三个控制点。我们将样式控制移到函数外,drawCurvePath只用来绘制路径。
/**
* 绘制二次贝赛尔曲线路径
* @param {Object} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
// ...
}前文提到过,在canvas中,绘制二次贝赛尔曲线的方法是quadraticCurveTo,所以只要短短两行就能完成这个方法。
/**
* 绘制二次贝赛尔曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} p0
* @param {Array<number>} p1
* @param {Array<number>} p2
*/
function drawCurvePath( ctx, p0, p1, p2 ) {
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
p1[ 0 ], p1[ 1 ],
p2[ 0 ], p2[ 1 ]
);
}这样就完成了基本的绘制二次贝塞尔曲线的方法了。
但是函数这样设计有点小问题
如果我们是在做一个图形库,我们想给使用者提供一个绘制曲线的方法。
对于使用者来说,他只想在给定的起点和终点间间绘制一条曲线,他想要得到的曲线尽量美观,但是又不想关心具体的实现细节,如果还需要给第三个点,使用者会有一定的学习成本(至少需要弄明白什么是贝塞尔曲线)。
看到这里你可能会比较疑惑,即使是二次贝塞尔曲线也需要三个控制点,只有起点和终点怎么绘制曲线呢。
我们可以在起点和终点的垂直平分线上选一点作为第三个控制点,可以提供给使用者一个参数来控制曲线的弯曲程度,现在函数就变成了这样
/**
* 绘制一条曲线路径
* @param {CanvasRenderingContext2D} ctx
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}我们用curveness来表示曲线的弯曲程度,也就是第三个控制点的偏离程度。这样很容易就能计算出中间点。
现在完整的函数变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
*/
function drawCurvePath( ctx, start, end, curveness ) {
// 计算中间控制点
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
ctx.quadraticCurveTo(
cp[ 0 ], cp[ 1 ],
end[ 0 ], end[ 1 ]
);
}对,就这么短短几行,接下来我们就可以通过它来绘制一条曲线了,代码如下
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.4
);
ctx.stroke();
function drawCurvePath( ctx, start, end, curveness ) {
// ...
}
</script>
</body>
</html>绘制结果:
绘制一条曲线
绘制贝塞尔曲线动画
终于来到文章的本体啦,我们的目的不是绘制一条静态的曲线,我们想绘制一条有过渡效果的曲线。
简化一下问题,那就是我们希望绘制曲线的函数还接受另一个参数,表示绘制曲线的百分比。我们定时去调用这个函数,递增百分比这个参数,就能画出动画了。
我们新增一个参数percent来表示百分比,现在函数变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}但是canvas提供的quadraticCurveTo方法只能绘制一条完整的二次贝赛尔曲线,没有办法去控制它只画一部分。
画完后用clearRect擦除掉一部分?这不太可行,因为很难确定要擦除的范围。如果曲线的线宽比较宽,就还需要保证擦除的边界和曲线末端垂直,问题就变得很复杂了。
现在再重新看看这张图
我们是不是可以将percent这个参数理解成t值,然后通过贝赛尔曲线方程去计算出中间所有的点,用直线连接起来,以此模拟绘制贝赛尔曲线的一部分呢?
方法一
我们不再用canvas提供的quadraticCurveTo来绘制曲线,而是通过贝赛尔曲线的方程计算出一系列点,用多端直线来模拟曲线。
这样做的好处时,我们可以很容易的控制绘制的范围。
那么函数实现就变成了这样:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
ctx.moveTo( start[ 0 ], start[ 1 ] );
for ( var t = 0; t <= percent / 100; t += 0.01 ) {
var x = quadraticBezier( start[ 0 ], cp[ 0 ], end[ 0 ], t );
var y = quadraticBezier( start[ 1 ], cp[ 1 ], end[ 1 ], t );
ctx.lineTo( x, y );
}
}
function quadraticBezier( p0, p1, p2, t ) {
var k = 1 - t;
return k * k * p0 + 2 * ( 1 - t ) * t * p1 + t * t * p2; // 这个方程就是二次贝赛尔曲线方程
}接下来就可以通过设置定时器,每隔一段时间调用一次这个方法,并且递增percent
为了动画更加平滑,我们使用requestAnimationFrame来代替定时器
<!DOCTYPE html>
<html lang="en">
<head>
<title>draw curve</title>
</head>
<body>
<canvas id="canvas" width="800" height="800"></canvas>
<script>
var canvas = document.getElementById( 'canvas' );
var ctx = canvas.getContext( '2d' );
ctx.lineWidth = 2;
ctx.strokeStyle = '#000';
var percent = 0;
function animate() {
ctx.clearRect( 0, 0, 800, 800 );
ctx.beginPath();
drawCurvePath(
ctx,
[ 100, 100 ],
[ 200, 300 ],
0.2,
percent
);
ctx.stroke();
percent = ( percent + 1 ) % 100;
requestAnimationFrame( animate );
}
animate();
function drawCurvePath( ctx, start, end, curveness, percent ) {
// ...
}
</script>
</body>
</html>得到的结果:
这样基本实现了我们的需求,但它有一个问题:
测试发现,进行一次lineTo的时间和一次quadraticCurveTo的时间差不多,但是quadraticCurveTo只需要一次就能画出曲线,而使用lineTo则需要数十次。
换言之,用这样的方式绘制曲线,和我们前面的实现方式相比性能下降了数十倍之多。在绘制一条曲线时可能感觉不到区别,但是如果需要同时绘制上千条曲线,性能就会受到很大的影响。
方法二
那有没有什么方法可以做到用quadraticCurveTo来实现绘制完整曲线的一部分呢?
我们再次回到这张图
在中间的某一时刻,例如t=0.25时,它是这样的:
我们注意到,曲线P0-B这一段似乎也是贝赛尔曲线,它的控制点变成了P0,Q0,B。
现在问题就迎刃而解了,我们只需要每次计算出Q0,B,就能得到其中一小段贝赛尔曲线的控制点,然后就可以通过quadraticCurveTo来绘制它了。
代码如下:
/**
* 绘制一条曲线路径
* @param {Object} ctx canvas渲染上下文
* @param {Array<number>} start 起点
* @param {Array<number>} end 终点
* @param {number} curveness 曲度(0-1)
* @param {number} percent 绘制百分比(0-100)
*/
function drawCurvePath( ctx, start, end, curveness, percent ) {
var cp = [
( start[ 0 ] + end[ 0 ] ) / 2 - ( start[ 1 ] - end[ 1 ] ) * curveness,
( start[ 1 ] + end[ 1 ] ) / 2 - ( end[ 0 ] - start[ 0 ] ) * curveness
];
var t = percent / 100;
var p0 = start;
var p1 = cp;
var p2 = end;
var v01 = [ p1[ 0 ] - p0[ 0 ], p1[ 1 ] - p0[ 1 ] ]; // 向量<p0, p1>
var v12 = [ p2[ 0 ] - p1[ 0 ], p2[ 1 ] - p1[ 1 ] ]; // 向量<p1, p2>
var q0 = [ p0[ 0 ] + v01[ 0 ] * t, p0[ 1 ] + v01[ 1 ] * t ];
var q1 = [ p1[ 0 ] + v12[ 0 ] * t, p1[ 1 ] + v12[ 1 ] * t ];
var v = [ q1[ 0 ] - q0[ 0 ], q1[ 1 ] - q0[ 1 ] ]; // 向量<q0, q1>
var b = [ q0[ 0 ] + v[ 0 ] * t, q0[ 1 ] + v[ 1 ] * t ];
ctx.moveTo( p0[ 0 ], p0[ 1 ] );
ctx.quadraticCurveTo(
q0[ 0 ], q0[ 1 ],
b[ 0 ], b[ 1 ]
);
}将前面写的页面替换成上面的代码,可以看到得到的结果是一样的:
绘制动画
现在已经解决了最关键的问题,我们可以绘制动画啦。
不过这一部分并不重要,我就不贴代码了。
完整代码可以看这里
结束
我的博客地址: https://github.com/hujiulong/...
我会在这里分享我的学习成果和经验,特别是canvas/WebGL/svg这方面的技术。如果有对前端图形绘制感兴趣的同学可以关注一下我的博客,收藏点star,订阅点watch。
最近才将博客搬到github,所以文章并不多,我会坚持写下去的!








**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。