只进行基本的四则运算,利用栈结构和后缀表达式来计算数学表达式的值。
本文代码:GitHub 原文:wuyin.io 转载请注明来源。
运行效果:
问题
如果只能进行两个值的加减乘除,如何编程计算一个数学表达式的值?
比如计算 1+2*3+(4*5+6)*7,我们知道优先级顺序 () 大于 * / 大于 + - ,直接计算得 1+6+26*7 = 189
中缀、后缀表达式的计算
人利用中缀表达式计算值
数学表达式的记法分为前缀、中缀和后缀记法,其中中缀就是上边的算术记法: 1+2*3+(4*5+6)*7,人计算中缀表达式的值:把表达式分为三部分1 2+3 (4*5+6)*7 分别计算值,求和得 189。但这个理解过程在计算机上的实现就复杂了。
计算机利用后缀表达式计算值
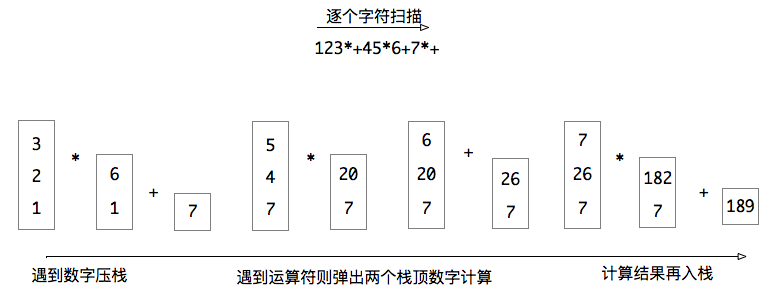
中缀表达式 1+2*3+(4*5+6)*7 对应的后缀表达式: 123*+45*6+7*+,计算机使用栈计算后缀表达式值:
计算后缀表达式的代码实现
func calculate(postfix string) int {
stack := stack.ItemStack{}
fixLen := len(postfix)
for i := 0; i < fixLen; i++ {
nextChar := string(postfix[i])
// 数字:直接压栈
if unicode.IsDigit(rune(postfix[i])) {
stack.Push(nextChar)
} else {
// 操作符:取出两个数字计算值,再将结果压栈
num1, _ := strconv.Atoi(stack.Pop())
num2, _ := strconv.Atoi(stack.Pop())
switch nextChar {
case "+":
stack.Push(strconv.Itoa(num1 + num2))
case "-":
stack.Push(strconv.Itoa(num1 - num2))
case "*":
stack.Push(strconv.Itoa(num1 * num2))
case "/":
stack.Push(strconv.Itoa(num1 / num2))
}
}
}
result, _ := strconv.Atoi(stack.Top())
return result
}现在只需知道如何将中缀转为后缀,再利用栈计算即可。
中缀表达式转后缀表达式
转换过程
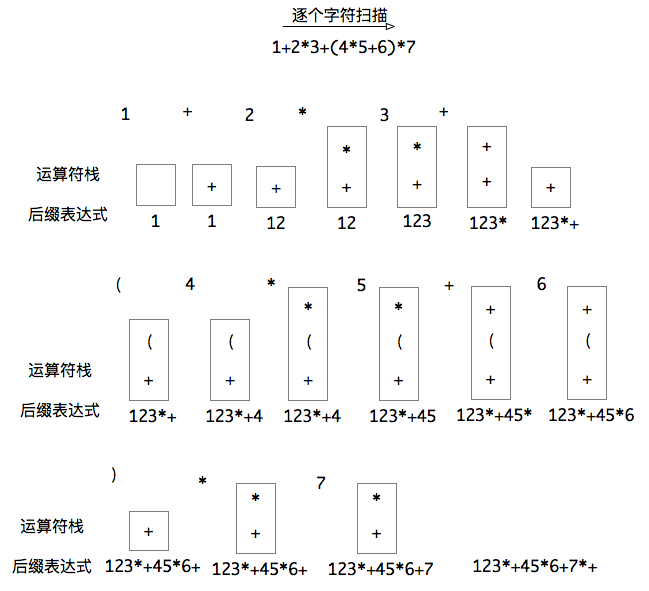
从左到右逐个字符遍历中缀表达式,输出的字符序列即是后缀表达式:
- 遇到数字直接输出
-
遇到运算符则判断:
- 栈顶运算符优先级更低则入栈,更高或相等则直接输出
- 栈为空、栈顶是
(直接入栈 - 运算符是
)则将栈顶运算符全部弹出,直到遇见)
- 中缀表达式遍历完毕,运算符栈不为空则全部弹出,依次追加到输出
转换的代码实现
// 中缀表达式转后缀表达式
func infix2ToPostfix(exp string) string {
stack := stack.ItemStack{}
postfix := ""
expLen := len(exp)
// 遍历整个表达式
for i := 0; i < expLen; i++ {
char := string(exp[i])
switch char {
case " ":
continue
case "(":
// 左括号直接入栈
stack.Push("(")
case ")":
// 右括号则弹出元素直到遇到左括号
for !stack.IsEmpty() {
preChar := stack.Top()
if preChar == "(" {
stack.Pop() // 弹出 "("
break
}
postfix += preChar
stack.Pop()
}
// 数字则直接输出
case "0", "1", "2", "3", "4", "5", "6", "7", "8", "9":
j := i
digit := ""
for ; j < expLen && unicode.IsDigit(rune(exp[j])); j++ {
digit += string(exp[j])
}
postfix += digit
i = j - 1 // i 向前跨越一个整数,由于执行了一步多余的 j++,需要减 1
default:
// 操作符:遇到高优先级的运算符,不断弹出,直到遇见更低优先级运算符
for !stack.IsEmpty() {
top := stack.Top()
if top == "(" || isLower(top, char) {
break
}
postfix += top
stack.Pop()
}
// 低优先级的运算符入栈
stack.Push(char)
}
}
// 栈不空则全部输出
for !stack.IsEmpty() {
postfix += stack.Pop()
}
return postfix
}
// 比较运算符栈栈顶 top 和新运算符 newTop 的优先级高低
func isLower(top string, newTop string) bool {
// 注意 a + b + c 的后缀表达式是 ab + c +,不是 abc + +
switch top {
case "+", "-":
if newTop == "*" || newTop == "/" {
return true
}
case "(":
return true
}
return false
}总结
计算机计算数学表达式的值分成了 2 步,利用 stack 将人理解的中缀表达式转为计算机理解的后缀表达式,再次利用 stack 计算后缀表达式的值。

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。