一.常见的排序算法及时间复杂度
二.各排序算法的理解及实现
1.冒泡排序(Bubble Sort)O(n²)
(1)算法描述
- 比较相邻元素,如果第一个比第二个大,交换位置,这样每经过一趟就冒出一个最大的
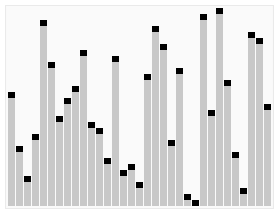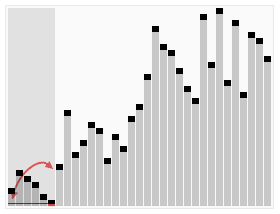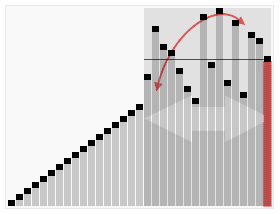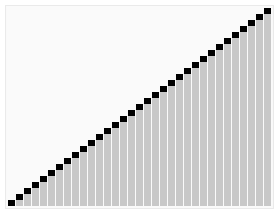
(2)动图演示
(3)代码实现
public static int[] bubbleSort(int arr[]){
int len = arr.length;
for(int i = 0;i<len;i++){
for(int j = 0;j<len-i-1;j++){
if(arr[j]>arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}2.快速排序 O(nlog2n)
(1)算法描述
- 从数列中挑出一个元素,称为"基准"(pivot)
- 从左向右找比这个第一个比这个基准大的数,从右往左找第一个比这个基准小的数,找到后互换位置
- 继续在此基础上执行第二步,直到两个寻找指针相遇
- 递归的(recursive)把小于基准值的序列和大于基准值的序列排序
(2)动图演示
public static void quickSort(int[]arr, int left,int right) {
if(left>right){return; }//递归的出口
int i = left,j = right;
int pivot = arr[left];//找到基准
while (i < j) {
//从右向左找第一个比基准值小的数
while (i < j && arr[j] >= pivot) {
j--;
}
//从左向右找第一个比基准值大的数
while (i < j && arr[i] <= pivot) {
i++;
}
//两面都找到后互换位置
if (i < j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
//left=right时于基准值互换
int tmp = arr[j];
arr[j] = arr[left];
arr[left] = tmp;
//分别递归的调用基准值的左边和右边
quickSort(arr,left,i-1);
quickSort(arr,i+1,right);
}
3.简单插入排序 O(n²)
(1)算法描述
- 从第二个元素开始(因为认为第一个元素已经有序)向前扫描
- 如果前一个数小于当前元素,继续跳到下一个元素开始向前扫描
- 如果前一个数大于当前元素,继续向前扫描,直到找到小于这个数的元素,插到它的后面
(2)动图演示
(3)代码实现
public static void insertSort(int[] array){
int len = array.length;
for(int i = 1;i<len;i++){
int temp = array[i];//待插入的数
int j;
//向前找比待插入数小的数
for(j = i;j>0 && array[j-1]>temp;j--){
//如果比待插入数大 ,向右移
array[j] = array[j-1];
}
//如果比带插入数小,插在该数后面
array[j] = temp;
}4.希尔排序 O(nlogn)
(1)算法描述
其实就是对插入排序进行了优化,先对相同间隔的一组数进行插入排序,使序列基本有序,再进行间隔为1的插入排序时,减少工作量。(代码实现可对照插入排序,其实就是多了一组循环)
(2)动图演示
(3)代码实现
public static void shellSort(int[] array){
int len= array.length;
int gap;//增量长度
for(gap = len/2;gap>0;gap/=2){
for(int i = gap;i<len;i++) {
//待插入的数
int temp = array[i];
int j;
//向前找比待插入数小的数,间隔为gap
for (j = i; j > gap && array[j - gap] > temp; j-=gap) {
//如果比待插入数大 ,向右移
array[j] = array[j - gap];
}
//如果比待插入数小,插在该数后面
array[j] = temp;
}
}
}5.简单选择排序 O(n²)
(1)算法描述
- 将序列划分为有序区和无序区(初始状态有序区为空)
- 遍历无序区,选出最小的元素,放到有序区
(2)动图演示
(3)代码实现
public static int[] selectSort(int array[]){
for(int i=0;i<array.length-1;i++){
int k = i;//k可以理解为目前无序区中的最小索引
for (int j = i+1;j<array.length;j++){
if(array[j]<array[k])
k = j;
}
//把无序区的最小值放到有序区末尾
int temp = array[i];
array[i] = array[k];
array[k] = temp;
}
return array;
}6.堆排序
(1)算法描述


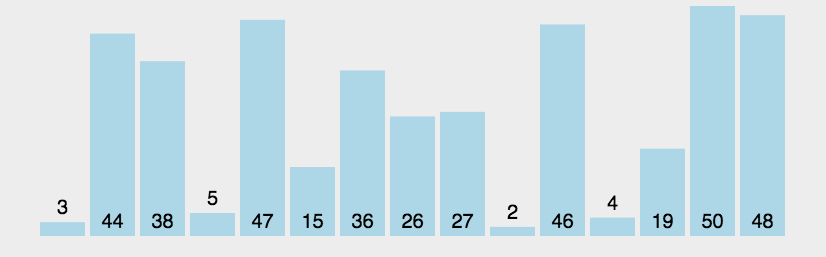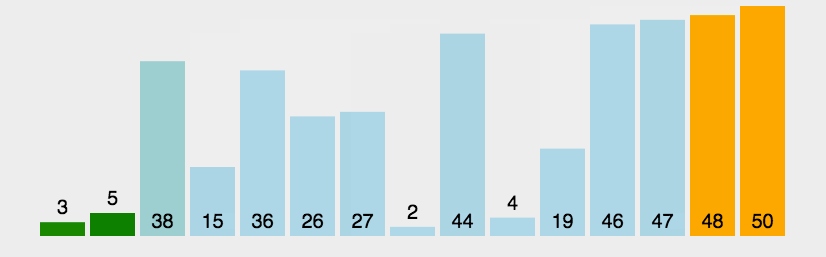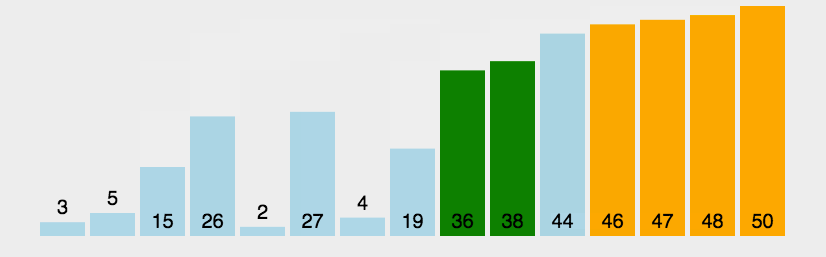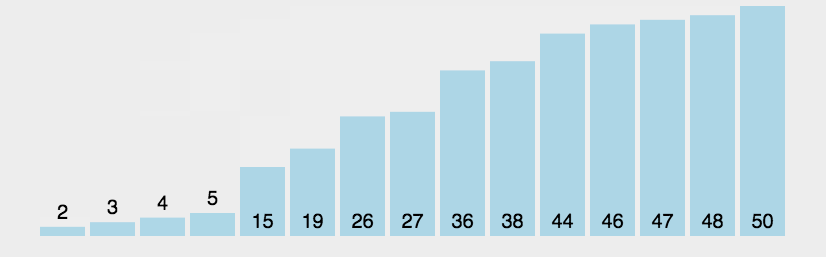



**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。