算法——指定日期的星期推算

  最近闲来无事，突然想了解下中国农历与中国阳历之间的关系，经过一番调研发现这里面的水还比较深，涉及天文学、历史、宗教等一些知识，发现挺有意思的就准备做一系列的总结，主要是防止自己忘记了，而且搜索了一下简书上的文章也么没有相关文章进行描述，所以借此机会跟大家分享同大家讨论，这篇文章是这个系列的第一篇，主要讲是如何推算指定日期的星期问题

根据已知日期进行推算

该方法主要是通过计算已知日期和指定日期之间的天数来推算，因为星期是一个非常固定的时间周期，7天一循环，因此通过计算出相差天数后，再对7进行取余操作就能推算出指定的日期的星期

根据公历平闰年计算

最常见的计算两个日期之间的天数就是根据年数进行推算，但是由于有闰年的影像，因此需要考虑闰年的情况，闰年的判断规则如下：

1. 公历年数是4的倍数，且不是100倍数
2. 公历年数是400倍数

满足上述两个条件中的一个既是闰年，该描述可以参考李永乐老师的视频讲解：闰年是怎么回事

依次遍历年份计算天数

经过分析我们发现两个日期之间的天数可分为三部分:

• 起始日期所在年中剩余的天数
• 结束日期所在年中已经度过的天数
• 中间年份的整年的天数

实现代码一

上述是一个通用描述，对于起止时间正好在一个年的开始和结尾，该方案也能描述。
因为中间是一个有可能存在闰年的，所需要根据闰年规则对每个年份进行判断，代码如下：

/**
     * @param startYear 起始年份
     * @param endYear 截止年份
     * @return 从起止年份到截止年份前一年的天数
     * 常量 YearDays.LEAP_YEAR_DAYS = 366
     * 常量 YearDays.NONLEAP_YEAR_DAYS = 365
     * @throws CalendarException
     */
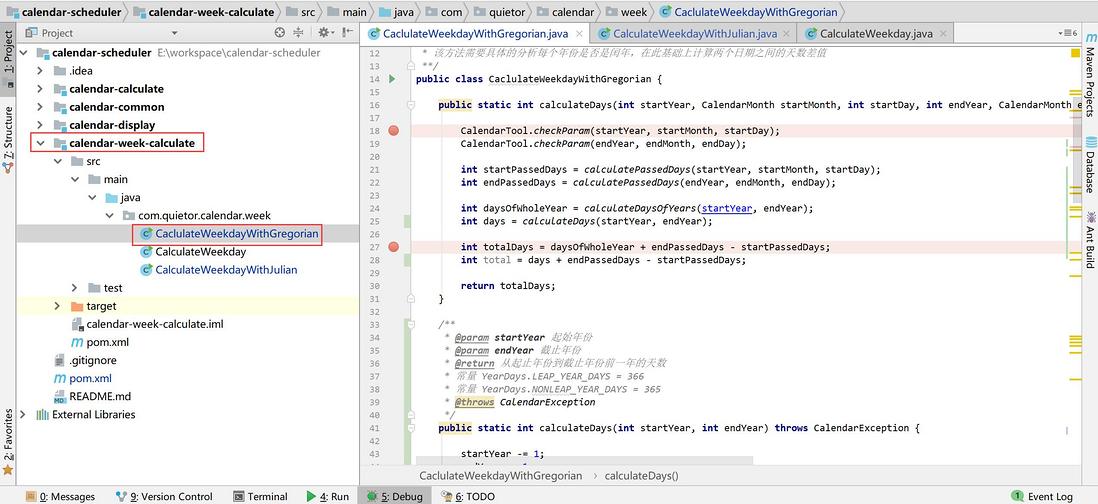
public static int calculateDaysOfYears(int startYear, int endYear) throws CalendarException {
        if(startYear > endYear) {
            throw new CalendarException(String.format("illegal parameter year, startYear=%s endYear=%s", startYear, endYear));
        }

        int difference = endYear - startYear;

        int totalDays = 0;
        //从起始年的1月1号开始加和，一直到截止年的前一年所有的天数，这样的计算需要减去起始年已经过过去的天数
        for(int i= startYear; i < endYear; i++) {
            boolean isLeap = CalendarTool.isLeapyear(i);
            if (isLeap) {
                totalDays += YearDays.LEAP_YEAR_DAYS;
            } else {
                totalDays += YearDays.NONLEAP_YEAR_DAYS;
            }
        }

        return totalDays;
    }

因为需要计算截止年月已经度过的天数，所以我复用了这个计算逻辑，以为剩余的天数 = 年内总天数 - 已经过的天数基于这个公式就能算出其实年份剩余的天数

 /**
     * 计算一年中到指定日期时已经度过的天数
     * @param year 年
     * @param month 枚举类型，定义了sort月数和 days天数两个属性
     * @param day 所在月的日期
     * @return
     */
    public static int calculatePassedDays(int year, CalendarMonth month, int day) throws CalendarException {
        CalendarTool.checkParam(year, month, day);

        int monthValue = month.getSort();

        int passedTotal = 0;
        for(int i = 1; i < monthValue; i++) {
            CalendarMonth passedMonth = CalendarMonth.getMonthBySort(i);
            if(passedMonth.equals(CalendarMonth.FEBRUARY)) {
                boolean isLeap = CalendarTool.isLeapyear(year);
                if(isLeap) {
                    passedTotal += 29;
                    continue;
                }
            }
            passedTotal += passedMonth.getDays();
        }

        return passedTotal + day;
    }

举个例子验证一下：已知1977年3月27日是星期天，计算2005年5月31日是星期几，按照上述的算法进行计算得到天数是10292，然后用10292 % 7 = 2得到余数为2，那么2005年5月31日就是星期二。

实现代码二

上述方法需要依次遍历起止年份之间的所有年份进行平闰年的判断，比较复杂，判断起来比较麻烦，其实我们只需要知道两个年份之间的闰年个数就可以解决我们的问题了，闰年的个数的计算公式：(分数结构部分表示向下取整)
$$ leap = \left\lfloor\frac y4\right\rfloor - \left\lfloor\frac y{100}\right\rfloor + \left\lfloor\frac y{400}\right\rfloor$$

• 公式中的y表示的当前年份，该公式结果是从公元元年到y年中所有闰年的个数，如果y年是闰年的话，y年也算在内。
• 这个公式中临界值确定需要注意，就是在起止年份，如果起止年份是闰年的话，要看起止年份是过了2月，这个直接关系到是+1天还是不加1天的问题。

这样就不需要遍历每个年份是否为闰年了，而直接计算天数即可，只需要将之前小节中计算整年天数代码进行调整，如下：

 /**
     * @param startYear 起始年份
     * @param endYear 截止年份
     * @return 从起止年份到截止年份前一年的天数
     * 常量 YearDays.LEAP_YEAR_DAYS = 366
     * 常量 YearDays.NONLEAP_YEAR_DAYS = 365
     * @throws CalendarException
     */
    public static int calculateDays(int startYear, int endYear) throws CalendarException {

        startYear -= 1;
        endYear -= 1;
        int startLeaps = Integer.valueOf(startYear / 4) - Integer.valueOf(startYear / 100) + Integer.valueOf(startYear / 400);
        int endLeaps = Integer.valueOf(endYear / 4) - Integer.valueOf(endYear / 100) + Integer.valueOf(endYear / 400);

        int totalDays = endLeaps * YearDays.LEAP_YEAR_DAYS + (endYear - endLeaps) * YearDays.NONLEAP_YEAR_DAYS -(startLeaps * YearDays.LEAP_YEAR_DAYS + (startYear - startLeaps) * YearDays.NONLEAP_YEAR_DAYS);

        return totalDays;
    }

年数-1是因为起止年份并不是完整年，计算之前的一年就不用考虑起止年份是否为闰年和月份是否过了2月份了，简化了逻辑判断。这样代码比之前的方法看起来精简了不少。

代码出处

上述代码片段可能不能满足大家的需要，所以附上代码出处

根据儒略日进行推算

上面的方法是根据平闰年进行推算的，需要进行复杂的平闰年判断，就算第二种方法也是简化了起止年份之间的年份的闰年判断，开始和结束年份的闰年判断再计算度过了多少天的时候还是要进行判断的，通过儒略日可以规避平闰年的判断。

儒略日

儒略日是一种不记年，不记月，只记日的历法，是由法国学者Joseph Justus Scaliger（1540－1609）在1583年提出来的一种以天数为计量单位的流水日历。儒略日就是指从公元前4713年1月1日UTC 12:00开始所经过的天数，JD0就被指定为公元前4713年1月1日 12:00到公元前4713年1月2日12:00之间的24小时，依次顺推，每一天都被赋予一个唯一的数字。使用儒略日可以把不同历法的年表统一起来，很方便地在各种历法中追溯日期。如果计算两个日期之间的天数，利用儒略日计算也很方便，先计算出两个日期的儒略日数，然后直接相减就可以得到两个日期相隔的天数。

儒略日公式

$$ julian = \left\lfloor 1461 \times \frac{y + 4716}{4} \right\rfloor + \left\lfloor 153 \times \frac{m + 1}{4}\right\rfloor + d + c - 1524.5 $$
y表示年份
m表示月份，如果m≤2则m修正为m+12，同时y修正为y-1
d表示日期
c的求值公式
$$ c = 2 - \left\lfloor\frac{y}{100} \right\rfloor + \left\lfloor\frac{y}{400}\right\rfloor $$

实现代码

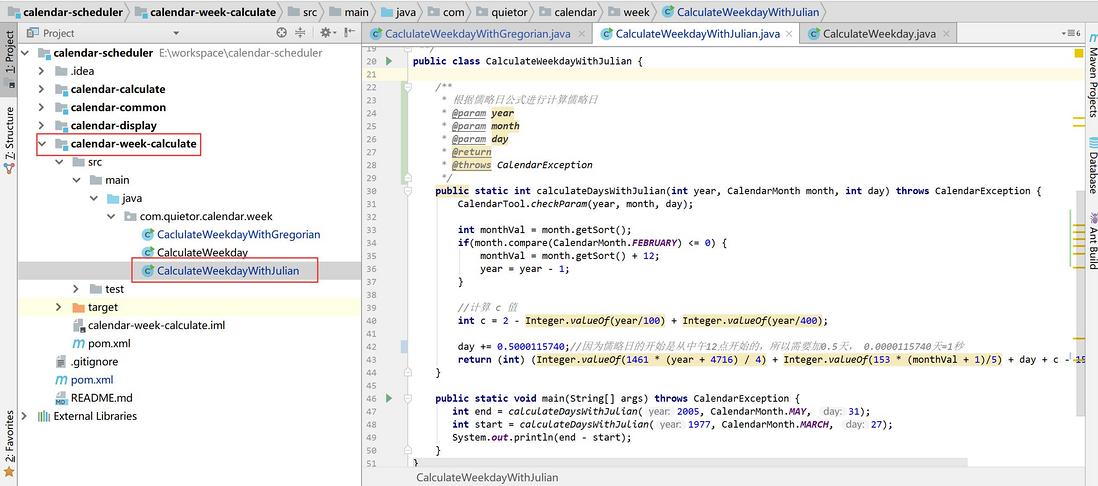
public static int calculateDaysWithJulian(int year, CalendarMonth month, int day) throws CalendarException {
        CalendarTool.checkParam(year, month, day);

        int monthVal = month.getSort();
        if(month.compare(CalendarMonth.FEBRUARY) <= 0) {
            monthVal = month.getSort() + 12;
            year = year - 1;
        }

        //计算 c 值
        int c = 2 - Integer.valueOf(year/100) + Integer.valueOf(year/400);

        //因为儒略日的开始是从中午12点开始的，所以需要加0.5天， 0.0000115740天=1秒
        day += 0.5000115740;
        return (int) (Integer.valueOf(1461 * (year + 4716) / 4) + Integer.valueOf(153 * (monthVal + 1)/5) + day + c - 1514.5);
    }

这样通过儒略日公式进行推算，代码较之前代码更加精简

代码出处

儒略日计算代码出处

直接定位日期所在星期

前面所述的推送方法都是基于已知日期的星期，然后计算与所指定的日期之间的天数来进行推算，在已知日期之后向后推算，在已知日期之前的向前推算，不是很方便。基于公元元年1月1日为周一，那么前一天就是下面介绍一个直接定位日期所在星期日，基于这个想法退出下面的公式。

计算公式

$$ weekday = ( y + \left\lfloor\frac{y}{4} \right\rfloor + \left\lfloor\frac{c}{4}\right\rfloor -2c + \left\lfloor\ 13 \times frac{m+1}{5} \right\rfloor + d - 1 ) \% 7 $$
上述公式适用1582年10月15日及之后的日期，对于1582年10月4及之前的公式：
$$ weekday = ( y + \left\lfloor\frac{y}{4} \right\rfloor + \left\lfloor\frac{c}{4}\right\rfloor -2c + \left\lfloor\ 13 \times frac{m+1}{5} \right\rfloor + d + 3 ) \% 7 $$

实现代码

/***
     * 计算指定日其所在的星期
     * 兼容1582年前后10月4日之前和1582年10月15之后的所有时间
     * @param year
     * @param month
     * @param day
     * @return
     * @throws CalendarException
     */
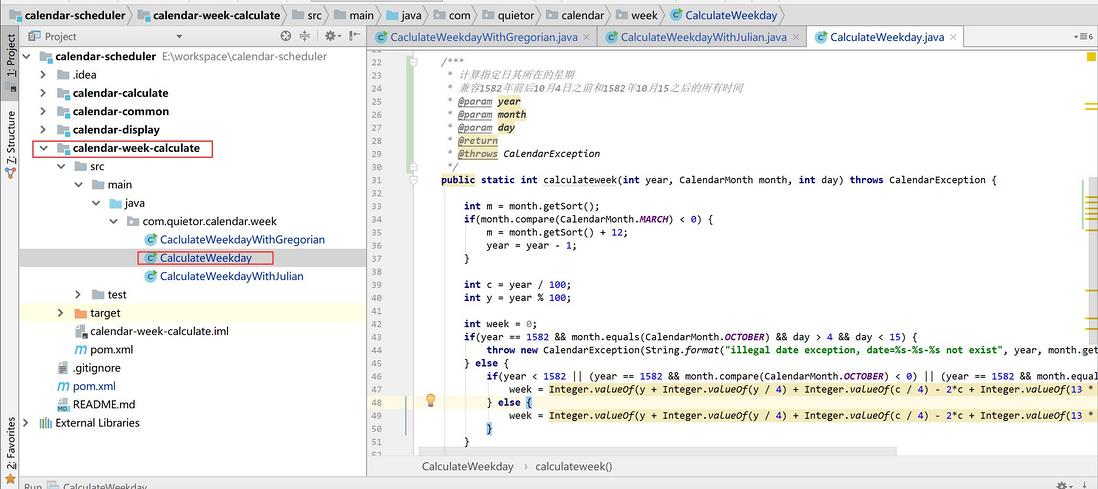
    public static int calculateweek(int year, CalendarMonth month, int day) throws CalendarException {

        int m = month.getSort();
        if(month.compare(CalendarMonth.MARCH) < 0) {
            m = month.getSort() + 12;
            year = year - 1;
        }

        int c = year / 100;
        int y = year % 100;

        int week = 0;
        if(year == 1582 && month.equals(CalendarMonth.OCTOBER) && day > 4 && day < 15) {
            throw new CalendarException(String.format("illegal date exception, date=%s-%s-%s not exist", year, month.getSort(), day));
        } else {
            if(year < 1582 || (year == 1582 && month.compare(CalendarMonth.OCTOBER) < 0) || (year == 1582 && month.equals(CalendarMonth.OCTOBER) && day <= 4)) {
                week = Integer.valueOf(y + Integer.valueOf(y / 4) + Integer.valueOf(c / 4) - 2*c + Integer.valueOf(13 * (m + 1) / 5) + day + 3) % 7;
            } else {
                week = Integer.valueOf(y + Integer.valueOf(y / 4) + Integer.valueOf(c / 4) - 2*c + Integer.valueOf(13 * (m + 1) / 5) + day - 1) % 7;
            }
        }

        // 公式会产生负数，修正即可
        if(week < 0)
            week = (week + 7) % 7;

        return week;

    }

代码出处

儒略日定位计算代码出处

这篇文章主要是从网上搜集来的知识并不是自己读书的来，以下是主要文档的出处
相关文档：
https://blog.csdn.net/orbit/a...
https://blog.csdn.net/orbit/a...
http://www.365yg.com/i6550819...