深入理解HashMap(一): 从源头说起

前言

系列文章目录

HashMap我们都不陌生, 也是java面试几乎必问的考点, 本系列我们来深入思考有关HashMap的设计思想和实现细节.

HashMap解决了什么问题?

任何数据结构的产生总对应着要解决一个实际的问题, HashMap的产生要解决问题就是:

如何有效的 存 取 一组 key-vaule 键值对

key-value键值对是最常使用的数据形式, 如何有效地存取他们是众多语言都需要关注的问题. 注意这里有四个关键字:

1. key-value键值对
2. 一组
3. 存
4. 取

下面我们逐个来思考:

如何表示 key-value 键值对

在java这种面向对象的语言中, 表示一个数据结构自然要用到类, 由于对于键值对的数据类型事先并不清楚, 显而易见这里应该要用泛型, 则, 表示key-value键值对最简单的形式可以是:

class Node<K,V> {
    K key;
    V value;
}

这里我们自定义一个Node类, 它只有两个属性, 一个 key属性表示键, 一个value属性表示值, 则这个类就代表了一个 key-value键值对.

是不是很简单?

当然, 我们还需要定义一些方法来操纵这两个属性, 例如get和set方法等,不过根据设计原则, 我们应该面向接口编程, 所以应该定义一个接口来描述需要执行的操作, 这个接口就是Entry<K,V>, 它只不过是对于Node<K,V>这个类的抽象, 在java中, 这个接口定义在Map这个接口中, 所以上面的类可以改为:

class Node<K,V> implements Map.Entry<K,V>{
    K key;
    V value;
}

这里我们总结一下:

我们定义了一个Node类来表示一个键值对, 为了面向接口编程, 我们抽象出一个 Entry接口, 并使Node类实现了这个接口.

至于这个接口需要定义哪些方法, 我们暂不细表.

这样, 到目前为止, 我们完成了对于 key-value 键值对的表示.

如何存储 key-value 键值对的集合

在常见的业务逻辑中, 我们常常需要处理一组键值对的集合, 将一组键值对存储在一处, 并根据key值去查找对应的value.

那么我们要如何存储这些键值对的集合呢?

其实换个问法可能更容易回答:

应该怎样存储一组对象?

(毕竟键值对已经被我们表示为Node对象了)

在java中, 存储一个对象的集合无外乎两种方式:

1. 数组
2. 链表

关于数组和链表的优缺点大家已经耳熟能详了:

• 数组大小有限, 查找性能好, 插入和删除性能差
• 链表大小不限, 查找性能差, 插入和删除性能好

这里应该选哪种形式呢? 那得看实际的应用了, 在使用键值对时, 查找和插入,删除等操作都会用到, 但是在实际的应用场景中, 对于键值对的查找操作居多, 所以我们当然选择数组形式.

Node<K,V>[] table;

总结: 我们选择数组形式来存储key-value对象.

为了便于下文描述, 我们将数组的下标称为索引(index), 将数组中的一个存储位置称为数组的一个存储桶(bucket).

如何有效地根据key值查找value

前面已经讲到, 我们选择数组形式来存储key-value对象, 以利用其优良的查找性能, 数组之所以查找迅速, 是因为可以根据索引(数组下标)直接定位到对应的存储桶(数组所存储对象的位置.)
但是实际应用中, 我们都是通过key值来查找value值, 怎么办呢?

一种方式就是遍历数组中的每一个对象, 查看它的key是不是我们要找的key, 但是很明显, 这种方式效率低下(而且这不就是链表的顺序查找方式吗?) 完全违背了我们选择数组来存储键值对的初衷.

为了利用索引来查找, 我们需要建立一个 key -> index 的映射关系, 这样每次我们要查找一个 key时, 首先根据映射关系, 计算出对应的数组下标, 然后根据数组下标, 直接找到对应的key-value对象, 这样基本能以o(1)的时间复杂度得到结果.

这里, 将key映射成index的方法称为hash算法, 我们希望它能将 key均匀的分布到数组中.

这里插一句,使用Hash算法同样补足了数组插入和删除性能差的短板, 我们知道, 数组之所以插入删除性能差是因为它是顺序存储的, 在一个位置插入节点或者删除节点需要一个个移动它的后续节点来腾出位或者覆盖位置.

使用hash算法后, 数组不再按顺序存储, 插入删除操作只需要关注一个存储桶即可, 而不需要额外的操作.

如何解决hash冲突

这个问题其实是由上一个问题引出的, 虽然我们要求hash算法能将key均匀的分布到数组中, 但是它只能尽量做到, 并不是绝对的, 更何况我们的数组大小是有限的, 保不齐我们的hash算法将就两个不同的key映射成了同一个index值, 这就产生了hash冲突, 也就是两个Node要存储在数组的同一个位置该怎么办?

解决hash冲突的方法有很多, 在HashMap中我们选择链地址法, 即在产生冲突的存储桶中改为单链表存储.(拓展阅读: 解决哈希冲突的常用方法 )

其实, 最理想的效果是，Entry数组中每个位置都只有一个元素，这样，查询的时候效率最高，不需要遍历单链表，也不需要通过equals去比较Key，而且空间利用率最大。

链地址法使我们的数组转变成了链表的数组:

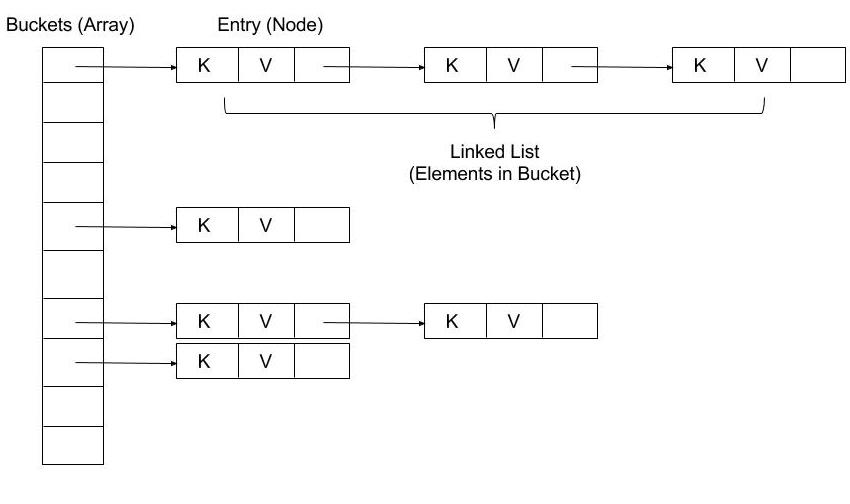
(图片来自网络)

至此, 我们对key-value键值对的表示变为:

class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
    
    Node(int hash, K key, V value, Node<K,V> next) {
        this.hash = hash;
        this.key = key;
        this.value = value;
        this.next = next;
    }
    ...
}

链表长度过长怎么办

我们知道, 链表查找只能通过顺序查找来实现, 因此, 时间复杂度为o(n), 如果很不巧, 我们的key值被Hash算法映射到一个存储桶上, 将会导致存储桶上的链表长度越来越长, 此时, 数组查找退化成链表查找, 则时间复杂度由原来的o(1) 退化成 o(n).

为了解决这一问题, 在java8中, 当链表长度超过 8 之后, 将会自动将链表转换成红黑树, 以实现 o(log n) 的时间复杂度, 从而提升查找性能.

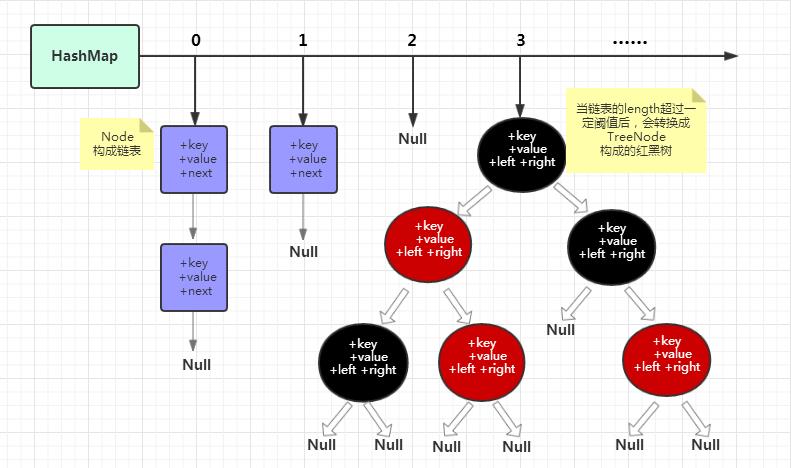
(图片来自网络)

什么时候扩容

前面已经说到, 数组的大小是有限的, 在新建的时候就要指定, 如果加入的节点已经到了数组容量的上限, 已经没有位置能够存储key-value键值对了, 此时就需要扩容.

但是很明显, 我们不会等到火烧眉毛了才想起来要扩容, 在实际的应用中, 数组空间已使用3/4之后, 我们就会括容.

为什么是0.75呢, 官方文档的解释是:

the default load factor (.75) offers a good tradeoff between time and space costs.

想要更深入的理解可以看这里.

再说回扩容, 有的同学就要问了, 咱上面不是将数组的每一个元素转变成链表了吗? 就算此时节点数超过了数组大小, 新加的节点会存在数组某一个位置的链表里啊, 链表的大小不限, 可以存储任意数量的节点啊!

没错, 理论上来说这样确实是可行的, 但这又违背了我们一开始使用数组来存储一组键值对的初衷, 还记得我们选择数组的原因是什么吗? 为了利用索引快速的查找!

如果我们试图指望利用链表来扩容的话, 当一个存储桶的中的链表越来越大, 在这个链表上的查找性能就会很差(退化成顺序查找了)

为此, 在数组容量不足时, 为了继续维持利用数组索引查找的优良性能, 我们必须对数组进行扩容.

链表存在的意义只是为了解决hash冲突, 而不是为了增大容量. 事实上, 我们希望链表的长度越短越好, 或者最好不要出现链表.

每次扩容扩多大

上一节我们讨论了扩容的时机, 接下来的另一问题就是每次多增加多少空间.

我们知道, 数组的扩容是一个很耗费CPU资源的动作, 需要将原数组的内容复制到新数组中去, 因此频繁的扩容必然会导致性能降低, 所以不可能数组满了之后, 每多加一个node, 我们就扩容一次.
但是, 一次扩容太大, 导致大量的存储空间用不完, 势必又造成很大的浪费, 因此, 必须根据实际情况设定一个合理的扩容大小.

在HashMap的实现中, 每次扩容我们都会将新数组的大小设为原数组大小的两倍.

总结

关于HashMap的设计思路, 我们可以用一句话来概括:

不忘初心 !

我们设计HashMap的初心是什么呢, 是找到一种方法, 可以存储一组键值对的集合, 并实现快速的查找.

==> 为了实现快速查找, 我们选择了数组而不是链表. 以利用数组的索引实现o(1)复杂度的查找效率.

==> 为了利用索引查找, 我们引入Hash算法, 将 key 映射成数组下标: key -> Index

==> 引入Hash算法又导致了Hash冲突

==> 为了解决Hash冲突, 我们采用链地址法, 在冲突位置转为使用链表存储.

==> 链表存储过多的节点又导致了在链表上节点的查找性能的恶化

==> 为了优化查找性能, 我们在链表长度超过8之后转而将链表转变成红黑树, 以将 o(n)复杂度的查找效率提升至o(log n)

可见, 每一次结构的调整, 都是始终围绕我们的初心:

实现快速的查找

来进行的, 始终不忘这一点, 在每一次出现问题的时候, 一切的选择是不是看起来就很自然了?(≧∇≦)ﾉ

(完)

下一篇: 深入理解HashMap(二): 关键源码逐行分析之hash算法

查看更多系列文章：系列文章目录