时间复杂度和空间复杂度

时间复杂度

执行算法所需的计算工作量。一般来说，计算机算法是问题规模n的函数f(n),算法的时间复杂度也因此记做T(n)=O(f(n));
常见时间复杂度有:常数阶、线性阶、平方阶、立方阶、对数阶、nlog2n阶、指数阶
效率：O(1) > O(log2n)> o(n)> o(nlog2n) > o(n^2) > o(n^3) > o(2^n) > o(n!) > o(n^n)

其他概念

• 最坏情况：最坏情况时的运行时间，一种保证。如果没有特别说明，说的时间复杂度即为最坏情况的时间复杂度

时间复杂度计算方式

举例：计算1+2+3+....+n的和

$sum=0

for($i=1;$i<=$n;$i++){
   $sum+=$i
}

可以看到循环了n次，所以时间复杂度就是O(n), 时间复杂度就是程序计算次数

其他说明

1.用常数1来取代所有时间中的所有加法常数

比如上面的例子中，不管n为多少，计算次数都是3，那么时间复杂度为O(1),而不是O(3)

2.在修改后的运行次数函数中，只保留最高阶项

比如运算的次数为n^2+1,那么为时间复杂度为o(n^2)

3.如果最高阶存在且不是1，则去除与这个项相乘的常数

2n^2+3n+1 ->n^2

为什么会去掉这些值，看下图

当计算量随着次数原来越大的时候，n和1的区别不是太大，而n^2曲线变得越来越大，所以这也是2n^2+3n+1 ->n^2最后会估量成n^2的原因,因为3n+1随着计算次数变大，基本可以忽略不计，其他都类似

常数阶 O(1)

function test($n){
    echo $n;
    echo $n;
    echo $n;
}

不管$n是多少，只运行3次，那么时间复杂度就是O(3),取为O(1)

线性阶 O(n)

for($i=1;$i<=$n;$i++){
    $sum+=$i
}

平(立)方阶：o(n^2)/o(n^3)

$sum=0;
for($i=1;$i<=$n;$i++){
    for($j=1;$j<$n;$j++){
    $sum+=$j
    }
}

两次循环，里面循环执行了n次，外层循环也执行了n次，所以时间复杂度为O(n^2),立方阶一样

特殊平方阶：O(n^2/2+n/2)->O(n^2)

for(){
    for(){
    .....            ----------->n^2
    }
}
                                  +
for(){
                     ------------> n
}

                                  +
                                 
echo $a+$b         --------------> 1

所以整体上计算次数为n^2+n+1,我们算时间复杂度为O(n^2)

对数阶：O(log2n)

while($n>=1){
    $n=$n/2;
}

n    执行次数
1      1
2      2
3      2

规律：

第一次     第二次       第三次      第四次      第五次
20--------->10---------->5-------->2.5------->1
n          n/2        n/2/2      n/2/2/2    n/2/2/...

所有规律:n/(2^m)=1;我们需要算出m, 转换成n=2^m,得出m=log2n,所以时间复杂度为O(logn)或者O(log2n)

空间复杂度

算法需要消耗的内存空间。即为S(n)=O(f(n));包括程序代码所占用的空间，输入数据所占用的空间和辅助变量所占用的空间这三个方面。计算和表达方式与时间复杂度类似，一般用复杂度的渐近性来表示

关于O(1)的问题， O(1)是说数据规模和临时变量数目无关，并不是说仅仅定义一个临时变量。举例：无论数据规模多大，我都定义100个变量，这就叫做数据规模和临时变量数目无关。就是说空间复杂度是O(1)。

空间复杂度计算方式

举例：冒泡排序的元素交换，空间复杂度O(1)
冒泡排序就是两两交换，中间设置临时变量存储交换的值，不管要交换的数据多大，临时变量始终为固定数量

冒泡排序:把$arr=[1,3,2,4,6,5]排序出来

原理：两两相邻的数进行比较，如果反序就交换，否则不交换
1     3     2     4    6     5

首先1和3比较，不动
1     3     2     4    6     5

再次3和2比较，交换
1     2     3    4    6     5

再次3和4比较，不动
1     2     3    4    6     5

再次4和6比较，不动
1     2     3    4    6     5

再次6和5比较，交换
1     2     3    4    5     6

for($i=0;$i<=$n;$i++){
    for($j=0;$j<=$n;$j++){
    
    if($arr[$j]>$arr[$j+1]){
       $tmp=$arr[$j]; 
      $arr[$j]=$arr[$j+1];
      $arr[$j+1]=$tmp;
    }
    }
}

所以时间复杂度为O(n^2),空间复杂度为O(1)

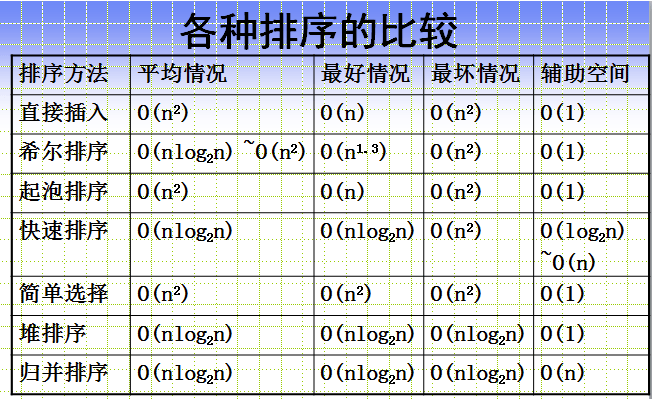
常见排序算法

冒泡排序、直接插入排序、希尔排序、选择排序、快速排序、对排序、归并排序

常见查找算法

二分查找、顺序查找

扩展：函数的渐进增长

https://blog.csdn.net/raylee2...