Immutable.js 采用了持久化数据结构和结构共享,保证每一个对象都是不可变的,任何添加、修改、删除等操作都会生成一个新的对象,且通过结构共享等方式大幅提高性能。
网上已经有很多文章简单介绍了 Immutable.js 的原理,但基本都是浅尝辄止,我也是搜了很久没找到针对 Immutable.js 原理的相对深入详细的文章,中英文都没有,针对 Clojure 或 Go 中持久化数据结构实现的文章倒是有一些。本文会集合多方资料以及我自己的一些理解,深入一些探究 Immutable.js 实现机制。文章可能会分2-3篇完成。
Immutable.js 部分参考了 Clojure 中的PersistentVector的实现方式,并有所优化和取舍,本文的一些内容也是基于它,想了解的可以阅读这里(共五篇,这是第一篇)
简单的例子
在深入研究前,我们先看个简单的例子:
let map1 = Immutable.Map({});
for (let i = 0; i < 800; i++) {
map1 = map1.set(Math.random(), Math.random());
}
console.log(map1);这段代码先后往map里写入了800对随机生成的key和value。我们先看一下控制台的输出结果,对它的数据结构有个大致的认知(粗略扫一眼就行了):
可以看到这是一个树的结构,子节点以数组的形式放在nodes属性里,nodes的最大长度似乎是32个。这里的bitmap涉及到对于树宽度的压缩,这些后面会说。
其中一个节点层层展开后长这样:
这个ValueNode存的就是一组值了,entry[0]是key,entry[1]是value。
大致看个形状就行了,下面来由浅入深研究一下。
基本原理
我们先看下维基对于持久化数据结构的定义:
In computing, a persistent data structure is a data structure that always preserves the previous version of itself when it is modified.
通俗点解释就是,对于一个持久化数据结构,每次修改后我们都会得到一个新的版本,且旧版本可以完好保留。
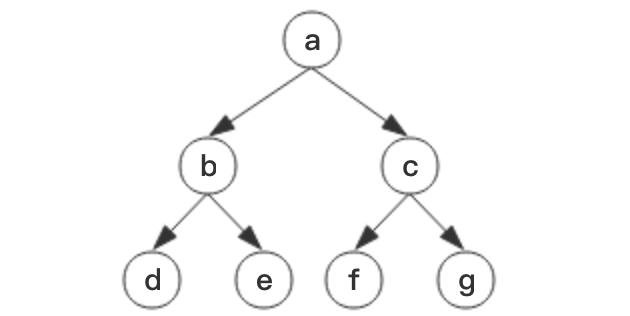
Immutable.js 用树实现了持久化数据结构,先看下图这颗树:
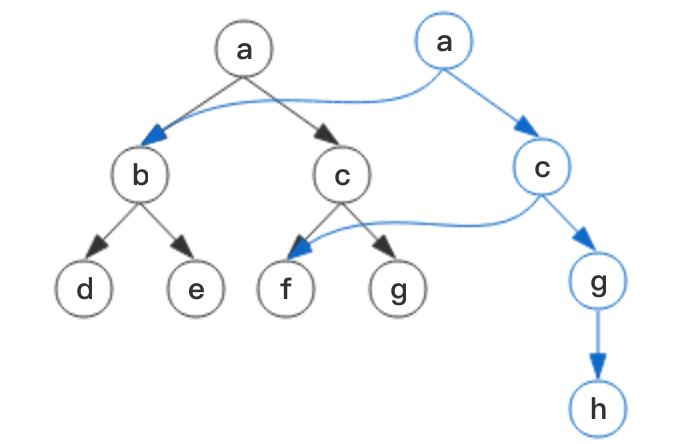
假如我们要在g下面插入一个节点h,如何在插入后让原有的树保持不变?最简单的方法当然是重新生成一颗树:
但这样做显然是很低效的,每次操作都需要生成一颗全新的树,既费时又费空间,因而有了如下的优化方案:
我们新生成一个根节点,对于有修改的部分,把相应路径上的所有节点重新生成,对于本次操作没有修改的部分,我们可以直接把相应的旧的节点拷贝过去,这其实就是结构共享。这样每次操作同样会获得一个全新的版本(根节点变了,新的a!==旧的a),历史版本可以完好保留,同时也节约了空间和时间。
至此我们发现,用树实现持久化数据结构还是比较简单的,Immutable.js提供了多种数据结构,比如回到开头的例子,一个map如何成为持久化数据结构呢?
Vector Trie
实际上对于一个map,我们完全可以把它视为一颗扁平的树,与上文实现持久化数据结构的方式一样,每次操作后生成一个新的对象,把旧的值全都依次拷贝过去,对需要修改或添加的属性,则重新生成。这其实就是Object.assign,然而这样显然效率很低,有没有更好的方法呢?
在实现持久化数据结构时,Immutable.js 参考了Vector Trie这种数据结构(其实更准确的叫法是persistent bit-partitioned vector trie或bitmapped vector trie,这是Clojure里使用的一种数据结构,Immutable.js 里的相关实现与其很相似),我们先了解下它的基本结构。
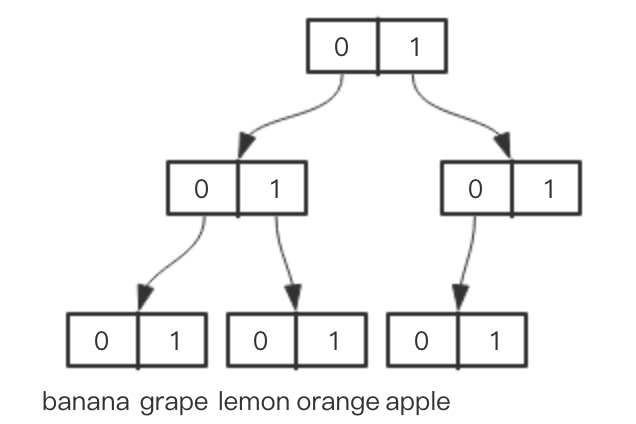
假如我们有一个 map ,key 全都是数字(当然你也可以把它理解为数组){0: 'banana', 1: 'grape', 2: 'lemon', 3: 'orange', 4: 'apple'},为了构造一棵二叉Vector Trie,我们可以先把所有的key转换为二进制的形式:{'000': 'banana', '001': 'grape', '010': 'lemon', '011': 'orange', '100': 'apple'},然后如下图构建Vector Trie:
可以看到,Vector Trie的每个节点是一个数组,数组里有0和1两个数,表示一个二进制数,所有值都存在叶子节点上,比如我们要找001的值时,只需顺着0 0 1找下来,即可得到grape。那么想实现持久化数据结构当然也不难了,比如我们想添加一个5: 'watermelon':
可见对于一个 key 全是数字的map,我们完全可以通过一颗Vector Trie来实现它,同时实现持久化数据结构。如果key不是数字怎么办呢?转成数字就行了。 Immutable.js 实现了一个hash函数,可以把一个值转换成相应数字。
这里为了简化,每个节点数组长度仅为2,这样在数据量大的时候,树会变得很深,查询会很耗时,所以可以扩大数组的长度,Immutable.js 选择了32。为什么不是31?40?其实数组长度必须是2的整数次幂,这里涉及到实现Vector Trie时的一个优化,接下来我们先研究下这点。
数字分区(Digit partitioning)
数字分区指我们把一个 key 作为数字对应到一棵前缀树上,正如上节所讲的那样。
假如我们有一个 key 9128,以 7 为基数,即数组长度是 7,它在Vector Trie里是这么表示的:
需要5层数组,我们先找到3这个分支,再找到5,之后依次到0。为了依次得到这几个数字,我们可以预先把9128转为7进制的35420,但其实没有这个必要,因为转为 7 进制形式的过程就是不断进行除法并取余得到每一位上的数,我们无须预先转换好,类似的操作可以在每一层上依次执行。
运用进制转换相关的知识,我们可以采用这个方法key / radixlevel - 1 % radix得到每一位的数(为了简便,本文除代码外所有/符号皆表示除法且向下取整),其中radix是每层数组的长度,即转换成几进制,level是当前在第几层,即第几位数。比如这里key是9128,radix是7,一开始level是5,通过这个式子我们可以得到第一层的数3。
代码实现如下:
const RADIX = 7;
function find(key) {
let node = root; // root是根节点,在别的地方定义了
// depth是当前树的深度。这种计算方式跟上面列出的式子是等价的,但可以避免多次指数计算
for (let size = Math.pow(RADIX, (depth - 1)); size > 1; size /= RADIX) {
node = node[Math.floor(key / size) % RADIX];
}
return node[key % RADIX];
}位分区(Bit Partitioning)
显然,以上数字分区的方法是有点耗时的,在每一层我们都要进行两次除法一次取模,显然这样并不高效,位分区就是对其的一种优化。位分区实际上是数字分区的一个子集,所有以2的整数次幂(2,4,8,16,32...)为基数的数字分区前缀树,都可以转为位分区。基于一些位运算相关的知识,我们就能避免一些耗时的计算。数字分区把 key 拆分成一个个数字,而位分区把 key 分成一组组 bit。比如一个 32 路的前缀树,数字分区的方法是把 key 以 32 为基数拆分(实际上就是32进制),而位分区是把它以 5bit 拆分,实际上就是把 32 进制数的每一位看做 5 个 bit ,或者说把 32 进制数看做2进制进行操作,这样原本的很多计算就可以用更高效的位运算的方式代替。因为现在基数是 32,即radix为 32,所以前面的式子现在是key / 32level - 1 % 32,而 32 又可以写作25,那么该式子可以转成这样key / 25 × (level - 1) % 25。根据位运算相关的知识我们知道a / 2n === a >>> n 、a % 2n === a & 2n-1。
其实举个例子最好理解:比如数字666666的二进制形式是10100 01011 00001 01010,这是一个20位的二进制数。如果我们要得到第二层那五位数01011,我们可以先把它右移>>>(左侧补0)10位,得到00000 00000 10100 01011,再&一下00000 00000 00000 11111,就得到了01011。
这样我们可以得到下面的代码:
const SHIFT = 5;
const WIDTH = 1 << SHIFT, // 32
const MASK = WIDTH - 1; // 31,即11111
function find(key) {
let node = root;
for (let shift = (depth - 1) * SHIFT; shift > 0; shift -= SHIFT) {
node = node[(key >>> shift) & MASK];
}
return node[key & MASK];
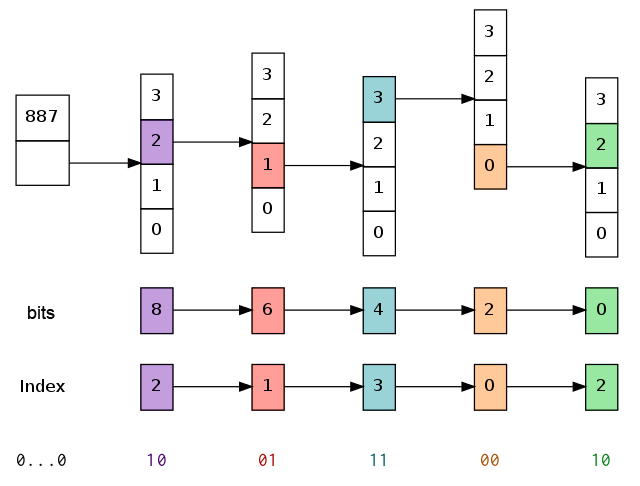
}这样我们每次查找的速度就会得到提升。可以看一张图进行理解,为了简化展示,假设我们只有2位分区即4路的前缀树,对于626,我们的查找过程如下:
626的二进制形式是10 01 11 00 10,所以通过以上的位运算,我们便依次得到了10、01...
源码
说了这么多,我们看一下 Immutable.js 的源码吧。虽然具体的代码较长,但主要看一下查找的部分就够了,这是Vector Trie的核心。
get(shift, keyHash, key, notSetValue) {
if (keyHash === undefined) {
keyHash = hash(key);
}
const idx = (shift === 0 ? keyHash : keyHash >>> shift) & MASK;
const node = this.nodes[idx];
return node
? node.get(shift + SHIFT, keyHash, key, notSetValue)
: notSetValue;
}可以看到, Immutable.js 也正是采用了位分区的方式,通过位运算得到当前数组的 index 选择相应分支。
不过它的实现方式与上文所讲的有一点不同,上文中对于一个 key ,我们是“正序”存储的,比如上图那个626的例子,我们是从根节点往下依次按照10 01 11 00 10去存储,而 Immutable.js 里则是“倒序”,按照10 00 11 01 10存储。所以通过源码这段你会发现 Immutable.js 查找时先得到的是 key 末尾的 SHIFT 个 bit ,然后再得到它们之前的 SHIFT 个 bit ,依次往前下去,而前面我们的代码是先得到 key 开头的 SHIFT 个 bit,依次往后。
至于为什么这么做,我一开始也没理解,但仔细想想这的确是最好的一种方式了,用这种方式的根本原因是key的大小(二进制长度)不固定,不固定的原因又是为了减小计算量,同时也能减小空间占用并让树更“平衡”。仔细思考一下的话,你应该能理解。关于这块内容,如果有时间我会放到之后的文章里说。
时间复杂度
因为采用了结构共享,在添加、修改、删除操作后,我们避免了将 map 中所有值拷贝一遍,所以特别是在数据量较大时,这些操作相比Object.assign有明显提升。
然而,查询速度似乎减慢了?我们知道 map 里根据 key 查找的速度是O(1),这里由于变成了一棵树,查询的时间复杂度变成了O(log N),准确说是O(log32 N)。
等等, 32 叉树?这棵树可不是一般地宽啊,Javascript里对象可以拥有的key的最大数量一般不会超过232个(ECMA-262第五版里定义了JS里由于数组的长度本身是一个 32 位数,所以数组长度不应大于 232 - 1 ,JS里对象的实现相对复杂,但大部分功能是建立在数组上的,所以在大部分场景下对象里 key 的数量不会超过 232 - 1。相关讨论见这里),这样就可以把查找的时间复杂度当做是“O(log32 232)”,差不多就是“O(log 7)”,所以我们可以认为在实际运用中,5bit (32路)的 Vector Trie 查询的时间复杂度是常数级的,32 叉树就是用了空间换时间。
空间...这个 32 叉树占用的空间也太大了吧?即便只有三层,我们也会有超过32 × 32 × 32 = 32768个节点。当然 Immutable.js 在具体实现时肯定不会傻乎乎的占用这么大空间,它对树的高度和宽度都做了“压缩”,此外,还对操作效率进行了其它一些优化,比如对 list 进行了“tail优化”。相关内容下一篇再讨论。
如果文章里有什么问题欢迎指正。
该文章是我正在更新的深入探究immutable.js系列的第一篇,我花了不少功夫才完成这篇文章,如果对你有帮助,希望能点个赞~
然后也请期待下一篇吧~预计一共会分2-3篇写完。该文章里有不懂的地方没关系,之后的文章会讨论更多内容,同时会有助于对该文章的理解。
第二篇更新到这里了:https://juejin.im/post/5ba4a6...
参考:
https://hypirion.com/musings/...
https://io-meter.com/2016/09/...
https://cdn.oreillystatic.com...
https://michael.steindorfer.n...
https://github.com/facebook/i...





**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。