上篇内容有在介绍 Gin 的路由实现时提到了前缀树,这次我们稍微深入探究一下前缀树的实现。
本文以一道编程题为例,讲述前缀树的实现,以及前缀树的一种优化形态压缩前缀树。
MapSum 问题
LeetCode 上有一道编程题是这样的
实现一个 MapSum 类里的两个方法,insert 和 sum。
对于方法 insert,你将得到一对(字符串,整数)的键值对。字符串表示键,整数表示值。如果键已经存在,那么原来的键值对将被替代成新的键值对。
对于方法 sum,你将得到一个表示前缀的字符串,你需要返回所有以该前缀开头的键的值的总和。
示例 1:
输入: insert("apple", 3), 输出: Null
输入: sum("ap"), 输出: 3
输入: insert("app", 2), 输出: Null
输入: sum("ap"), 输出: 5前缀树
根据题意,我们定义的 MapSum 的数据结构为:
type MapSum struct {
char byte
children map[byte]*MapSum
val int
}
/** Initialize your data structure here. */
func Constructor() MapSum {
}
func (this *MapSum) Insert(key string, val int) {
}
func (this *MapSum) Sum(prefix string) int {
}假设输入数据为:
m := Constructor()
m.Insert("inter", 1)
m.Insert("inner", 2)
m.Insert("in", 2)
m.Insert("if", 4)
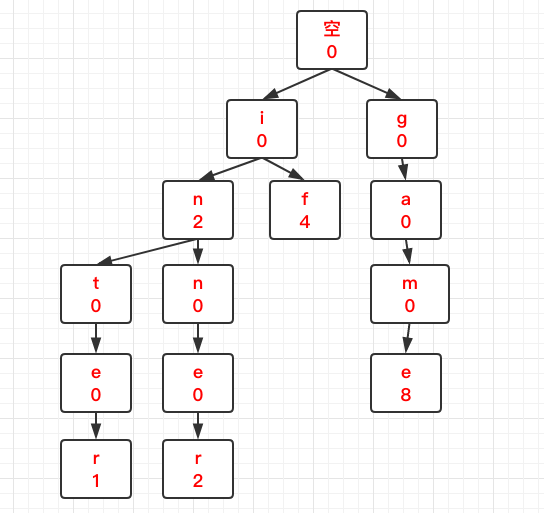
m.Insert("game", 8)则构造的前缀树应该是:
前缀树特性:
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符
- 从根节点到某一节点的路径上的字符连接起来,就是该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
Insert 函数
Insert 函数的签名:
func (this *MapSum) Insert(key string, val int)我们把 this 当做父节点,当插入的 key 长度为 1 时,则直接说明 key 对应的节点应该是 this 的孩子节点。
if len(key) == 1 {
for i, m := range this.children {
// c 存在与孩子节点
// 直接更新
if i == c {
m.val = val
return
}
}
// 未找到对应孩子
// 直接生成新孩子
this.children[c] = &MapSum{
char: c,
val: val,
children: make(map[byte]*MapSum),
}
return
}当插入的 key 长度大于 1,则寻找 key[0] 对应的子树,如果不存在,则插入新孩子节点;设置 this = this.children[key[0]] 继续迭代;
c := key[0]
for i, m := range this.children {
if i == c {
key = key[1:]
this = m
continue walk
}
}
// 未找到节点
this.children[c] = &MapSum{
char: c,
val: 0,
children: make(map[byte]*MapSum),
}
this = this.children[c]
key = key[1:]
continue walkSum 函数
Sum 函数签名:
func (this *MapSum) Sum(prefix string) intSum 函数的基本思想为:先找到前缀 prefix 对应的节点,然后统计以该节点为树根的的子树的 val 和。
// 先找到符合前缀的节点
// 然后统计和
for prefix != "" {
c := prefix[0]
var ok bool
if this, ok = this.children[c]; ok {
prefix = prefix[1:]
continue
} else{
// prefix 不存在
return 0
}
}
return this.sumNode()sumNode 函数统计了子树的 val 和,使用递归遍历树:
s := this.val
for _, child := range this.children{
s += child.sumNode()
}
return s以上是一种标准的前缀树的做法。当字符串公用的节点比较少的时候,对于每个字符都要创建单独的节点,有点浪费空间。有一种压缩前缀树的算法,在处理前缀树问题的时候能够使用更少的节点。
压缩前缀树
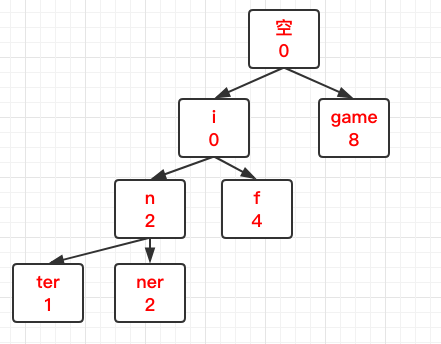
对与上面的例子来说,压缩前缀树是这样的结果:
对于该例子来说,明显少了很多节点。另外,我们的 MapSum 结构体也稍微有了变化:
type MapSum struct {
// 之前的 char byte 变成了 key string
key string
children map[byte]*MapSum
val int
}Insert
压缩前缀树与前缀树的实现不同点在于节点的分裂。比如,当树中已经存在 "inner", "inter" 的情况加,再加入 "info" 时,原 "in" 节点需要分裂成 "i" -> "n" 两个节点,如图:
在 Insert 时,需要判断当前插入字符串 key 与 节点字符串 this.key 的最长公共前缀长度 n:
minLen := min(len(key), len(this.key))
// 找出最长公共前缀长度 n
n := 0
for n < minLen && key[n] == this.key[n] {
n ++
}然后拿 n 与 len(this.key) 比较,如果比 this.key 长度短,则 this.key 需要分裂,否则,不需要分裂。
this 节点分裂逻辑:
// 最前公共前缀 n < len(this.key)
// 则该节点需要分裂
child := &MapSum{
val: this.val,
key: this.key[n:],
children: this.children,
}
// 更新当前节点
this.key = this.key[:n]
this.val = 0
this.children = make(map[byte]*MapSum)
this.children[child.key[0]] = child然后再判断 n 与 len(key),如果 n == len(key),则说明 key 对应该节点。直接更新 val
if n == len(key) {
this.val = val
return
}n < len(key) 时,如果有符合条件子树,则继续迭代,否则直接插入孩子节点:
key = key[n:]
c := key[0]
// 如果剩余 子key 的第一个字符存在与 children
// 则继续向下遍历树
if a, ok := this.children[c]; ok {
this = a
continue walk
} else{
// 否则,新建节点
this.children[c] = &MapSum{
key: key,
val: val,
children: make(map[byte]*MapSum),
}
return
}以上是压缩前缀树的做法。
算法优化
上述 MapSum 的 children 使用的是 map,但是 map 一般占用内存较大。可以使用 节点数组children + 节点前缀数组 indices 的方式维护子节点,其中 indices 与 children 一一对应。
此时的结构体应该是这样的:
type MapSum struct {
key string
indices []byte
children []*MapSum
val int
}查找子树时,需要拿 key[:n][0] 与 indices 中的字符比较,找到下标后继续迭代子树;未找到时插入子树即可。
以上。
Y_xx
相关内容:

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。