二叉树的前序，中序，后序遍历方法总结

前言

二叉树的前序遍历，中序遍历，后序遍历是面试中常常考察的基本算法，关于它的概念这里不再赘述了，还不了解的同学可以去翻翻LeetCode的解释。

这里，我个人对这三个遍历顺序理解是：前 中 后 这三个词是针对根节点的访问顺序而言的，即前序就是根节点在最前根->左->右，中序是根节点在中间左->根->右，后序是根节点在最后左->右->根。

无论哪种遍历顺序，用递归总是最容易实现的，也是最没有含金量的。但我们至少要保证能信手捏来地把递归写出来，在此基础上，再掌握非递归的方式。

在二叉树的顺序遍历中，常常会发生先遇到的节点到后面再访问的情况，这和先进后出的栈的结构很相似，因此在非递归的实现方法中，我们最常使用的数据结构就是栈。

前序遍历

前序遍历（题目见这里）是三种遍历顺序中最简单的一种，因为根节点是最先访问的，而我们在访问一个树的时候最先遇到的就是根节点。

递归法

递归的方法很容易实现，也很容易理解：我们先访问根节点，然后递归访问左子树，再递归访问右子树，即实现了根->左->右的访问顺序，因为使用的是递归方法，所以每一个子树都实现了这样的顺序。

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        preorderHelper(root, result);
        return result;
    }

    private void preorderHelper(TreeNode root, List<Integer> result) {
        if (root == null) return;
        result.add(root.val); // 访问根节点
        preorderHelper(root.left, result); // 递归遍历左子树
        preorderHelper(root.right, result); //递归遍历右子树
    }
}

迭代法

在迭代法中，我们使用栈来实现。由于出栈顺序和入栈顺序相反，所以每次添加节点的时候先添加右节点，再添加左节点。这样在下一轮访问子树的时候，就会先访问左子树，再访问右子树：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        if (root == null) return result;

        Stack<TreeNode> toVisit = new Stack<>();
        toVisit.push(root);
        TreeNode cur;

        while (!toVisit.isEmpty()) {
            cur = toVisit.pop();
            result.add(cur.val); // 访问根节点
            if (cur.right != null) toVisit.push(cur.right); // 右节点入栈
            if (cur.left != null) toVisit.push(cur.left); // 左节点入栈
        }
        return result;
    }
}

中序遍历

中序遍历（题目见这里）相对前序遍历要复杂一点，因为我们说过，在二叉树的访问中，最先遇到的是根节点，但是在中序遍历中，最先访问的不是根节点，而是左节点。（当然，这里说复杂是针对非递归方法而言的，递归方法都是很简单的。）

递归法

无论对于哪种方式，递归的方法总是很容易实现的，也是很符合直觉的。对于中序遍历，就是先访问左子树，再访问根节点，再访问右子树，即 左->根->右：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        inorderHelper(root, result);
        return result;
    }
    
    private void inorderHelper(TreeNode root, List<Integer> result) {
        if(root == null) return;
        inorderHelper(root.left, result); // 递归遍历左子树
        result.add(root.val); // 访问根节点
        inorderHelper(root.right, result); // 递归遍历右子树
    }
}

大家可以对比它和前序遍历的递归实现，二者仅仅是在节点的访问顺序上有差别，代码框架完全一致。

迭代法

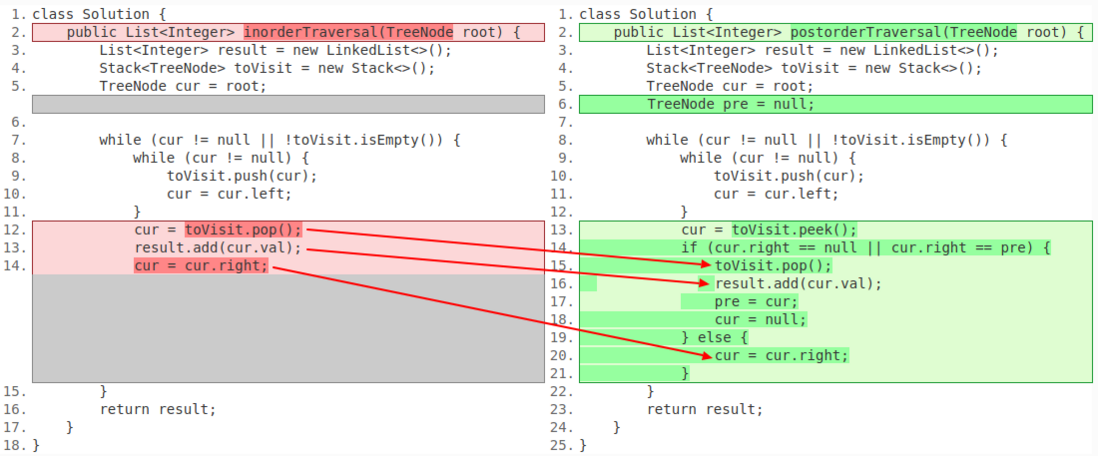
中序遍历的迭代法要稍微复杂一点，因为最先遇到的根节点不是最先访问的，我们需要先访问左子树，再回退到根节点，再访问根节点的右子树，这里的一个难点是从左子树回退到根节点的操作，虽然可以用栈来实现回退，但是要注意在出栈时保存根节点的引用，因为我们还需要通过根节点来访问右子树：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> toVisit = new Stack<>();
        TreeNode cur = root;

        while (cur != null || !toVisit.isEmpty()) {
            while (cur != null) {
                toVisit.push(cur); // 添加根节点
                cur = cur.left; // 循环添加左节点
            }
            cur = toVisit.pop(); // 当前栈顶已经是最底层的左节点了，取出栈顶元素，访问该节点
            result.add(cur.val);
            cur = cur.right; // 添加右节点
        }
        return result;
    }
}

这里：

while (cur != null) {
    toVisit.push(cur); 
    cur = cur.left; 
}

↑这一部分实现了递归添加左节点的作用。

cur = toVisit.pop();
result.add(cur.val);
cur = cur.right;

↑这一部分实现了对根节点的遍历，同时将指针指向了右子树，在下轮中遍历右子树。

在看这部分代码中，脑海中要有一个概念：当前树的根节点的左节点，是它的左子树的根节点。因此从不同的层次上看，左节点也是根节点。另外，LeetCode上也提供了关于中序遍历的动态图的演示，感兴趣的读者可以去看一看。

后序遍历

后序遍历（题目见这里）是三种遍历方法中最难的，与中序遍历相比，虽然都是先访问左子树，但是在回退到根节点的时候，后序遍历不会立即访问根节点，而是先访问根节点的右子树，这里要小心的处理入栈出栈的顺序。（当然，这里说复杂是针对非递归方法而言的，递归方法都是很简单的。）

递归法

无论对于哪种方式，递归的方法总是很容易实现的，也是很符合直觉的。对于后序遍历，就是先访问左子树，再访问右子树，再访问根节点，即 左->右->根：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        postorderHelper(root, result);
        return result;
    }

    private void postorderHelper(TreeNode root, List<Integer> result) {
        if (root == null) return;
        postorderHelper(root.left, result); // 遍历左子树
        postorderHelper(root.right, result); // 遍历右子树
        result.add(root.val); // 访问根节点
    }
}

与前序遍历和后序遍历相比，代码结构完全一致，差别仅仅是递归函数的调用顺序。

迭代法

前面说过，与中序遍历不同的是，后序遍历在访问完左子树向上回退到根节点的时候不是立马访问根节点的，而是得先去访问右子树，访问完右子树后在回退到根节点，因此，在迭代过程中要复杂一点：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> toVisit = new Stack<>();
        TreeNode cur = root;
        TreeNode pre = null;

        while (cur != null || !toVisit.isEmpty()) {
            while (cur != null) {
                toVisit.push(cur); // 添加根节点
                cur = cur.left; // 递归添加左节点
            }
            cur = toVisit.peek(); // 已经访问到最左的节点了
            //在不存在右节点或者右节点已经访问过的情况下，访问根节点
            if (cur.right == null || cur.right == pre) { 
                toVisit.pop();
                result.add(cur.val);
                pre = cur;
                cur = null;
            } else {
                cur = cur.right; // 右节点还没有访问过就先访问右节点
            }
        }
        return result;
    }
}

这里尤其注意后续遍历和中序遍历中对于从最左侧节点向上回退时的处理：

在后序遍历中，我们首先使用的是：

cur = toVisit.peek();

注意，这里使用的是peek而不是pop，这是因为我们需要首先去访问右节点，下面的：

if (cur.right == null || cur.right == pre) 

就是用来判断是否存在右节点，或者右节点是否已经访问过了，如果右节点已经访问过了，则接下来的操作就和中序遍历的情况差不多了，所不同的是，这里多了两步：

pre = cur;
cur = null;

这两步的目的都是为了在下一轮遍历中不再访问自己，cur = null很好理解，因为我们必须在一轮结束后改变cur的值，以添加下一个节点，所以它和cur = cur.right一样，目的都是指向下一个待遍历的节点，只是在这里，右节点已经访问过了，则以当前节点为根节点的整个子树都已经访问过了，接下来应该回退到当前节点的父节点，而当前节点的父节点已经在栈里了，所以我们并没有新的节点要添加，直接将cur设为null即可。

pre = cur 的目的有点类似于将当前节点标记为已访问，它是和if条件中的cur.right == pre配合使用的。注意这里的两个cur指的不是同一个节点。我们假设当前节点为C，当前节点的父节点为A，而C是A的右孩子，则当前cur是C，但在一轮中，cur将变成A，则：

         A 
        / \
       B   C (pre)

• pre = cur 就是 pre = C
• if (cur.right == null || cur.right == pre) 就是 if (A.right == null || A.right == pre)

这里，由于A是有右节点的，它的右节点就是C，所以A.right == null不成立。但是C节点我们在上一轮已经访问过了，所以这里为了防止进入else语句重复添加节点，我们多加了一个A.right == pre条件，它表示A的右节点已经访问过了，我们得以进入if语句内，直接访问A节点。

双栈法

前面我们说过，前序遍历之所以最简单，是因为遍历过程中最先遇到的根节点是最先访问的，而在后序遍历中，最先遇到的根节点是最后访问的，所以导致了上面的迭代法非常复杂，那有没有办法简化一下呢？其实是有的。

大家仔细观察一下后序遍历的顺序左->右->根，根节点在最后，要是能像前序遍历一样把它放在最前面就好了，怎么办呢？一个最简单的方法就是倒个序，即将左->右->根倒序成根->右->左，这样不就和前序遍历的根->左->右差不多了吗？而因为栈本身就是后进先出的，是天然的倒序工具，因此，我们只需要再用一个栈将输出顺序反过来即可，由此，双栈法应运而生，它的思路是：

1. 用一个栈实现 根->右->左 的遍历
2. 用另一个栈将遍历顺序反过来，使之变成 左->右->根

下面我们来看实现：

首先，在最开始的前序遍历中，我们已经实现了递归方式的根->左->右的遍历，如下：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        if (root == null) return result;

        Stack<TreeNode> toVisit = new Stack<>();
        toVisit.push(root);
        TreeNode cur;

        while (!toVisit.isEmpty()) {
            cur = toVisit.pop();
            result.add(cur.val); // 访问根节点
            if (cur.right != null) toVisit.push(cur.right); // 右节点入栈
            if (cur.left != null) toVisit.push(cur.left); // 左节点入栈
        }
        return result;
    }
}

那么要实现根->右->左的遍历，只需要交换左右节点的入栈顺序即可，即：
（代码中将与前序遍历相同的代码部分注释起来了，好让大家能直观地看到不同点，下同）

//class Solution {
//    public List<Integer> preorderTraversal(TreeNode root) {
//        List<Integer> result = new LinkedList<>();
//        if (root == null) return result;
//
//        Stack<TreeNode> toVisit = new Stack<>();
//        toVisit.push(root);
//        TreeNode cur;
//
//        while (!toVisit.isEmpty()) {
//            cur = toVisit.pop();
//            result.add(cur.val); // 访问根节点
              if (cur.left != null) toVisit.push(cur.left); // 左节点入栈
              if (cur.right != null) toVisit.push(cur.right); // 右节点入栈
//        }
//        return result;
//    }
//}

至此，我们完成了第一步，接下来是第二步，用另一个栈来反序：

//class Solution {
//    public List<Integer> postorderTraversal(TreeNode root) {
//        List<Integer> result = new LinkedList<>();
//        if (root == null) return result;
//
//        Stack<TreeNode> toVisit = new Stack<>();
          Stack<TreeNode> reversedStack = new Stack<>();
//        toVisit.push(root);
//        TreeNode cur;
//
//        while (!toVisit.isEmpty()) {
//            cur = toVisit.pop();
              reversedStack.push(cur);  // result.add(cur.val);
//            if (cur.left != null) toVisit.push(cur.left); // 左节点入栈
//            if (cur.right != null) toVisit.push(cur.right); // 右节点入栈
//        }
//
          while (!reversedStack.isEmpty()) {
              cur = reversedStack.pop();
              result.add(cur.val);
          }
//        return result;
//    }
//}

可见，反序只是将原来直接添加到结果中的值先添加到一个栈中，最后再将该栈中的元素全部出栈即可。

至此，我们就实现了双栈法的后序遍历，是不是变的和前序遍历一样简单了呢？

双栈法的简化——使用Deque

上面我们介绍的双栈法虽然简化了迭代法，但是它额外使用了一个栈，并且需要在最后将反序栈中的元素再一个个出栈，添加到结果集中，显得比较笨重，不够优雅，我们下面就来试着简化一下。

既然最后需要逆序输出，除了用额外的栈来实现，我们还可以用链表本身来实现——即，每次添加元素时都添加到链表的头部，这样，链表本身就成为了一个栈，在java中，LinkedList本身就已经实现了Deque接口，因此，它也可以当做双端队列，则，上面的代码可以简化成：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        LinkedList<Integer> result = new LinkedList<>();
        if (root == null) return result;

        Stack<TreeNode> toVisit = new Stack<>();
        toVisit.push(root);
        TreeNode cur;

        while (!toVisit.isEmpty()) {
            cur = toVisit.pop();
            result.addFirst(cur.val);
            if (cur.left != null) toVisit.push(cur.left);
            if (cur.right != null) toVisit.push(cur.right);
        }
        return result;
    }
}

如果你拿它和前序遍历的迭代法的代码对比可以发现，它们唯一的不同就在于这三行：

result.addFirst(cur.val);
if (cur.left != null) toVisit.push(cur.left); 
if (cur.right != null) toVisit.push(cur.right); 

这里要注意，addFirst方法是将值添加到链表的开头。

Morris遍历法

前面我们多次说过，在二叉树的访问中，我们最先遇到的是树的根节点，因此，前序遍历方法非常简单，因为它本身就是先去访问根节点，即根->左->右。而在后序遍历中，为了简化问题，我们出于同样的考虑，将后续遍历左->右->根的顺序先倒置成根->右->左，使得后续遍历中也先去访问根节点，这样就将后序遍历变得和前序遍历一样简单了，所以目前来看，反倒是中序遍历左->根->右变成最不直观的了。

那么有没有办法像转变后序遍历一样，将中序遍历也转变成先访问根节点呢？似乎不太容易，因为中序遍历的根节点是在中间访问的，无论正过来倒过去，都无法最先访问。

当然，万事不是绝对的，如果我们的二叉树是一个偏向二叉树，每一个子树都没有左节点呢？那么就有：

• 左->根->右 => 根->右

这样我们就能先访问根节点了。当然，这自然是个极端的例子，因为正常情况下二叉树都不会长这样。但是，这为我们提供了一个思路——既然二叉树不长这样，我们可以把它转换成这样，这也就是Morris遍历法所做的事情。

那么怎么转换呢，我们知道，中序遍历需要先去遍历左子树，而左子树中也要按左->根->右的顺序去遍历，所以整个树的根节点必然是接在左子树的最后一个右节点的后面去遍历，所以，Morris遍历法的算法伪代码如下：

current = root;
while(current != null) {
    if(current没有左节点) {
        访问current的值
        current = current.right
    }
    else {
        在current的左子树中找到最靠右的节点(rightmost node)
        将current接在这个rightmost node下面，作为它的右子树
        current = current.left
    }
}

这个伪代码看上去有点抽象，我们来看一个例子，这个例子来源于LeetCode：

现在有这么一棵二叉树：

          1
        /   \
       2     3
      / \   /
     4   5 6

我们要对它进行中序遍历，需要将它转换成一个只有右节点的偏向树，按照Morris算法，首先1是根节点，它是现在的current，它存在一个左子树：

         2
        / \
       4   5

按照算法，我们需要找到这个左子树最靠右的节点，在这里就是5，接下来就将current作为这个节点的右子树，即：

         2
        / \
       4   5
            \
             1
              \
               3
              /
             6

然后令current为原来根节点的左节点，则此时的current变成了2，则新的current还是存在左节点，在这里就是4，我们按照同样的步骤再将当前的current接在它的左子树的最右节点下面，这里左子树只有一个节点4，所以我们直接作为该节点的右孩子即可：

        4
         \
          2
           \
            5
             \
              1
               \
                3
               /
              6

到这里，4就没有左子树了，则我们进入if语句中，访问当前节点的值，再指向它的右子树。这样一路访问到3这个节点，我们发现它是有左子树6的，我们再按之前的方式，将3接在6的右子树上，最后完成遍历。

所以，综上看下来，Morris算法的目的就是消灭左子树，如果根节点存在左子树，就将根节点作为左子树的最右节点的右孩子，这是因为中序遍历中，对于根节点的访问，一定是在访问完左子树之后的，而左子树的最右节点就是左子树访问的最后一个节点，因为大家都按照左->中->右的顺序来遍历。

有了对上面的过程的理解以及伪代码，我们再来写代码就很容易了：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        TreeNode cur = root;
        while (cur != null) {
            if (cur.left == null) { 
                result.add(cur.val);
                cur = cur.right;
            } else {
                TreeNode rightmost = cur.left;
                while (rightmost.right != null) {
                    rightmost = rightmost.right; // 寻找左子树的最右节点
                }
                rightmost.right = cur; // 当前节点作为左子树的最右节点的右孩子
                TreeNode oldRoot = cur;
                cur = cur.left; // 将左子树作为新的顶层节点
                oldRoot.left = null; // 消除左子树，防止出现无限循环
            }
        }
        return result;
    }
}

这里一定要注意oldRoot.left = null，这一步的目的就是消除左子树，同时它也能防止无限循环的出现，一定不要忘记这一步。

综上，你可以把Morris算法理解成不断将左节点作为新的顶层节点从而消灭左子树的过程，即实现了：

• 左->根->右 => 根->右

的转变。

其实，如果你再倒回去看我们之前中序遍历的迭代法的做法：

while (cur != null || !toVisit.isEmpty()) {
    while (cur != null) {
        toVisit.push(cur); // 添加根节点
        cur = cur.left; // 循环添加左节点
    }
    cur = toVisit.pop(); // 当前栈顶已经是最底层的左节点了，取出栈顶元素，访问该节点
    result.add(cur.val);
    cur = cur.right; // 添加右节点
}

这里，不断添加左节点的做法也有点将左->根->右 转变成 根->右 的意思，因为以最左的那个左节点为根节点的树可不就是只剩下根->右了嘛，然后我们就安心地访问根节点，再去访问它的右节点了，只是在下一轮右节点的访问中，我们还是要不断地添加左节点，以实现“消灭”左节点的目的。可见，事实上，思想都是相通的。

最后，这里有一点特别值得一提的是，在Morris算法中，我们并没有使用到栈，因为我们已经将整个树调整成其访问顺序恰好和遍历顺序一致的偏向树了，所以相比之前使用栈的算法，这种算法更节约空间。

复杂度分析

前面我们分析了前序，中序，后序遍历的各种方法，但是并没有去分析它们的复杂度，这里我们一起来看一下：

首先对于时间复杂度，由于树的每一个节点我们都是要去遍历的，所以它是难以优化的，都是O(n)，对于Morris算法，这个复杂度的计算要稍微复杂一点，但是可以证明，它同样是O(n)。

对于空间复杂度，对递归方法而言，最坏的空间复杂度是O(n)，平均空间复杂度是O(log(n))。对于普通的迭代法而言，由于我们使用到了栈，其时间复杂度和空间复杂度一致，都是O(n)，对于Morris算法，由于我们并没有使用到栈，只使用到临时变量，因此其空间复杂度是O(1)。

总结

本文介绍了关于二叉树的前序，中序，后序遍历的递归和迭代两个版本的算法，同时对于后序遍历的简化版本及中序遍历的Morris算法做出了解释和说明，其实Morris算法的思想同样可以应用在前序遍历和后序遍历上，只是笔者认为前序遍历和后序遍历经过简化后已经足够简单，这里并没有给出，不然大有探讨“茴香豆的茴字有多少种写法”的嫌疑。

二叉树的遍历中重要的是理解节点的遍历顺序和访问顺序之间的关系，我们在上面的非递归算法中多次提到，由于最先访问的到的是树的根节点，所以很多优化都是将访问顺序转换成先访问根节点来做的，理解了这一点再去看那些“玄乎”但是能work的代码，就不会觉得摸不着头脑了。

(完)