贝塞尔曲线算法之JS获取点

什么是贝塞尔曲线？

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。

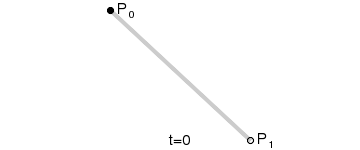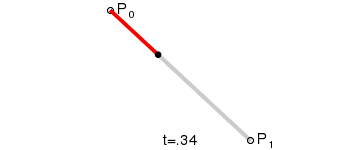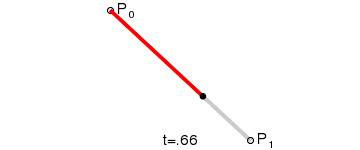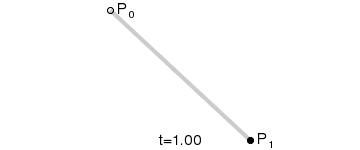
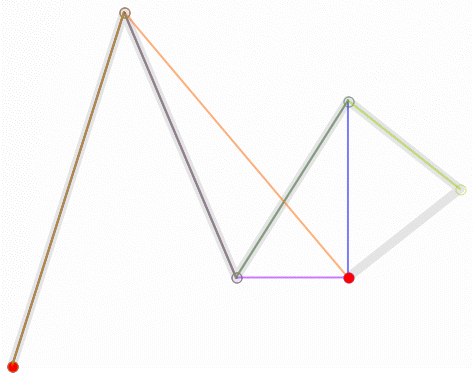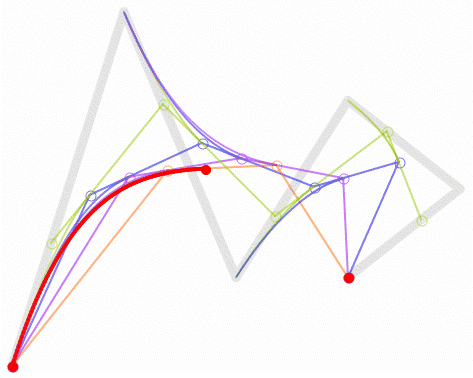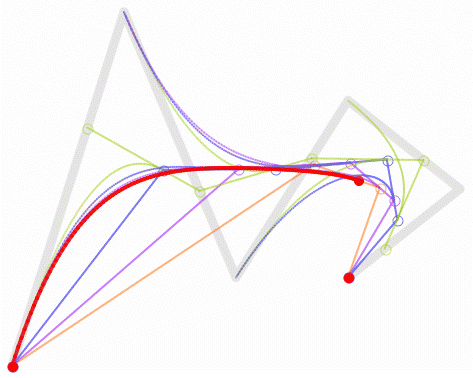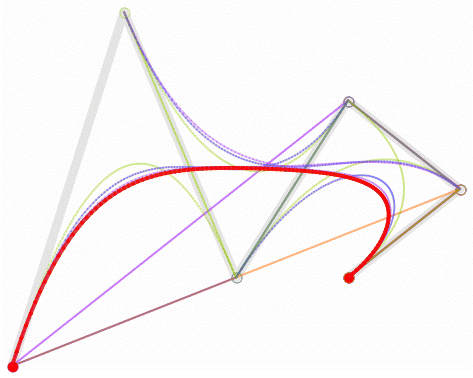
这个一阶贝塞尔曲线绘制过程，黑点按百分比t从P0->P1移动，看不出什么呢~ 那继续看后面的图

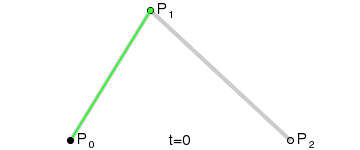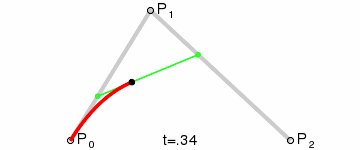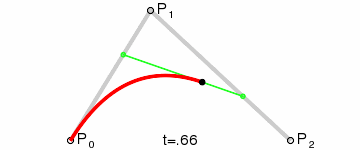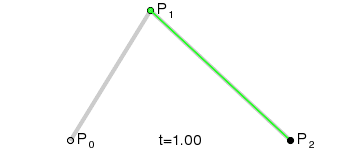
这个是二阶贝塞尔曲线，从P0->P1有个小绿点按百分比t运动，从P1->P2也有个小绿点按百分比t运动，两个绿点之间也有个小黑点按百分比t运动，这个黑点产生的轨迹就是一个二阶贝塞尔曲线。

这个是三阶贝塞尔曲线，同理，绿点有3个，点与点之间都是按百分比t运动，最终得到一个小黑点。这个小黑点的运动轨迹就是三阶贝塞尔。

同理，还有四阶贝塞尔。

同理，六阶贝塞尔，N阶贝塞尔。

实际上，我们的运用中，3阶贝塞尔就已经足够满足我们的业务需求了，生活中，多个三阶贝塞尔曲线可以组合成任意一条曲线，我们的photoshop里面的钢笔工具就是3阶贝塞尔曲线实现的。

贝塞尔曲线方程解析

数学家已经给了我们公式：

不好意思，高数还给了老师，这尼玛公式看不懂啊~ 没关系，我们简化下就能看懂了。

// t是百分比，a是参数

// 1阶贝塞尔曲线公式
function onebsr(t, a1, a2) {
    return a1 + (a2 - a1) * t;
}

// 2阶贝塞尔曲线公式
function twobsr(t, a1, a2, a3) {
    return ((1 - t) * (1 - t)) * a1 + 2 * t * (1 - t) * a2 + t * t * a3;
}

// 3阶贝塞尔曲线公式
function threebsr(t, a1, a2, a3, a4) {
    return a1 * (1 - t) * (1 - t) * (1 - t) + 3 * a2 * t * (1 - t) * (1 - t) + 3 * a3 * t * t * (1 - t) + a4 * t * t * t;
}

根据公式，我们可以带入坐标进行计算

/**
     * @desc 一阶贝塞尔
     * @param {number} t 当前百分比
     * @param {Array} p1 起点坐标
     * @param {Array} p2 终点坐标
     */
    oneBezier(t, p1, p2) {
        const [x1, y1] = p1;
        const [x2, y2] = p2;
        let x = x1 + (x2 - x1) * t;
        let y = y1 + (y2 - y1) * t;
        return [x, y];
    }

    /**
     * @desc 二阶贝塞尔
     * @param {number} t 当前百分比
     * @param {Array} p1 起点坐标
     * @param {Array} p2 终点坐标
     * @param {Array} cp 控制点
     */
    twoBezier(t, p1, cp, p2) {
        const [x1, y1] = p1;
        const [cx, cy] = cp;
        const [x2, y2] = p2;
        let x = (1 - t) * (1 - t) * x1 + 2 * t * (1 - t) * cx + t * t * x2;
        let y = (1 - t) * (1 - t) * y1 + 2 * t * (1 - t) * cy + t * t * y2;
        return [x, y];
    }

    /**
     * @desc 三阶贝塞尔
     * @param {number} t 当前百分比
     * @param {Array} p1 起点坐标
     * @param {Array} p2 终点坐标
     * @param {Array} cp1 控制点1
     * @param {Array} cp2 控制点2
     */
    threeBezier(t, p1, cp1, cp2, p2) {
        const [x1, y1] = p1;
        const [x2, y2] = p2;
        const [cx1, cy1] = cp1;
        const [cx2, cy2] = cp2;
        let x =
            x1 * (1 - t) * (1 - t) * (1 - t) +
            3 * cx1 * t * (1 - t) * (1 - t) +
            3 * cx2 * t * t * (1 - t) +
            x2 * t * t * t;
        let y =
            y1 * (1 - t) * (1 - t) * (1 - t) +
            3 * cy1 * t * (1 - t) * (1 - t) +
            3 * cy2 * t * t * (1 - t) +
            y2 * t * t * t;
        return [x, y];
    }

算法封装

我把贝塞尔曲线封装了下，添加了一个获取路径点的方法，然后使用span标签绘制到页面上的效果。

我们看看DEMO中1~3阶贝塞尔曲线上获取点的效果

demo的github地址：https://github.com/mtsee/Bezier