数据结构与算法——二叉树(下)

1. 概述

前面的文章说到了二叉树，其实今天讲的二叉搜索(查找)树就是二叉树最常用的一种形式，它支持高效的查找、插入、删除操作，它的定义是这样的：对于树中的任意一个节点，其左子节点值必须小于该节点，其右子节点必须大于该节点。例如下图中的几种树都是二叉查找树：

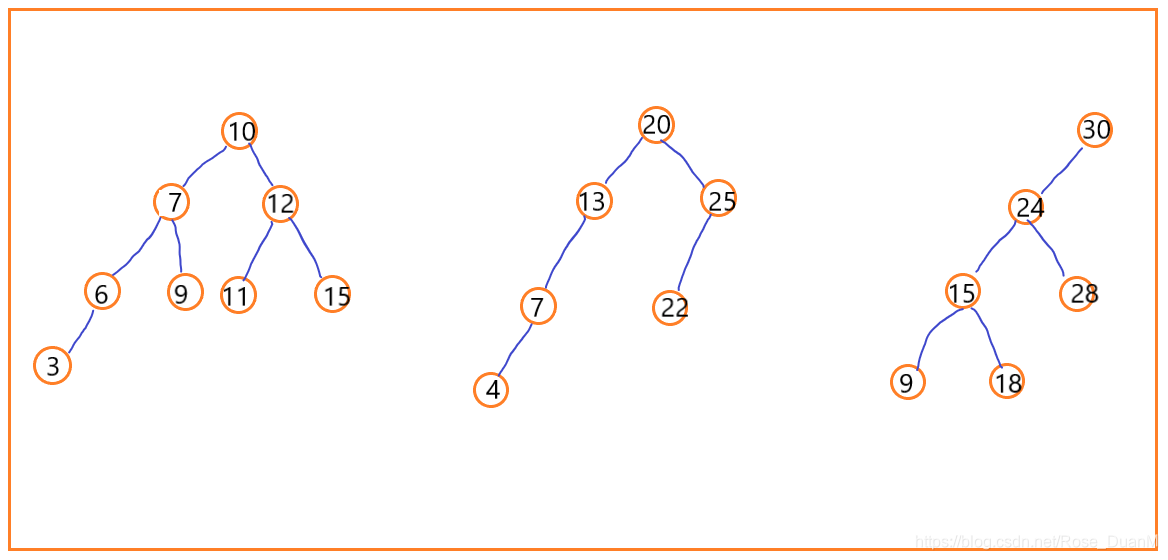
2. 二叉搜索树的查找

我们直接拿查找的数据和根节点数据作比较，如果大于根节点，则在右子树中递归查找，如果小于根节点，则在左子树中查找，如果等于，则直接返回。就像下图的查找过程：

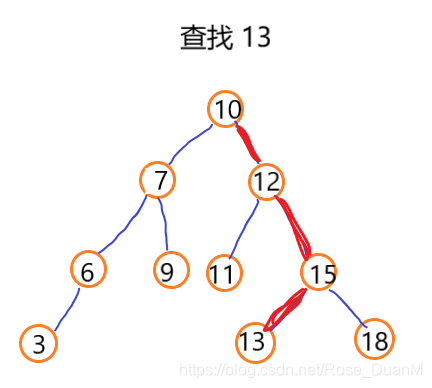
结合代码能够更直观的理解：

public class BinaryTree {
    private Node head = null;//树的根节点
    //1.查找节点
    public Node find(int value){
        Node p = head;
        while (p != null){
            if (p.getData() > value) p = p.left;
            else if (p.getData() < value) p = p.right;
            else return p;
        }
        return null;
    }
    //定义树的节点
    public static class Node{
        private int data;
        private Node left;
        private Node right;

        public Node(int data) {
            this.data = data;
            this.left = null;
            this.right = null;
        }

        public int getData() {
            return data;
        }
    }
}

3. 二叉搜索树的插入

插入操作和查找其实比较的类似，都是需要拿插入的数据和树中的数据进行比较，如果插入的数据大于树节点数据，并且节点的右子树为空，则直接插入到右子树，否则继续在右子树中递归查找位置；如果插入的数据小于树节点数据，并且节点的左子树为空，则直接插入到左子树，否则继续在左子树中递归查找位置。

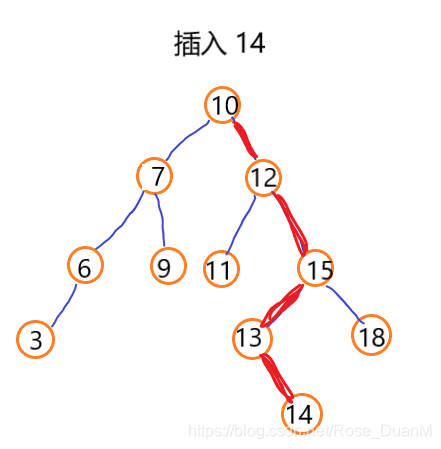
结合代码理解一下：

 public void insert(int value){
        Node node = new Node(value);
        if (head == null){
            head = node;
            return;
        }
        Node p = head;
        while (p != null){
            if (p.getData() > value){
                if (p.left == null) {
                    p.left = node;
                    return;
                }
                p = p.left;
            }
            else {
                if (p.right == null) {
                    p.right = node;
                    return;
                }
                p = p.right;
            }
        }
    }

4. 二叉搜索树的删除

前面的查找和插入操作都比较的简单易懂，但是二叉搜索树的删除操作就比较的复杂了，分为了几种情况。

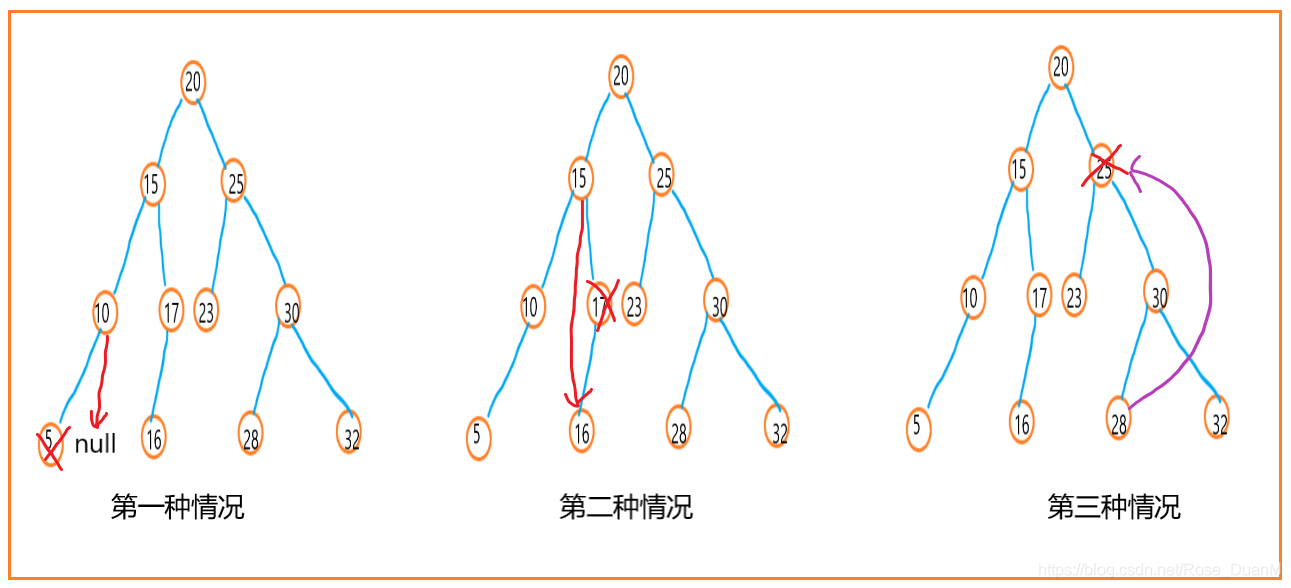
• 第一种情况：要删除的节点没有子节点，这样的话，可以直接将指向该节点的父节点指针设为 null。
• 第二种情况：要删除的节点只有一个子节点，直接将该节点的父节点的指针，指向该节点的子节点即可。
• 第三种情况：要删除的节点有两个子节点，我们需要在删除节点的右子树中，寻找到最小的那个节点，然后将其放在删除的节点的位置上。

三种情况对应下图：

结合代码来理解一下：

    //3.删除数据
    public void delete(int value){
        Node p = head;
        Node pParent = null;//p节点的父节点

        //先找到这个节点
        while (p != null && p.getData() != value){
            pParent = p;
            if (p.getData() > value)p = p.left;
            else p = p.right;
        }
        if (p == null) return;//表示没有找到值为value的节点

        //1.假如要删除的节点有两个子节点
        if (p.left != null && p.right != null){
            //查找p节点的右子节点中的最小值
            Node minP = p.right;
            Node minPP = p;//minPP表示minP的父节点
            while (minP.left != null){
                minPP = minP;
                minP = minP.left;
            }
            p.data = minP.getData();
            if (minPP == p) p.right = null;
            else minPP.left = null;
            return;
        }

        //2.假如删除的节点p是叶子节点或只有一个子节点
        Node child = null;
        if (p.left != null) child = p.left;
        else if (p.right != null) child = p.right;

        if (pParent == null) head = child;
        else if (pParent.left == p) pParent.left = child;
        else pParent.right = child;
    }

5. 二叉搜索树分析

最后，还有两个需要说明一下，前面说到了二叉树的三种遍历方式，其中，中序遍历的方式是先遍历节点的左子节点，再遍历这个节点本身，然后遍历节点的右子节点。所以，如果中序遍历二叉搜索树，会得到一个有序的数据，时间复杂度是 O(n)，所以二叉搜索树又叫做二叉排序树。

在理想的情况下，我们的二叉树是一棵满二叉树或者完全二叉树，那么查找、插入、删除操作十分的高效，时间复杂度是 O(logn)，但是，如果二叉树的左右子树非常的不平衡，极端的情况下，可能会退化为链表，那么性能就下降了。

所以，我们需要一种方式来维持二叉树的平衡，最好是将其维持为满二叉树或者完全二叉树，这就是后面会说到的平衡二叉查找树，常见的有 AVL 树，红黑树。