跳表(skip list)
数组和链表对比:
- 数组支持随机访问,根据下标随机访问的时间复杂度是 O(1)
- 数组的插入和删除操作效率不高,平均情况下的时间复杂度是 O(logN)
- 链表随机访问性能没有数组好,平均情况下的时间复杂度是 O(logN)
- 链表插入和删除操作只需要改变相邻节点的指针,时间复杂度是 O(1)
二分查找底层依赖数组结构,跳表通过构建多级索引来提高查询效率,实现了基于链表结构的“二分查找”(查找、删除、添加等操作都可以拥有对数时间复杂度)
跳表时间和空间复杂度:
- 查询操作的平均时间复杂度是 O(logN),最坏时间复杂度 O(N)
- 插入操作的平均时间复杂度是 O(logN),最坏时间复杂度 O(N)
- 删除操作的平均时间复杂度是 O(logN),最坏时间复杂度 O(N)
- 平均空间复杂度是 O(N),最坏空间复杂度 O(N logN)
跳表时间复杂度分析:
- 设原始链表有 N 个节点,每两个节点抽取一个节点作为上一级索引节点,这样第 k 层索引有 N/(2^k)个节点
- 设共有 h 级索引,最高一级索引有 2 个节点,结合上面的分析知道 N/2^h = 2,所以 h + 1 = log2(N)
- 加上原始链表这一层,整个跳表的高度是 log2(N)
- 查找某个数据时若每层需比较 m 个节点,总的时间复杂度是 log2(m*N),可简化为 O(logN)(m 是个常数)
跳表索引动态更新:
- 往跳表中插入数据时会选择性的将这个数据同步插入部分索引层中
- 由随机函数来确定需要插入哪些索引层级,这样在可以避免在插入大量数据后跳表查询性能退化
Redis 有序集合(Sorted Set)
Reids 有序集合支持的核心操作有:插入数据、查找数据、删除数据、根据 score 按照区间查找数据
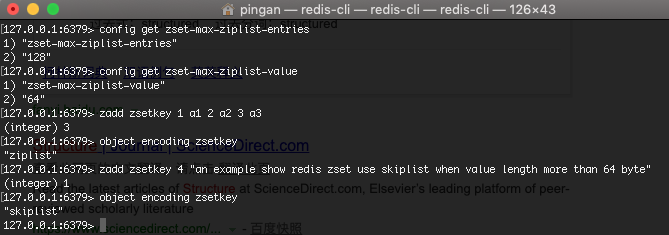
Redis 有序集合的底层编码有两种实现,分别是 ziplist 和 skiplist,当有序集合的元素个数小于 zset-max-ziplist-entries 配置(默认128个),并且每个元素的值都小于 zset-max-ziplist-value 配置(默认64字节)时,Redis 会用 ziplist 来作为有序集合的内部实现,上述两个条件之一不满足时,Redis 启用 skiplist 作为有序集合的内部实现(转换过程是不可逆转,只能从小内存编码向大内存编码转换)
下面演示了先查看 redis 的默认配置,并演示了往 zset 中添加元素时由于元素大于 64 字节,Redis 内部存储结构由开始的 ziplist 转变为一个 dict 加一个 skiplist (dict 用来查询数据到分数的对应关系,而 skiplist 用来根据分数查询数据)
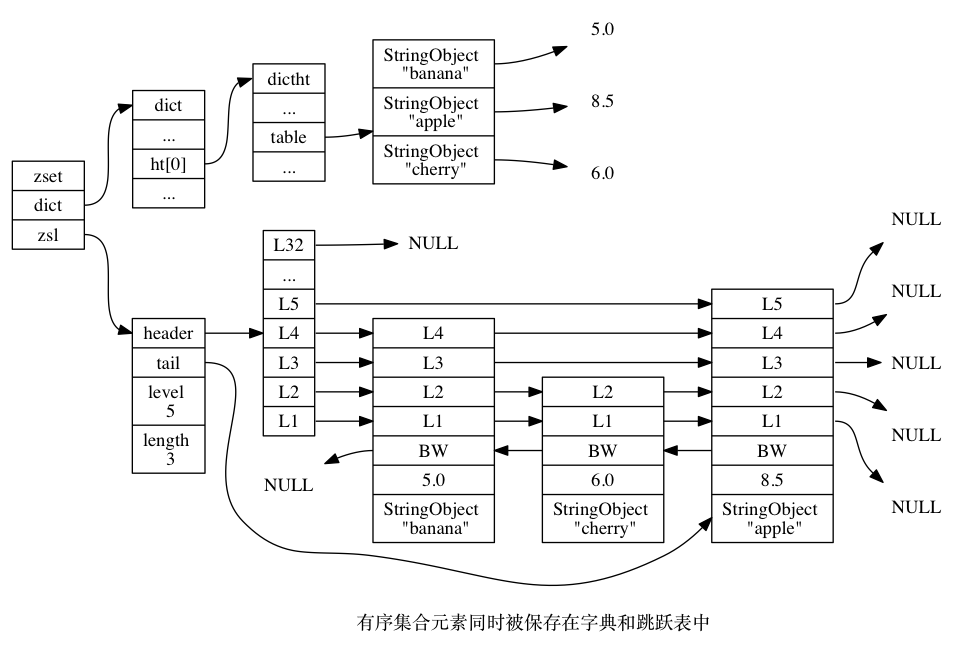
Redis 实现的跳跃表:
- Redis 的跳跃表实现由 zskiplist 和 zskiplistNode 两个结构组成, 其中 zskiplist 用于保存跳跃表信息(比如表头节点、表尾节点、长度), 而 zskiplistNode 则用于表示跳跃表节点
- 每个跳跃表节点的层高都是 1 至 32 之间的随机数(程序根据幂定律生成,越大的数出现的概率越小)
- 在同一个跳跃表中,多个节点可以包含相同的分值,但每个节点的成员对象必须是唯一的
- 跳跃表中的节点按照分值大小进行排序, 当分值相同时, 节点按照成员对象的大小进行排序
- 原始链表层的每个节点有一个指向前继节点的指针,用于从表尾方向向表头方向迭代(当执行 ZREVRANGE 或 ZREVRANGEBYSCORE 等逆序处理有序集的命令时用到)
为什么 Redis 用跳表而不是查找树实现有序集合:
- 针对数据插入、查询、删除及序区间查找等操作,跳表的时间复杂度不会比平衡树差
- 跳表比树的结构更简洁,这样代码更容易实现、更容易维护和调试
- 可以灵活的调整索引节点个数和原始链表节点个数之间的比例来平衡索引对内存的消耗和查询效率
有序结合使用字典结构的优势:
- 可以在 O(1) 时间复杂度内检查给定 member 是否存在于有序集
- 可以在 O(1) 时间复杂度内取出 member 对应的 score 值(实现 ZSCORE 命令)
为什么 Redis 使用 skiplist 转换 ziplist:
- 压缩列表是 Redis 为了节约内存而开发的, 由一系列特殊编码的连续内存块组成的顺序型(sequential)数据结构
- 压缩列表编码应用范围广泛,可以分别作为hash、list、zset类型的底层数据结构实现
- 压缩列表新增删除操作涉及内存重新分配或释放,加大了操作的复杂性,适合存储小对象和长度有限的数据
- Redis 提供了 {type}-max-ziplist-value 和 {type}-max-ziplist-entries 相关参数来控制 ziplist 编码转换
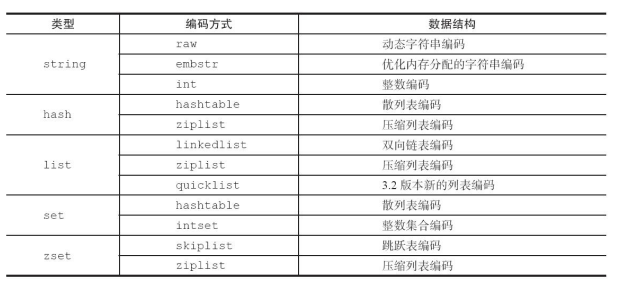
Redis 每种数据类型(type)可以采用的编码方式(encoding)对应关系
参考资料:
Redis Zset 源代码
Redis ZipList 源代码
Redis ziplist 设计与实现
Redis skiplist 设计与实现
Redis ziplist 实现有序集合
Redis skiplist 实现有序集合
Lucene 倒排索引列表
倒排索引/反向索引(Inverted index):
- 倒排索引用来存储在全文搜索下某个单词在一个文档或者一组文档中的存储位置的映射,如果把一本书的目录理解为书的正向索引,那么书最后的索引页就是书的倒排索引
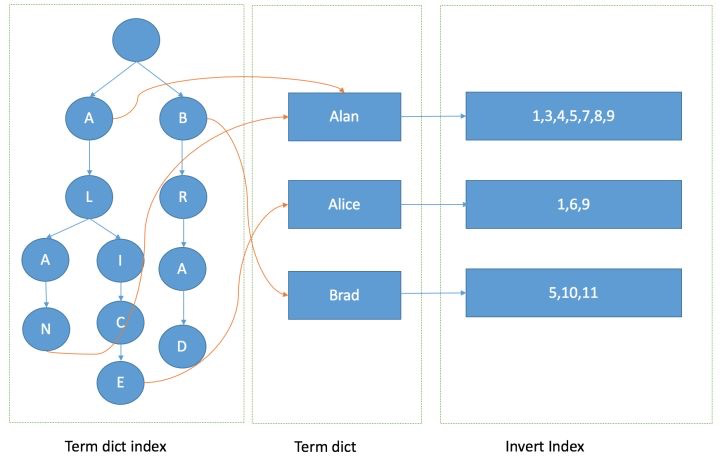
Lucene 是一个开源的高性能、可扩展的信息检索引擎,Lucene 的索引是基于倒排索引结构组织的,倒排列表本质上是基于 Term 的反向列表,倒排索引由 Term index,Term Dictionary 和 Posting List 组成
- 单词词典(Term Dictionary)记录所有文档的单词,并记录单词到倒排列表的关联关系
- 倒排列表(Posting list)记录了单词对应的文档集合,倒排链由有序的倒排索引项组成
- 倒排索引项(Posting)中包含了文档Id(docId)、词频(TF)、位置(Position)和偏移量(Offset)
为了能够快速进行倒排链的查找和 docid 查找,Lucene 倒排列表采用了 SkipList 结构,这样可以快速的对两个倒排列集合求交集和并集
Elasticsearch 搜索服务器底层依赖于 Lucene 检索引擎,Elasticsearch 在处理多个索引查询合并操作时支持 skip list、bitmap 和 Roaring bitmap 三种实现方式,如果查询的 filter 缓存到了内存中(以 bitset 的形式),那么合并就是两个 bitset 的 AND,如果查询的 filter 没有缓存就用 skip list 的方式去遍历两个 on disk 的 posting list
参考资料:
Multi-level skipping on posting lists
Frame of Reference and Roaring Bitmaps
MultiLevelSkipListWriter.java
MultiLevelSkipListReader.java
时间序列数据库的秘密——索引
Lucene 查询原理及解析
基于Lucene查询原理分析Elasticsearch的性能
B-树(B-Tree)
二叉查找树(binary search tree):
- 每个节点其左子树上所有节点值要小于该节点值,右子树上所有节点的值要大于该节点值
平衡二叉树查找树:
- 二叉树查找树中任意节点的左子树和右子树的高度差不大于一
B-Tree 遵循如下规则:
- B-Tree 是一种自平衡的 M 叉查找树
- 根节点至少存在两个子节点,至多存在 M 个子节点
- 除了根节点和叶子节点,每节点包含 k-1 个关键字和 k 个指向子节点的指针(k 的取值范围[M/2,M])
- 叶子节点包含 k-1 个关键字(k 的取值范围 [M/2,M] )
- 所有叶子节点在树的同一层
B+树(B+Tree)
B+ 树遵循如下规则:
- B+Tree 是一颗自平衡的查找树
- 每个节点最多有 M 个子节点(下文 MySQL 索引部分说明 M 取值)
- 除根节点外,每个节点至少有 M/2 个子节点,根节点至少有两个子节点
- 非叶子节点中只存储关键字和指向子节点的指针,不存储指向实际数据的指针
- 通过双向链表将叶子节点串联起来,可以方便按区间查找(不用每次返回根节点)
B+ 树时间和空间复杂度:
- 查询数据的时间复杂度是 O(logN)
- 插入操作的时间复杂度是 O(logN)
- 删除操作的时间复杂度是 O(logN)
- 空间复杂度是 O(N)
B+ 树动态更新索引节点:
- 写入数据后若某节点的子节点个数大于 M,会将对应节点分裂为两个节点,父节点如有需要会级联分裂
- 删除数据后,如某节点的子节点个数小于 M/2,将相邻的兄弟节点合并
B+Tree 与 B-Tree 不同点:
- 每个节点有 k 个关键字就有 k 个子节点(B-Tree 有 k 个关键字时有 k+1 个子节点)
- 非叶子节点的关键字也存在于子节点中,并且是子节点中的最小/最大关键字
- B+Tree 非叶子节点只用于索引,不保存数据记录(B-Tree 中非叶子节点既保存索引也保存数据记录)
- B+Tree 关键字只出现在叶子节点,并且构成有序链表(按关键字从小到大排列)
MySQL InnoDB 索引
文件系统和数据库系统通常使用 B+Tree 来存储索引,MySQL 的大部分索引(PRIMARY KEY、UNIQUE INDEX)使用 B+Tree 结构存储,也有一些特例,如 InnoDB 使用倒排索引(inverted lists)作为全文索引(FULLTEXT)的存储结构 (MongoDB 也是使用 b-tree 构造索引)
- MySQL 的索引分为聚簇索引(clustered index)和二级索引(secondary index)
- 可以把 MySQL 的索引理解为一颗聚簇索引 B+Tree 和其他一到多颗二级索引 B+Tree
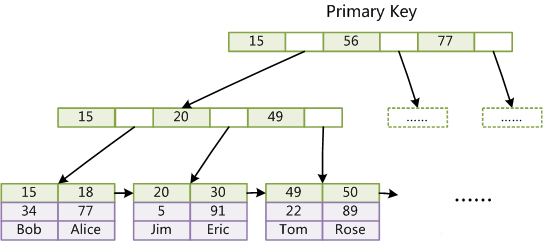
- 聚簇索引树的叶子节点保存了主键和实际数据记录行
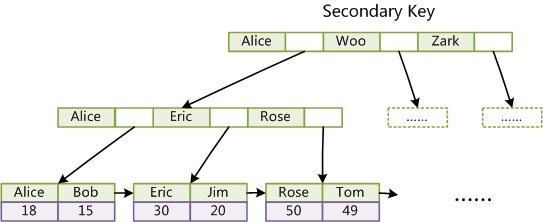
- 二级索引树的叶子节点保存了指向主键的指针和创建二级索引的列数据
聚簇索引:
二级索引:
MySQL 不同存储引擎支持的索引存储结构如下
为什么 MySQL 使用 B+Tree 结构实现索引:
- 对于数据存储在磁盘中的数据库系统而言,I/O 操作次数是影响性能的重要因素
- 操作系统是按页(getconf PAGESIZE,默认 4K)读取磁盘中数据,一次读取一页数据
- 如果读取的数据量超过一页大小,会触发多次 I/O 操作
- 若 M 的取值让每个节点大小等于页大小,这时读取一个节点只需要一次磁盘 I/O 操作
- B+Tree 的非叶子结点只保存关键字和指向子结点的指针,相同的页大小可以存储更多的节点数,同时减少了树的高度增加了树的分叉数,进而减少了磁盘 I/O 操作次数
- 删除数据时更简单,因为 B+Tree 实际数据只保存在叶子结点,所以不需要删除非叶子结点
为什么 MySQL InnoDB 索引遵循最左匹配原则
- InnoDB 存储引擎使用 B+Tree 保存索引
- B+Tree 是一颗所有节点有序的查找树,每次查找从根节点开始对比,根据比较的结果确定继续查找左子树或右子树
处理从右到左匹配的需求:
方案一:表结构新增一列用来存储需要从右到左匹配列的倒序字符并构建索引,缺点是新增列和索引都需要占用磁盘空间
方案二:Mysql 5.7 版本提供了虚拟列功能,使用 reverse 函数构建虚拟列并创建索引
具体脚本可以参考 mysql innodb 索引使用指南
参考资料:
create-index
https://dev.mysql.com/doc/internals/en/innodb-fil-header.html
高性能 mysql
mysql 5.7 virtual generated columns index
create-table-generated-columns
红黑树(Red-Black Tree)
红黑树是一颗自平衡的二叉查找树(只做到了近似平衡)
红黑树遵循如下规则:
- 每个节点要么是红色要么是黑色
- 根节点始终是黑色的
- 没有相邻的两个红色节点(每个红色节点的两个子节点都是黑色)
- 从任意节点到任意叶子节点的路径,包含相同数量的黑色节点
红黑树与 B+Tree 对比:
- B+Tree 比红黑树的查询性能更好,因为 B+Tree 是严格的平衡树
- 红黑树比 B+Tree 的插入和删除性能更好(红黑树有更松散的平衡性,插入和删除数据后树的节点再平衡操作更少,性能更稳定)
- 红黑树适合用于构建存储在内存中的索引如 JDK 中 HashMap,B+Tree 适合用来构建存储在磁盘中的索引,如 MySQL 和 Oracle 中的索引
JDK HashMap
Java 7 以及之前版本的 HashMap 同一个桶(Bucket)里面的节点(Entry)使用链表(Linked list)串联起来,当同一个桶里面存在过多节点时(对不同 key 的 hashcode 函数取值相等),查询时间的复杂度会从哈希 O(1) 退化到链表 O(N),为了避免上述问题, Java 8 的 HashMap 同一个桶中的节点个数在满足一定条件时会使用红黑树结构代替链表结构
红黑树和链表相互转换规则:
- 当单个桶中的节点个数大于 TREEIFY_THRESHOLD( 默认 8),并且桶的个数大于 MIN_TREEIFY_CAPACITY( 默认 64),对应的桶会使用红黑树替代链表结构
- 当移除元素后单个桶中的节点个数小于 UNTREEIFY_THRESHOLD( 默认 6),对应的桶会从红黑树恢复到链表结构
/**
* The bin count threshold for using a tree rather than list for a bin.
* Bins are converted to trees when adding an element to a bin with at least this many
* nodes The value must be greater than 2 and should be at least 8 to mesh with
* assumptions in tree removal about conversion back to plain bins upon shrinkage.
*/
static final int TREEIFY_THRESHOLD = 8;
/**
* The bin count threshold for untreeifying a bin during a resize operation.Should be less
* than TREEIFY_THRESHOLD, and at most 6 to mesh with shrinkage detection under removal.
*/
static final int UNTREEIFY_THRESHOLD = 6;
/**
* The smallest table capacity for which bins may be treeified. (Otherwise the table is
* resized if too many nodes in a bin.) Should be at least 4 plus TREEIFY_THRESHOLD to
* avoid conflicts between resizing and treeification thresholds.
*/
static final int MIN_TREEIFY_CAPACITY = 64;JDK ConcurrentSkipListMap
- ConcurrentSkiplistMap 对插入,删除,更新和获取元素支持并发操作
- map 的元素根据创建时 key 的自然顺序排序
- 针对 containsKey、get、put 和 remove 操作确保了 O(log(n)) 的平均时间复杂度
- ConcurrentSkiplistMap 是基于 skiplist 结构实现的
/**
* A scalable concurrent ConcurrentNavigableMap implementation.The map is sorted
* according to the {@linkplain Comparable natural ordering} of its keys, or by a
* Comparator provided at map creation time, depending on which constructor is used.
*
* <p>This class implements a concurrent variant of SkipLists providing expected
* average <i>log(n)</i> time cost for the {@code containsKey}, {@code get},
* {@code put} and {@code remove} operations and their variants. Insertion, removal,
* update, and access operations safely execute concurrently by multiple threads.
*/JDK TreeMap 与 TreeSet
- JDK TreeMap 是基于红黑树实现了 java.util.NavigableMap 接口
- TreeMap 的元素根据创建时 key 的自然顺序排序
- TreeMap 提供了在 log(N) 平均时间复杂度下的 get,put,containsKey 和 remove 操作
/**
* A Red-Black tree based {@link NavigableMap} implementation. The map is sorted according
* to the {@linkplain Comparable natural ordering} of its keys, or by a {@link Comparator}
* provided at map creation time, depending on which constructor is used.
*
* This implementation provides guaranteed log(n) time cost for the {@code containsKey},
* {@code get}, {@code put} and {@code remove} operations. Algorithms are adaptations of
* those in Cormen, Leiserson, and Rivest's Introduction to Algorithms.
*/- JDK TreeSet 是基于 TreeMap 实现了 java.util.NavigableSet 接口
- TreeSet 的元素根据创建时 key 的自然顺序排序
- TreeSet 提供了在 log(N) 平均时间复杂度下的 add,remove 和 contains 操作
/**
* A {@link NavigableSet} implementation based on a {@link TreeMap}.
* The elements are ordered using their {@linkplain Comparable natural
* ordering}, or by a {@link Comparator} provided at set creation
* time, depending on which constructor is used.
*
* <p>This implementation provides guaranteed log(n) time cost for the basic
* operations ({@code add}, {@code remove} and {@code contains}).
*/





**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。