本篇其实主要想讲数据结构的,但是结合上篇的时间复杂度来说的话,本篇我觉得写一些基本的排序算法,进而分析它的复杂度会好一些。
概览
如果你经常刷一些算法题,可能会发现,百分之80以上的题都会用到排序。并且,也可能你学习算法时第一个遇到的就是排序了!排序非常重要,可以说掌握了复杂度分析加一些基本的排序,去处理一些前端的大量数据操作问题都会变得容易起来。当然,如果你再掌握了一些基本的数据结构就更好不过了。
不过呢,排序算法真的是太多了,很可能一些连名字都没听说过,比如猴子排序、睡眠排序、鸡尾酒排序、鸽巢排序、面条排序以及一些不实用的Bogo排序、珠排序等。所以这里只讲一下众多排序算法中的一小部分,也是最基本的、最实用的:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。
介绍
说到算法,就要说这个算法的优缺点,排序算法也不例外,我们一般会从这几方面分析一个排序算法:
1、执行效率 2、稳定性 3、内存消耗
首先说执行效率
如果你看了我的上一篇文章复杂度分析
应该会有所想法,说白了就是分析这个排序算法的最好、最坏以及平均时间复杂度。 进一步优化我们还会继续分析时间复杂度的系数、常数 、低阶,因为O(logn)的排序就不一定比O(n^3)好,因为我知道在n无穷大的时候logn << n^2,但是有时候你排序的数据可能开始你就能确定n的范围,比如n <= 1000,那么1000000logn就不如2n^2,当然我只是举个例子说明一下
稳定性
排序算法的稳定性是什么呢?简单说一下就是如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。举个例子
11, 2, 5, 19, 100, 2,小到大排序完之后应该是2,2,5,11,19,100.我们可以看到这组数据中有两个2,也就是说如果排序完之后两个2的相对顺序不变,那么这个排序算法就是稳定排序算法,反之为不稳定排序算法。有人会问这两个2谁先谁后有关系吗?那好,我再写一个明确点的例子:
{sing_price: 4, total_price: 1000}, {sing_price: 2, total_price: 600}, {sing_price: 2, total_price: 1200}, {sing_price: 20, total_price: 40}.
有所感悟了吧?因为我们开发的时候大多数都是面向对象来进行程序设计,这个时候稳定排序算法的优势就体现出来了。比如我上面的例子是一个商品的列表,我们要求按照单价排序,如果相等那么再按照总价排序,假设我们有100万个商品。那么我们有两种方法可以实现。
一是先按照单价进行一遍排序,然后再找出相等单价的商品再按照总价继续排序,这种算法上实现起来会有困难,因为我们还要找出或者储存有相等单价的商品。
二是借助稳定排序算法的特点,我们先按照商品的单价排序之后,再按照总价排序一遍就实现了,中间我们是可以加入一些flag来优化的,实现起来很容易,算法也可以复用。
内存消耗
上篇讲过,内存消耗可以用空间复杂度来表示,在排序算法里还有一个概念就是原地排序算法,意思就是不需要借助额外的内存空间来进行排序(即空间复杂度O(1))。
下面开始讲一些基本地排序算法
正题
冒泡排序
这个名字很有意思,冒泡排序?
因为冒泡排序每次会操作相邻的两个数据。比较他们两个的大小是否满足我们的约定,如果不满足,那么就将两个数据交换顺序,所以每次操作都会确定当前操作的两个数据的正确位置,对于n的数据,我们操作n次就完成了n个数据的排序工作,也就是冒泡排序就是元素不断交换的过程。
用一张形象图比喻一下,比如我们是从小到大排序,那么,每次比较的过程中,较大的数据一定会向后移,小的气泡想上冒,大的气泡像后移,第一次遍历之后,最大的气泡就一定再最后的位置,然后我们就来比较剩下的n-1就好了,依次类推,最后完成冒泡。过程:
代码实现:
function sort(arr) {
let l = arr.length;
let i = 0;
while (i !== l) {
let j = 0;
while (j !== l - i - 1) {
if (arr[j] > arr[j + 1]) {
let cache = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = cache
}
j++
}
i++
}
}
上面的代码可以改进一下,就是在某次排序的的时候(在第二层while循环里),若整个循环没有发生数据交换,那么说明该组数据已经完全有序,可以直接return;方法就是声明一个是否发生交换的标志flag = false,当有数据交换的时候我们置为true,若循环完之后flag仍为false,则可以退出循环,否则重置为false,进入下一个while循环。
我们在优化版的冒泡排序中分析复杂度。
首先最好时间复杂度 -> 1, 2, 3, 4, 5 复杂度为O(n)
最坏时间复杂度 5,4,3,2,1。 复杂度为O(n^2)
这两个很简单,就不多做分析。那么平均时间复杂度呢?
我在上篇文章说过平均时间复杂度就是加权平均期望时间复杂度。冒泡排序我先细致地分析一下如何计算,后面的就不再一一地分析了。
这种优化后的冒泡排序如果用概率的分析方法非常复杂,我们可以换个角度想问题,其实排序实际上就是将无序变为了有序,所以这里我们引入两个新概念:有序度,逆序度
有序度
有序度是数组中具有有序关系的元素对的个数,即如果j < k, 则a[j] <= a[k]。举个例子 5,4,1,3,2,6的有序度为6,即(1,3),(1,2),(2,6),(3,6),(4,6),(5,6)。特殊的,像5,4,3,2,1的有序度即为0.
1,2,3,4,5 这里我们随意取两个数均为有序,若1,2,3,...n呢?那就是我们在n中任意选择两个数均是有序,那么就是Cn2, 即n (n-1)/2 1 = n(n-1)/2,像这种情况我们称之为满有序度。
逆序度
这个不用写了吧?想必大家都已经猜出,逆序度 + 有序度 = 满有序度
那么我们回到题中去分析。我们知道如果当发生交换时,即这个操作执行时:
if (arr[j] > arr[j + 1]) {
let cache = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = cache
}就发生了一次 有序度 + 1, 逆序度 - 1的事情。像 5,4,1,3,2,6 的初始有序度为6,满有序度为15,那么一定会发生15 - 6 = 9次交换才能排序完成。如果是n个数据呢?那么最好情况是0次交换,最坏是n(n-1)/2.那么平均情况就是n(n-1)/4次交换。注意,这里只是交换,比较操作是每次都会进行的。但是最坏也只是n(n-1)(n-2)...21 <= n^2。所以我们可以说平均情况下的时间复杂度就是O(n^2).虽然不严格,但是比起我们用概率和期望的方法去定量分析会容易太多!
鸡尾酒排序
这个排序用的不多,其实就是双端冒泡,即第一次若找出最大值放后面,下一轮则找出最小值放前面。例 3, 1, 4, 9, 5。经过第一次排序我们将9放到了最后面 第二次我们找到了最小值1放到最前面,依次轮换。知道完全排好为止,了解一下即可。
插入排序
在说插入排序之前,我先说一个场景,排队的时候,假设已经都按大小身高排好了,这时候又新加入一名同学,那么该怎么办呢?很明显他可以从头开始比较,遇到比自己矮的就再往后找,直到找到第一个比自己高的为止,然后站在他的前边。图:
从图中来讲,假设要排序的是一个数组,那么我们可以分成两个部分,一是已经排序好的部分,二是未排好的部分。或者三个部分的话就多了一个正要插入的元素。总之,思路是一样的。当未排好的部分元素长度为0时说明数组整体完全有序,排序算法完成,初始的时候,已排好的区间只有一个元素,图中来讲就是3,每次从未排好区间取一个元素,插入到已排好区间,依次从后往前比较,若满足条件则直接插入到当前位置,否则,被比较的元素向后移动一个位置(腾地),继续比较。代码实现(从小到大排列)
function sort(arr) {
let l = arr.length;
// 因为第一个元素我们已经假定是排好的,所以i从1开始取
let i = 1, j
for ( ; i < l; i++) {
let target = arr[i]
let j = i - 1
for (; j >= 0; j--) {
//如果选中的元素大于前一个元素,证明已经排好
if (target > arr[j]) {
break;
} else {
// 否则前一元素向后移,为目标元素留出位置
arr[j + 1] = arr[j]
}
}
// 最后在空位置插入
arr[j + 1] = target;
}
}动态演示
分析:
首先插入排序是稳定排序算法吗?
我们在代码中可以看出,对于相等的两个元素,我们没有交换位置而是认定为此元素排序完成(即找到了该插入的位置),所以插入排序是稳定排序算法
插入排序是原地排序吗?
从始至终我们没有申请额外的存储空间,所以插入排序是原地排序算法
插入排序的时间复杂度是多少?
首先,最好时间复杂度(初始即有序),那么每次我们只比较一次就可以确定位置,一共n次即可完全有序,复杂度O(n)
最坏情况时间复杂度(初始完全逆序),那么每次都要比较当前下标前的所有元素,即共需 1 + 2 + ... + n = (n + 1)n / 2。
那么平均情况呢?
我们还用有序度来分析,假设满有序度为20,初始为5,当我们进行位移比较的时候,每位移一次,逆序度-1,有序度+1.同冒泡排序分析可得平均时间复杂度也是O(n^2)
选择排序
选择排序,顾名思义,每次都都针对性的选择排序,即每次选出最小值放在最前面或者最大值放在最后面。图:
直接上代码:
function sort(arr) {
let l = arr.length;
let minIndex = 0;
for (let i = 0; i < l; i++) {
for (let j = i; j < l; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j
}
}
let cache = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = cache;
}
}
分析:
因为这种算法的复杂度计算非常稳定,都是O(n^2),所以复杂度这里就不再啰嗦。
分析一下选择排序算法是否稳定,我们给一个例子 9, 15, 12, 9 , 0.
显然第一次选择的时候我们筛选出0是最小的,所以和第一个9交换,那么原有的两个9的相对顺序已经改变。所以,选择排序是一种不稳定地排序算法。但因为理解起来相对容易,所以在数据规模不大的情况下以及对相同元素的没有要求的情况下,还是可以使用的。冒泡排序与插入排序相比,最好、最坏以及平均时间复杂度上看起来差不多。但是,这种情况下,我们往往会比较低阶,以及系数。假设逆序度相同的情况下,那么从逆序变成完全有序的次数也就是相同的,但是冒泡排序的交换操作需要三步:
cache = a[j];a[j] = a[j + 1];a[j+1]=cache。
而插入排序则只需要一步arr[j - 1] = target即可;
(选看)插入排序进阶-->插半排序
我们上面实现的算法是直接插入排序,即每次都从未排好区间取一个元素,与前面已排好区间从后往前依次比较。如果数据量很大的时候,已排好区间元素越多,我们可能遍历的次数就越多,打个比方
18, 52, 66, 11.......{10000个}...... 999, 1
当我们排最后一个元素1的时候,需要将插入指针从已排好区间的末尾一直走到最前面,在大数据量的情况下不是很高。
其实我们知道了已排好区间的数据是有序的,那么我们就可以用二分比较的方法。
例如 5, 7, 8, 10, 12, 16, 18, 19,22为已排好区间。 我们这时候从未排好区间拿出一个数,假如为9, 那么先直接与已排好区间arr[(0 + i)/2]比较,也就是12, 9 < 12,说明要在5 - 10这个区间 ,即arr[0 - (0 + i)/2]中继续比较。直到找到位置后插入。这样我们每次都缩小了一半的查找范围,实现起来不是很难,大家有时间可以自己实现一下。
希尔排序
其实这个排序算法我是想放到下一篇文章来写的,因为我们可以发现,上面所有算法的平均时间复杂度都是O(n^2),对于大数据量的数据处理还是显得性能低下,下一篇会讲的是O(nlogn)的排序算法,而希尔排序的平均时间复杂度也是O(nlogn),但由于它是插入的优化版,里面有我下一篇文章将要讲得分治思想。
为什么说希尔排序是插入排序的优化版呢?因为它解决了影响插入排序效率最重要的一个特点 插入排序每次只能将数据移动一位
为什么说这个影响了效率? 请看上面插半排序。刚才说过如果最后一位恰巧是最小的(假设从小到大排列),那么意味着这个最小的元素要一位一位地向前移动!而希尔排序的主要特点:
- 先将带排序区间按照某一间隔划分为若干个小区间
- 对每个小区间进行插入排序
- 再次缩小间隔直至为1,再次进行插入排序
1和3可以合并为1类。总得来说就是每次划分并排序之后,该整体区间的有序度就提高,即每次缩小间隔之后,我们再次进行排序的有序度整体提升,这句话需要好好理解一下。我先用图来表达一下:
首先我们要排序的一组数据是
9,2,12,28,44,56,7,8,14,3,15,1
我们第一次取步长间隔为 数据长度/2,之后再次除2,直到为1为止。可以看到最小的元素很快地就已经确定好位置,并且排在了前面,同时我们的最后一次排序也是在高度有序的基础上进行插排。代码实现
function sort(arr) {
let l = arr.length;
for (let step = l >> 1; step > 0; step >>= 1) {
for (let i = step; i < l ; i++) {
let target = arr[i];
let j = i - step;;
for (; j >= 0 && target <= arr[j] ; j -= step ) {
/**
* 搬移数据,注意这里要加上步长,这个地方不太好理解,你可以空间想象一下,我们并不是顺序比较
* 要想象出把同步长的下标元素分离出来比较
*/
arr[j + step] = arr[j]
}
arr[j + step] = target
}
}
}
进行分析
1、希尔排序是原地算法吗? 是
2、希尔排序是稳定算法吗? 不是
其实很容易想到,因为我们分了区间进行排序,所以就很可能导致相同的元素发生位置的相对顺序改变。举个最简单的例子
7,2(a),2(b),1
开始 7, 2(b)排序, 2(a),1排序
第一次结果 2(b),1,7,2(a)
可以发现两个2的相对改变。
3、希尔排序的时间复杂度是多少?
最好:O(n log n)。
最坏:O(n log n)。
平均:O(n log n)。
由于时间有些紧,所以有些地方可能有错别字,并且代码实现也不一定是最简单,最佳的,还请大家多多包涵,下一篇会介绍一些复杂度为nlogn的排序算法。大家加油!

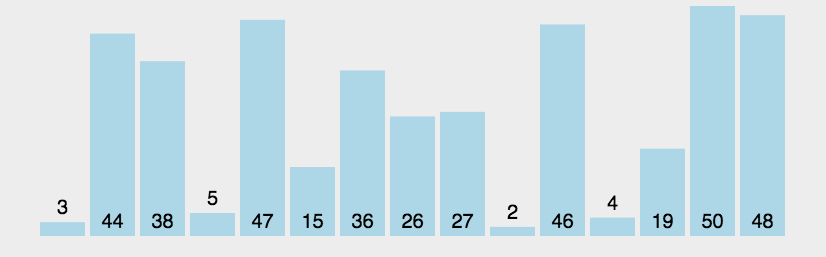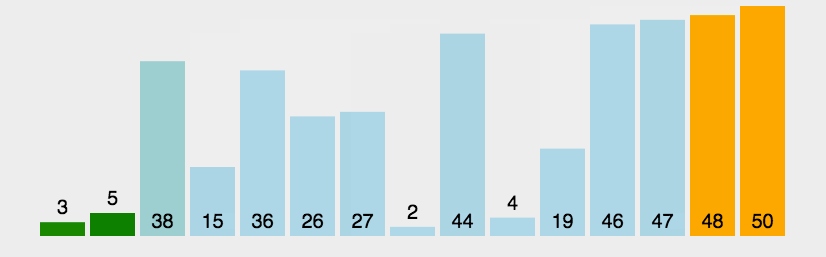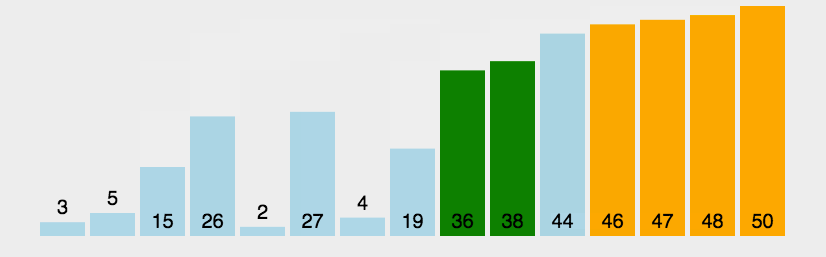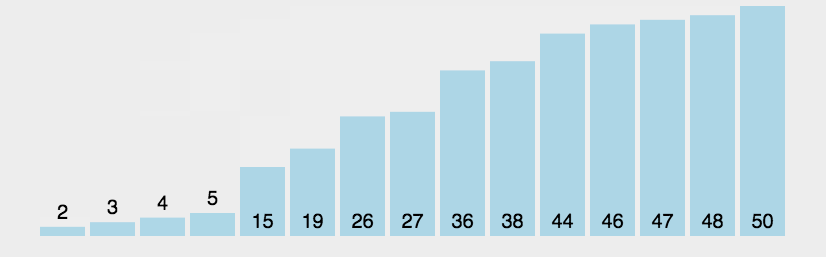




**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。