在搜索领域,早已出现了“查找相似图片/相似商品”的相关功能,如 Google 搜图,百度搜图,淘宝的拍照搜商品等。要实现类似的计算图片相似度的功能,除了使用听起来高大上的“人工智能”以外,其实通过 js 和几种简单的算法,也能八九不离十地实现类似的效果。
在阅读本文之前,强烈建议先阅读完阮一峰于多年所撰写的《相似图片搜索的原理》相关文章,本文所涉及的算法也来源于其中。
特征提取算法
为了便于理解,每种算法都会经过“特征提取”和“特征比对”两个步骤进行。接下来将着重对每种算法的“特征提取”步骤进行详细解读,而“特征比对”则单独进行阐述。
平均哈希算法
参考阮大的文章,“平均哈希算法”主要由以下几步组成:
第一步,缩小尺寸为8×8,以去除图片的细节,只保留结构、明暗等基本信息,摒弃不同尺寸、比例带来的图片差异。第二步,简化色彩。将缩小后的图片转为灰度图像。
第三步,计算平均值。计算所有像素的灰度平均值。
第四步,比较像素的灰度。将64个像素的灰度,与平均值进行比较。大于或等于平均值,记为1;小于平均值,记为0。
第五步,计算哈希值。将上一步的比较结果,组合在一起,就构成了一个64位的整数,这就是这张图片的指纹。
第六步,计算哈希值的差异,得出相似度(汉明距离或者余弦值)。
明白了“平均哈希算法”的原理及步骤以后,就可以开始编码工作了。为了让代码可读性更高,本文的所有例子我都将使用 typescript 来实现。
图片压缩:
我们采用 canvas 的 drawImage() 方法实现图片压缩,后使用 getImageData() 方法获取 ImageData 对象。
export function compressImg (imgSrc: string, imgWidth: number = 8): Promise<ImageData> {
return new Promise((resolve, reject) => {
if (!imgSrc) {
reject('imgSrc can not be empty!')
}
const canvas = document.createElement('canvas')
const ctx = canvas.getContext('2d')
const img = new Image()
img.crossOrigin = 'Anonymous'
img.onload = function () {
canvas.width = imgWidth
canvas.height = imgWidth
ctx?.drawImage(img, 0, 0, imgWidth, imgWidth)
const data = ctx?.getImageData(0, 0, imgWidth, imgWidth) as ImageData
resolve(data)
}
img.src = imgSrc
})
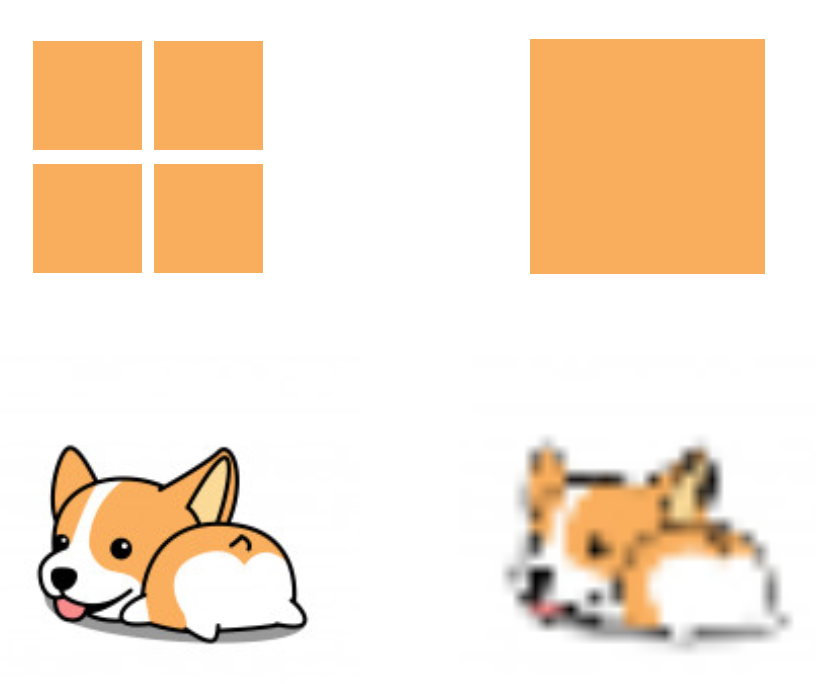
}可能有读者会问,为什么使用 canvas 可以实现图片压缩呢?简单来说,为了把“大图片”绘制到“小画布”上,一些相邻且颜色相近的像素往往会被删减掉,从而有效减少了图片的信息量,因此能够实现压缩的效果:
在上面的 compressImg() 函数中,我们利用 new Image() 加载图片,然后设定一个预设的图片宽高值让图片压缩到指定的大小,最后获取到压缩后的图片的 ImageData 数据——这也意味着我们能获取到图片的每一个像素的信息。
关于 ImageData,可以参考 MDN 的文档介绍。
图片灰度化
为了把彩色的图片转化成灰度图,我们首先要明白“灰度图”的概念。在维基百科里是这么描述灰度图像的:
在计算机领域中,灰度(Gray scale)数字图像是每个像素只有一个采样颜色的图像。
大部分情况下,任何的颜色都可以通过三种颜色通道(R, G, B)的亮度以及一个色彩空间(A)来组成,而一个像素只显示一种颜色,因此可以得到“像素 => RGBA”的对应关系。而“每个像素只有一个采样颜色”,则意味着组成这个像素的三原色通道亮度相等,因此只需要算出 RGB 的平均值即可:
// 根据 RGBA 数组生成 ImageData
export function createImgData (dataDetail: number[]) {
const canvas = document.createElement('canvas')
const ctx = canvas.getContext('2d')
const imgWidth = Math.sqrt(dataDetail.length / 4)
const newImageData = ctx?.createImageData(imgWidth, imgWidth) as ImageData
for (let i = 0; i < dataDetail.length; i += 4) {
let R = dataDetail[i]
let G = dataDetail[i + 1]
let B = dataDetail[i + 2]
let Alpha = dataDetail[i + 3]
newImageData.data[i] = R
newImageData.data[i + 1] = G
newImageData.data[i + 2] = B
newImageData.data[i + 3] = Alpha
}
return newImageData
}
export function createGrayscale (imgData: ImageData) {
const newData: number[] = Array(imgData.data.length)
newData.fill(0)
imgData.data.forEach((_data, index) => {
if ((index + 1) % 4 === 0) {
const R = imgData.data[index - 3]
const G = imgData.data[index - 2]
const B = imgData.data[index - 1]
const gray = ~~((R + G + B) / 3)
newData[index - 3] = gray
newData[index - 2] = gray
newData[index - 1] = gray
newData[index] = 255 // Alpha 值固定为255
}
})
return createImgData(newData)
}ImageData.data 是一个 Uint8ClampedArray 数组,可以理解为“RGBA数组”,数组中的每个数字取值为0~255,每4个数字为一组,表示一个像素的 RGBA 值。由于ImageData 为只读对象,所以要另外写一个 creaetImageData() 方法,利用 context.createImageData() 来创建新的 ImageData 对象。
拿到灰度图像以后,就可以进行指纹提取的操作了。
指纹提取
在“平均哈希算法”中,若灰度图的某个像素的灰度值大于平均值,则视为1,否则为0。把这部分信息组合起来就是图片的指纹。由于我们已经拿到了灰度图的 ImageData 对象,要提取指纹也就变得很容易了:
export function getHashFingerprint (imgData: ImageData) {
const grayList = imgData.data.reduce((pre: number[], cur, index) => {
if ((index + 1) % 4 === 0) {
pre.push(imgData.data[index - 1])
}
return pre
}, [])
const length = grayList.length
const grayAverage = grayList.reduce((pre, next) => (pre + next), 0) / length
return grayList.map(gray => (gray >= grayAverage ? 1 : 0)).join('')
}通过上述一连串的步骤,我们便可以通过“平均哈希算法”获取到一张图片的指纹信息(示例是大小为8×8的灰度图):
感知哈希算法
关于“感知哈希算法”的详细介绍,可以参考这篇文章:《基于感知哈希算法的视觉目标跟踪》。
简单来说,该算法经过离散余弦变换以后,把图像从像素域转化到了频率域,而携带了有效信息的低频成分会集中在 DCT 矩阵的左上角,因此我们可以利用这个特性提取图片的特征。
该算法的步骤如下:
- 缩小尺寸:pHash以小图片开始,但图片大于88,3232是最好的。这样做的目的是简化了DCT的计算,而不是减小频率。
- 简化色彩:将图片转化成灰度图像,进一步简化计算量。
- 计算DCT:计算图片的DCT变换,得到32*32的DCT系数矩阵。
- 缩小DCT:虽然DCT的结果是3232大小的矩阵,但我们只要保留左上角的88的矩阵,这部分呈现了图片中的最低频率。
- 计算平均值:如同均值哈希一样,计算DCT的均值。
- 计算hash值:这是最主要的一步,根据8*8的DCT矩阵,设置0或1的64位的hash值,大于等于DCT均值的设为”1”,小于DCT均值的设为“0”。组合在一起,就构成了一个64位的整数,这就是这张图片的指纹。
回到代码中,首先添加一个 DCT 方法:
function memoizeCosines (N: number, cosMap: any) {
cosMap = cosMap || {}
cosMap[N] = new Array(N * N)
let PI_N = Math.PI / N
for (let k = 0; k < N; k++) {
for (let n = 0; n < N; n++) {
cosMap[N][n + (k * N)] = Math.cos(PI_N * (n + 0.5) * k)
}
}
return cosMap
}
function dct (signal: number[], scale: number = 2) {
let L = signal.length
let cosMap: any = null
if (!cosMap || !cosMap[L]) {
cosMap = memoizeCosines(L, cosMap)
}
let coefficients = signal.map(function () { return 0 })
return coefficients.map(function (_, ix) {
return scale * signal.reduce(function (prev, cur, index) {
return prev + (cur * cosMap[L][index + (ix * L)])
}, 0)
})
}然后添加两个矩阵处理方法,分别是把经过 DCT 方法生成的一维数组升维成二维数组(矩阵),以及从矩阵中获取其“左上角”内容。
// 一维数组升维
function createMatrix (arr: number[]) {
const length = arr.length
const matrixWidth = Math.sqrt(length)
const matrix = []
for (let i = 0; i < matrixWidth; i++) {
const _temp = arr.slice(i * matrixWidth, i * matrixWidth + matrixWidth)
matrix.push(_temp)
}
return matrix
}
// 从矩阵中获取其“左上角”大小为 range × range 的内容
function getMatrixRange (matrix: number[][], range: number = 1) {
const rangeMatrix = []
for (let i = 0; i < range; i++) {
for (let j = 0; j < range; j++) {
rangeMatrix.push(matrix[i][j])
}
}
return rangeMatrix
}复用之前在“平均哈希算法”中所写的灰度图转化函数createGrayscale(),我们可以获取“感知哈希算法”的特征值:
export function getPHashFingerprint (imgData: ImageData) {
const dctData = dct(imgData.data as any)
const dctMatrix = createMatrix(dctData)
const rangeMatrix = getMatrixRange(dctMatrix, dctMatrix.length / 8)
const rangeAve = rangeMatrix.reduce((pre, cur) => pre + cur, 0) / rangeMatrix.length
return rangeMatrix.map(val => (val >= rangeAve ? 1 : 0)).join('')
}颜色分布法
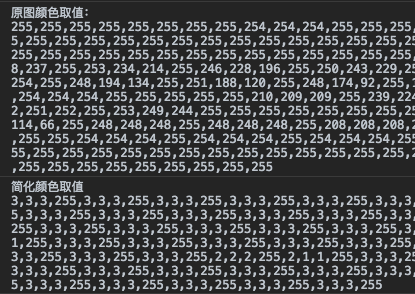
首先摘抄一段阮大关于“颜色分布法“的描述:
阮大把256种颜色取值简化成了4种。基于这个原理,我们在进行颜色分布法的算法设计时,可以把这个区间的划分设置为可修改的,唯一的要求就是区间的数量必须能够被256整除。算法如下:
// 划分颜色区间,默认区间数目为4个
// 把256种颜色取值简化为4种
export function simplifyColorData (imgData: ImageData, zoneAmount: number = 4) {
const colorZoneDataList: number[] = []
const zoneStep = 256 / zoneAmount
const zoneBorder = [0] // 区间边界
for (let i = 1; i <= zoneAmount; i++) {
zoneBorder.push(zoneStep * i - 1)
}
imgData.data.forEach((data, index) => {
if ((index + 1) % 4 !== 0) {
for (let i = 0; i < zoneBorder.length; i++) {
if (data > zoneBorder[i] && data <= zoneBorder[i + 1]) {
data = i
}
}
}
colorZoneDataList.push(data)
})
return colorZoneDataList
}把颜色取值进行简化以后,就可以把它们归类到不同的分组里面去:
export function seperateListToColorZone (simplifiedDataList: number[]) {
const zonedList: string[] = []
let tempZone: number[] = []
simplifiedDataList.forEach((data, index) => {
if ((index + 1) % 4 !== 0) {
tempZone.push(data)
} else {
zonedList.push(JSON.stringify(tempZone))
tempZone = []
}
})
return zonedList
}最后只需要统计每个相同的分组的总数即可:
export function getFingerprint (zonedList: string[], zoneAmount: number = 16) {
const colorSeperateMap: {
[key: string]: number
} = {}
for (let i = 0; i < zoneAmount; i++) {
for (let j = 0; j < zoneAmount; j++) {
for (let k = 0; k < zoneAmount; k++) {
colorSeperateMap[JSON.stringify([i, j, k])] = 0
}
}
}
zonedList.forEach(zone => {
colorSeperateMap[zone]++
})
return Object.values(colorSeperateMap)
}内容特征法
”内容特征法“是指把图片转化为灰度图后再转化为”二值图“,然后根据像素的取值(黑或白)形成指纹后进行比对的方法。这种算法的核心是找到一个“阈值”去生成二值图。
对于生成灰度图,有别于在“平均哈希算法”中提到的取 RGB 均值的办法,在这里我们使用加权的方式去实现。为什么要这么做呢?这里涉及到颜色学的一些概念。
具体可以参考这篇《Grayscale to RGB Conversion》,下面简单梳理一下。
采用 RGB 均值的灰度图是最简单的一种办法,但是它忽略了红、绿、蓝三种颜色的波长以及对整体图像的影响。以下面图为示例,如果直接取得 RGB 的均值作为灰度,那么处理后的灰度图整体来说会偏暗,对后续生成二值图会产生较大的干扰。
那么怎么改善这种情况呢?答案就是为 RGB 三种颜色添加不同的权重。鉴于红光有着更长的波长,而绿光波长更短且对视觉的刺激相对更小,所以我们要有意地减小红光的权重而提升绿光的权重。经过统计,比较好的权重配比是 R:G:B = 0.299:0.587:0.114。
于是我们可以得到灰度处理函数:
enum GrayscaleWeight {
R = .299,
G = .587,
B = .114
}
function toGray (imgData: ImageData) {
const grayData = []
const data = imgData.data
for (let i = 0; i < data.length; i += 4) {
const gray = ~~(data[i] * GrayscaleWeight.R + data[i + 1] * GrayscaleWeight.G + data[i + 2] * GrayscaleWeight.B)
data[i] = data[i + 1] = data[i + 2] = gray
grayData.push(gray)
}
return grayData
}上述函数返回一个 grayData 数组,里面每个元素代表一个像素的灰度值(因为 RBG 取值相同,所以只需要一个值即可)。接下来则使用“大津法”(Otsu's method)去计算二值图的阈值。关于“大津法”,阮大的文章已经说得很详细,在这里就不展开了。我在这个地方找到了“大津法”的 Java 实现,后来稍作修改,把它改为了 js 版本:
/ OTSU algorithm
// rewrite from http://www.labbookpages.co.uk/software/imgProc/otsuThreshold.html
export function OTSUAlgorithm (imgData: ImageData) {
const grayData = toGray(imgData)
let ptr = 0
let histData = Array(256).fill(0)
let total = grayData.length
while (ptr < total) {
let h = 0xFF & grayData[ptr++]
histData[h]++
}
let sum = 0
for (let i = 0; i < 256; i++) {
sum += i * histData[i]
}
let wB = 0
let wF = 0
let sumB = 0
let varMax = 0
let threshold = 0
for (let t = 0; t < 256; t++) {
wB += histData[t]
if (wB === 0) continue
wF = total - wB
if (wF === 0) break
sumB += t * histData[t]
let mB = sumB / wB
let mF = (sum - sumB) / wF
let varBetween = wB * wF * (mB - mF) ** 2
if (varBetween > varMax) {
varMax = varBetween
threshold = t
}
}
return threshold
}OTSUAlgorithm() 函数接收一个 ImageData 对象,经过上一步的 toGray() 方法获取到灰度值列表以后,根据“大津法”算出最佳阈值然后返回。接下来使用这个阈值对原图进行处理,即可获取二值图。
export function binaryzation (imgData: ImageData, threshold: number) {
const canvas = document.createElement('canvas')
const ctx = canvas.getContext('2d')
const imgWidth = Math.sqrt(imgData.data.length / 4)
const newImageData = ctx?.createImageData(imgWidth, imgWidth) as ImageData
for (let i = 0; i < imgData.data.length; i += 4) {
let R = imgData.data[i]
let G = imgData.data[i + 1]
let B = imgData.data[i + 2]
let Alpha = imgData.data[i + 3]
let sum = (R + G + B) / 3
newImageData.data[i] = sum > threshold ? 255 : 0
newImageData.data[i + 1] = sum > threshold ? 255 : 0
newImageData.data[i + 2] = sum > threshold ? 255 : 0
newImageData.data[i + 3] = Alpha
}
return newImageData
}若图片大小为 N×N,根据二值图“非黑即白”的特性,我们便可以得到一个 N×N 的 0-1 矩阵,也就是指纹:
特征比对算法
经过不同的方式取得不同类型的图片指纹(特征)以后,应该怎么去比对呢?这里将介绍三种比对算法,然后分析这几种算法都适用于哪些情况。
汉明距离
摘一段维基百科关于“汉明距离”的描述:
在信息论中,两个等长字符串之间的汉明距离(英语:Hamming distance)是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
例如:
- 1011101与1001001之间的汉明距离是2。
- 2143896与2233796之间的汉明距离是3。
- "toned"与"roses"之间的汉明距离是3。
明白了含义以后,我们可以写出计算汉明距离的方法:
export function hammingDistance (str1: string, str2: string) {
let distance = 0
const str1Arr = str1.split('')
const str2Arr = str2.split('')
str1Arr.forEach((letter, index) => {
if (letter !== str2Arr[index]) {
distance++
}
})
return distance
}使用这个 hammingDistance() 方法,来验证下维基百科上的例子:
验证结果符合预期。
知道了汉明距离,也就可以知道两个等长字符串之间的相似度了(汉明距离越小,相似度越大):
相似度 = (字符串长度 - 汉明距离) / 字符串长度余弦相似度
从维基百科中我们可以了解到关于余弦相似度的定义:
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这结果是与向量的长度无关的,仅仅与向量的指向方向相关。余弦相似度通常用于正空间,因此给出的值为0到1之间。注意这上下界对任何维度的向量空间中都适用,而且余弦相似性最常用于高维正空间。
余弦相似度可以计算出两个向量之间的夹角,从而很直观地表示两个向量在方向上是否相似,这对于计算两个 N×N 的 0-1 矩阵的相似度来说非常有用。根据余弦相似度的公式,我们可以把它的 js 实现写出来:
export function cosineSimilarity (sampleFingerprint: number[], targetFingerprint: number[]) {
// cosθ = ∑n, i=1(Ai × Bi) / (√∑n, i=1(Ai)^2) × (√∑n, i=1(Bi)^2) = A · B / |A| × |B|
const length = sampleFingerprint.length
let innerProduct = 0
for (let i = 0; i < length; i++) {
innerProduct += sampleFingerprint[i] * targetFingerprint[i]
}
let vecA = 0
let vecB = 0
for (let i = 0; i < length; i++) {
vecA += sampleFingerprint[i] ** 2
vecB += targetFingerprint[i] ** 2
}
const outerProduct = Math.sqrt(vecA) * Math.sqrt(vecB)
return innerProduct / outerProduct
}
两种比对算法的适用场景
明白了“汉明距离”和“余弦相似度”这两种特征比对算法以后,我们就要去看看它们分别适用于哪些特征提取算法的场景。
首先来看“颜色分布法”。在“颜色分布法”里面,我们把一张图的颜色进行区间划分,通过统计不同颜色区间的数量来获取特征,那么这里的特征值就和“数量”有关,也就是非 0-1 矩阵。
显然,要比较两个“颜色分布法”特征的相似度,“汉明距离”是不适用的,只能通过“余弦相似度”来进行计算。
接下来看“平均哈希算法”和“内容特征法”。从结果来说,这两种特征提取算法都能获得一个 N×N 的 0-1 矩阵,且矩阵内元素的值和“数量”无关,只有 0-1 之分。所以它们同时适用于通过“汉明距离”和“余弦相似度”来计算相似度。
计算精度
明白了如何提取图片的特征以及如何进行比对以后,最重要的就是要了解它们对于相似度的计算精度。
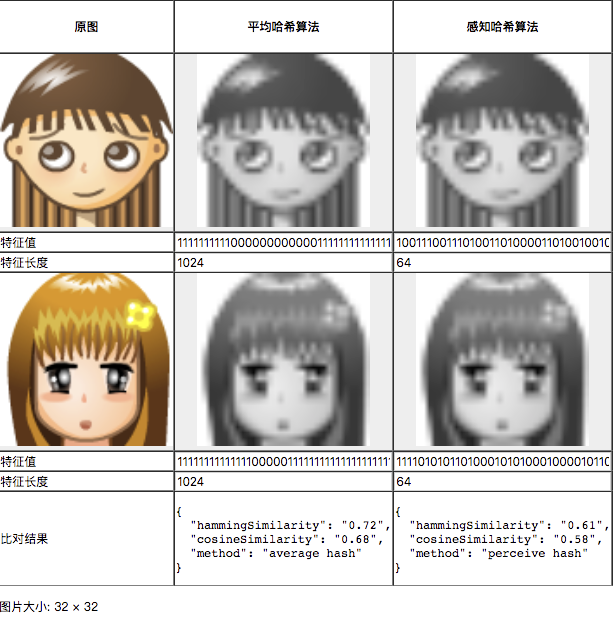
本文所讲的相似度仅仅是通过客观的算法来实现,而判断两张图片“像不像”却是一个很主观的问题。于是我写了一个简单的服务,可以自行把两张图按照不同的算法和精度去计算相似度:
https://img-compare.netlify.com/
经过对不同素材的多方比对,我得出了下列几个非常主观的结论。
- 对于两张颜色较为丰富,细节较多的图片来说,“颜色分布法”的计算结果是最符合直觉的。
- 对于两张内容相近但颜色差异较大的图片来说,“内容特征法”和“平均/感知哈希算法”都能得到符合直觉的结果。
- 针对“颜色分布法“,区间的划分数量对计算结果影响较大,选择合适的区间很重要。
总结一下,三种特征提取算法和两种特征比对算法各有优劣,在实际应用中应该针对不同的情况灵活选用。
总结
本文是在拜读阮一峰的两篇《相似图片搜索的原理》之后,经过自己的实践总结以后而成。由于对色彩、数学等领域的了解只停留在浅显的层面,文章难免有谬误之处,如果有发现表述得不正确的地方,欢迎留言指出,我会及时予以更正。


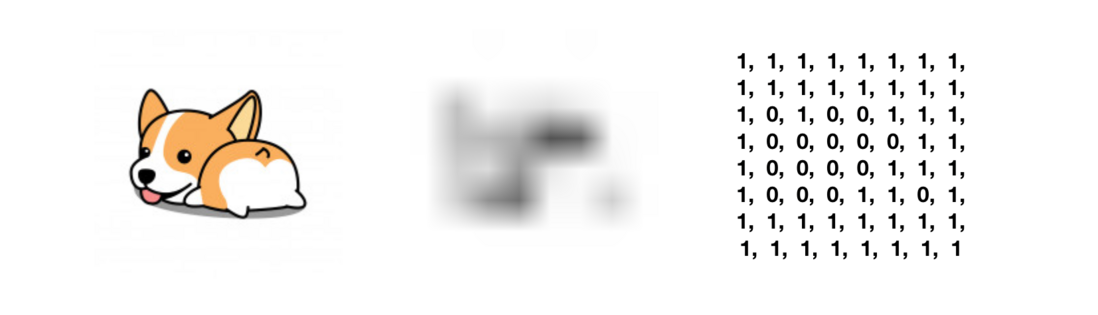








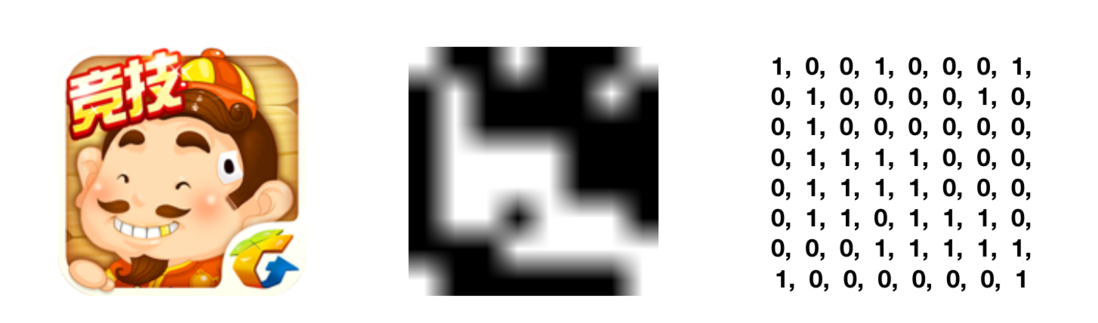





**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。