[数据结构基础] 掌握树的四种遍历方式，以及BFS, DFS

头像
皮小蛋
    阅读 9 分钟
    12

    背景

    上一篇文章， 我们熟悉了树， 二叉树， 二叉搜索树的基本概念， 以及做了对应的实战题目：

    树， 二叉树， 二叉搜索树 && 实战练习

    今天我们继续树这个话题。

    本文的主要内容包括：

    • 理论：树的前中后遍历
    • 理论：广度优先搜索
    • 理论：深度优先搜索
    • 理论：树的层次遍历
    • 实战：Leetcode题目演练

    树是一种比较常见的数据结构， 面试中也比较常见。

    熟悉树的前中后序遍历，只是让大家明白树的遍历可以有不同的顺序， 实际的应用也比较少， 意义并不大，但是作为基础， 我们还是要学一下这部分。

    基本上，真正的遍历还是要看深度优先和广度优先遍历。

    废话不多说， 我们进入正文。

    正文

    树的前中后序遍历

    这三种遍历的顺序是十分好记的：

    • 前序： 根左右
    • 中序： 左根右
    • 后序： 左右根

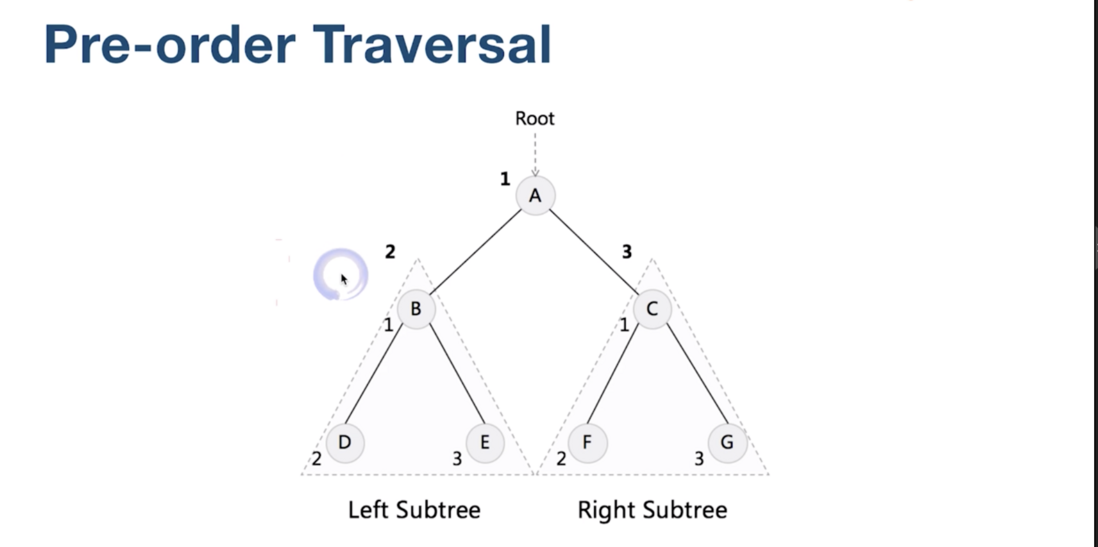
    前序遍历

    image.png

    如图所示， 这样的一棵二叉树的前序遍历,

    先访问根结点， 然后是左子树， 再然后是右子树。

    遍历的结果就是：

    A， B， D， E， C， F， G

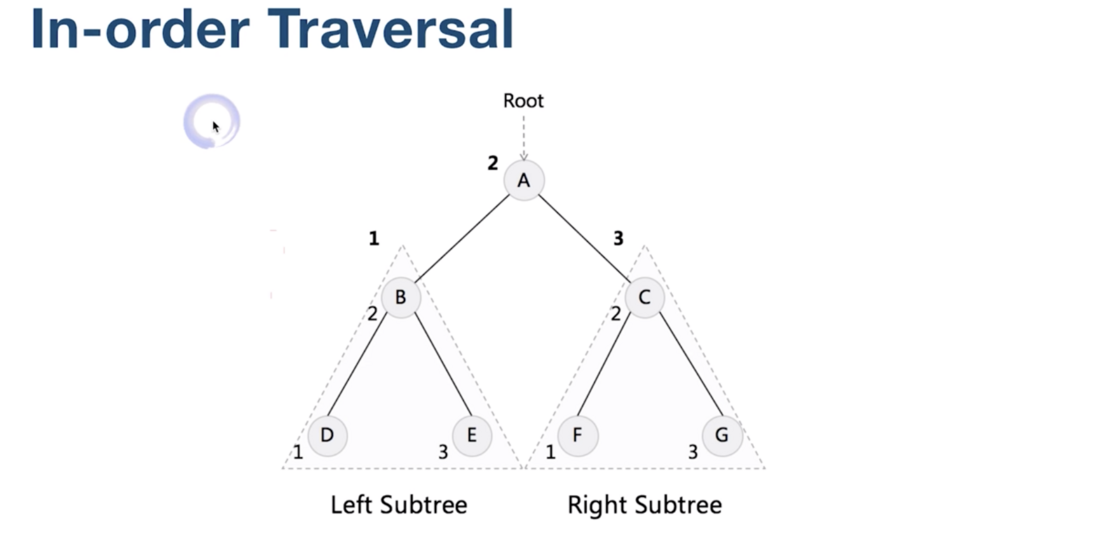
    中序遍历

    image.png

    先访问的是左子树， 然后是根， 再然后是右子树。

    遍历的结果就是：

    D, B, E, A, F, C, G

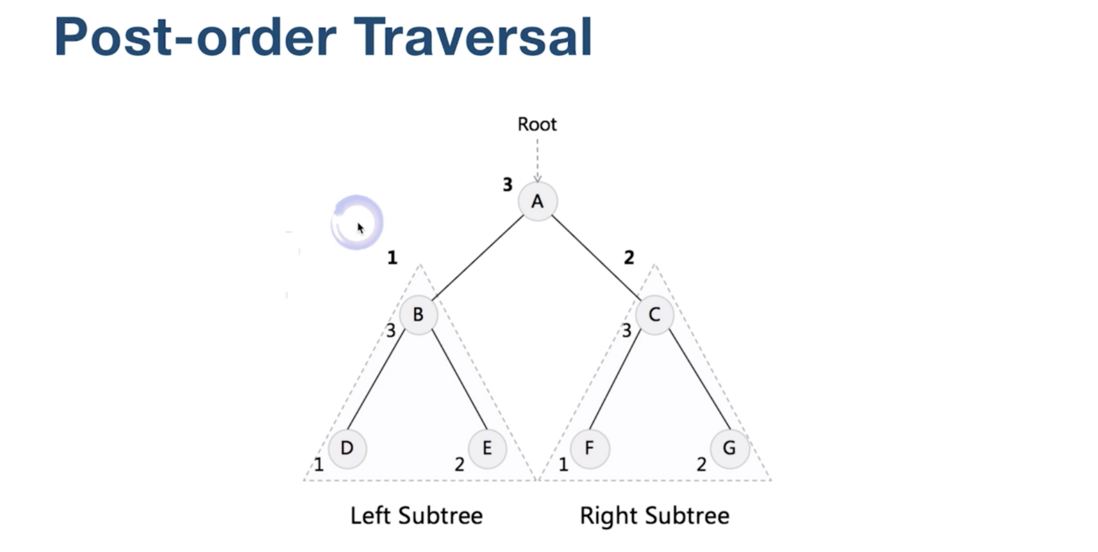
    后序遍历

    image.png

    先访问的是左子树， 然后是右子树， 再然后是根。

    遍历的结果就是：

    D, E, B, F, G, C, A

    前中后序遍历的代码实现 - medium

    如果你对这三种遍历非常熟悉， 在面对验证二叉搜索树这类问题的时候， 就知道可以用中序遍历的特性来验证。

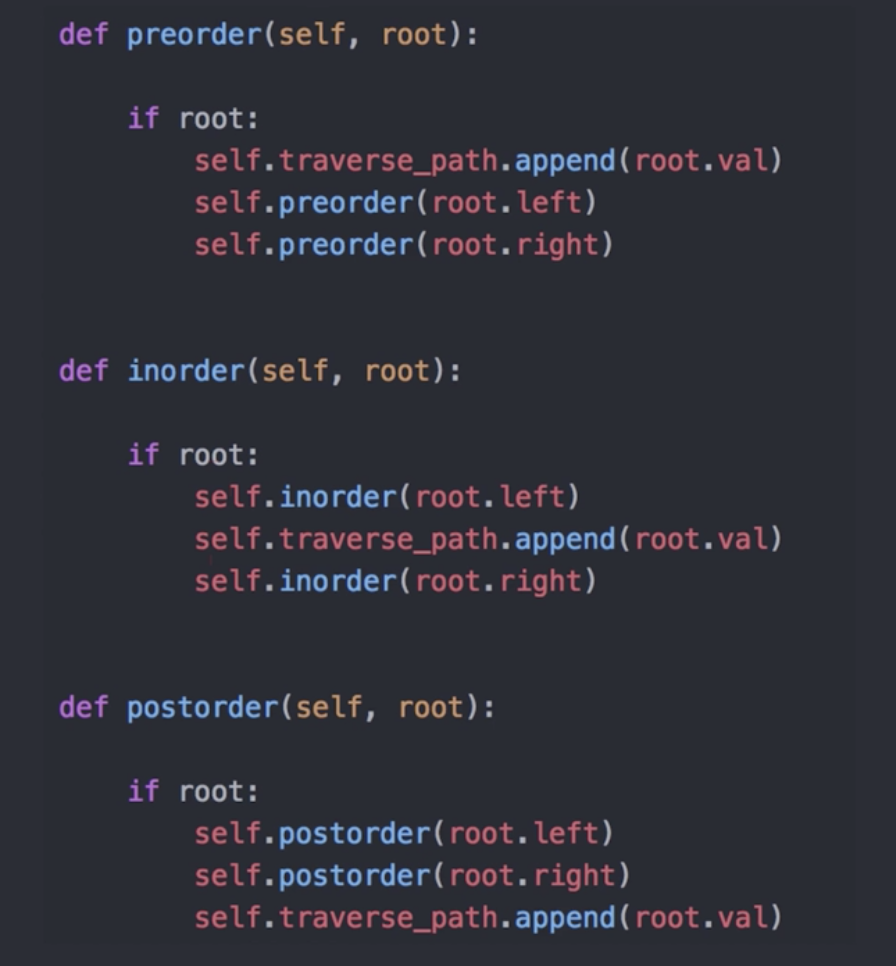
    下面我们就大概看一下这三种遍历的逻辑实现。

    这里借用来自社区大佬的Python实现， 非常的优雅：
    image.png

    leetcode 上也有这三种遍历的题目， 因为不是本文重点，所以就用递归简单实现一下：

    144 前序遍历的简单实现 - medium
    给定一个二叉树，返回它的 _前序 _遍历。
    输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [1,2,3]

    代码实现：

    var preorderTraversal = function (root) {
    var stack = []

    function helper(root) {
        if (!root) return
        stack.push(root.val)
        root.left && helper(root.left)
        root.right && helper(root.right)
    }

    helper(root)

    return stack
}

    image.png

    94: 中序遍历的简单实现
    给定一个二叉树，返回它的中序 遍历。
    示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]

    代码实现：

    var inorderTraversal = function (root) {
    var stack = []

    function helper(root) {
        if (!root) return

        root.left && helper(root.left)
        stack.push(root.val)
        root.right && helper(root.right)
    }

    helper(root)

    return stack
};

    image.png

    145: 后序遍历的简单实现 - hard
    给定一个二叉树，返回它的 后序 遍历。
    示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [3,2,1]

    代码实现：

    var postorderTraversal = function (root) {
    var stack = []

    function helper(root) {
        if (!root) return

        root.left && helper(root.left)
        root.right && helper(root.right)
        stack.push(root.val)
    }

    helper(root)

    return stack
}

    image.png

    第一部分小结

    上面这部分， 我们熟悉了二叉树的三种遍历方式， 并熟悉了三道实战题目， 下面我们就正式接触今天的主角: BFS & DFS。

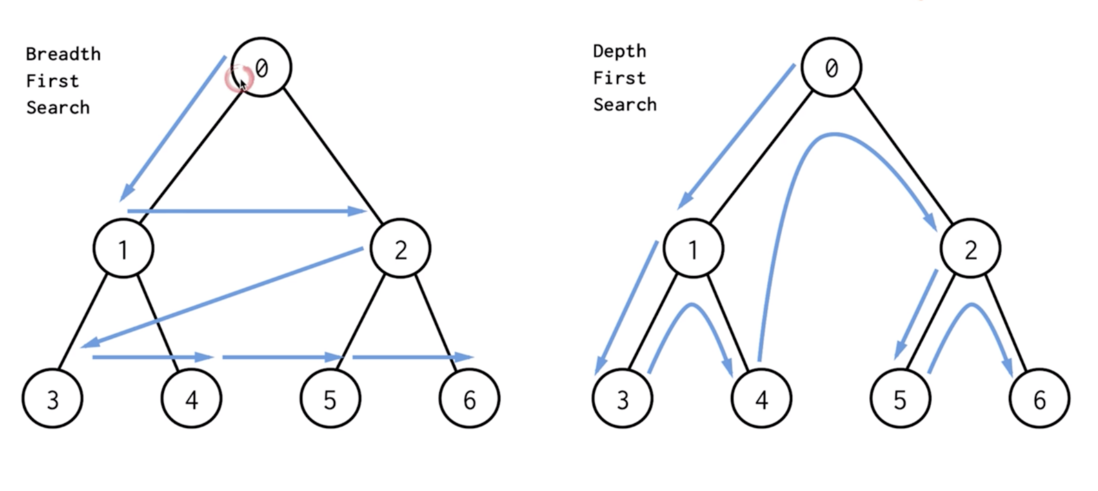
    广度优先搜索

    广度优先搜索(Breadth-First-Search), 简称BFS，是一种比较常见的二叉树搜索方式。

    先说一下， 为什么会出现这种搜索方式吧。

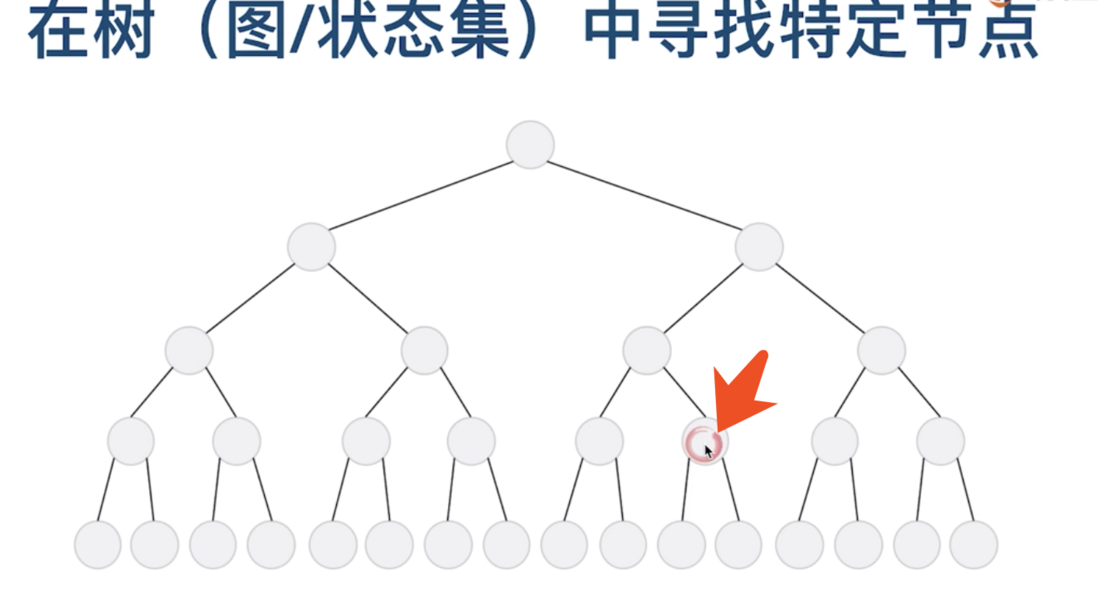
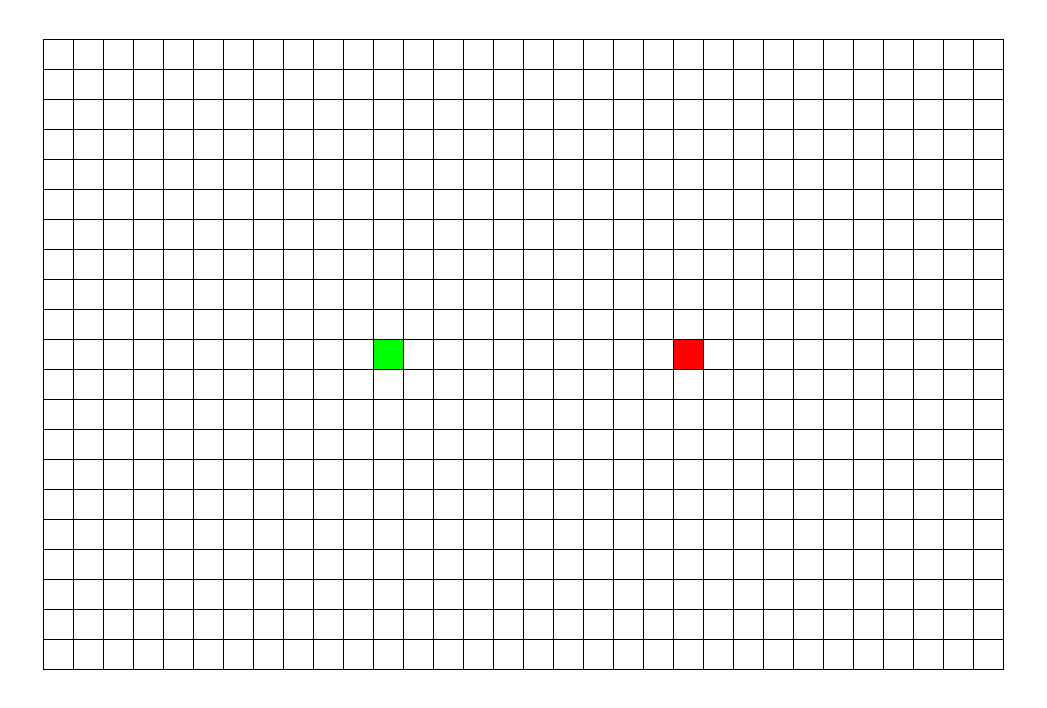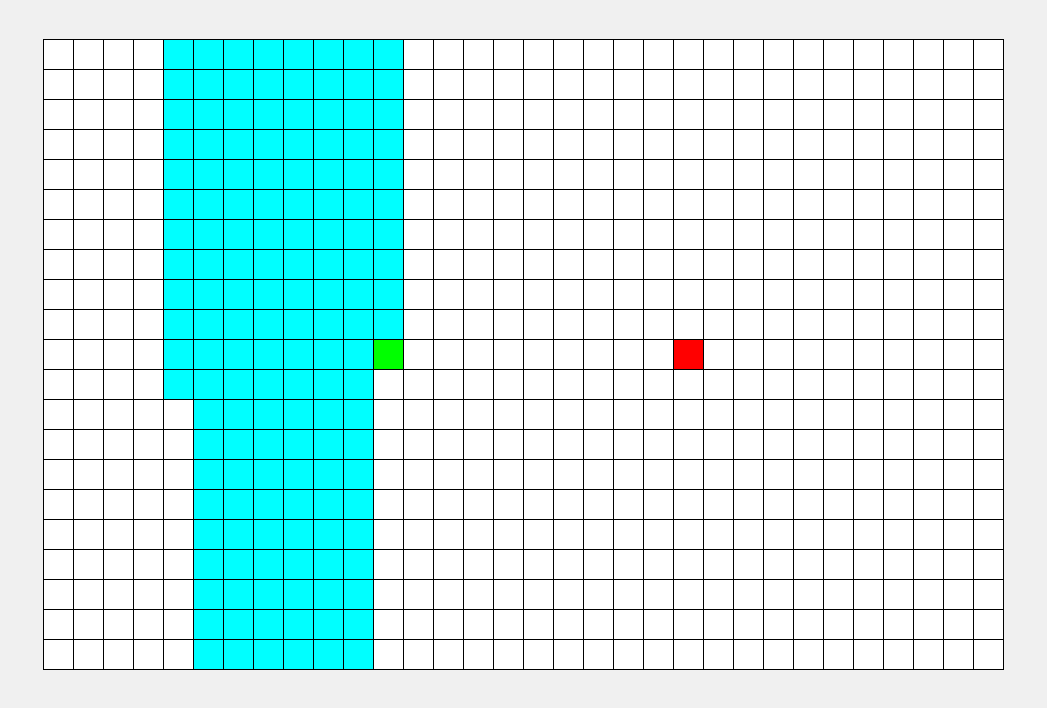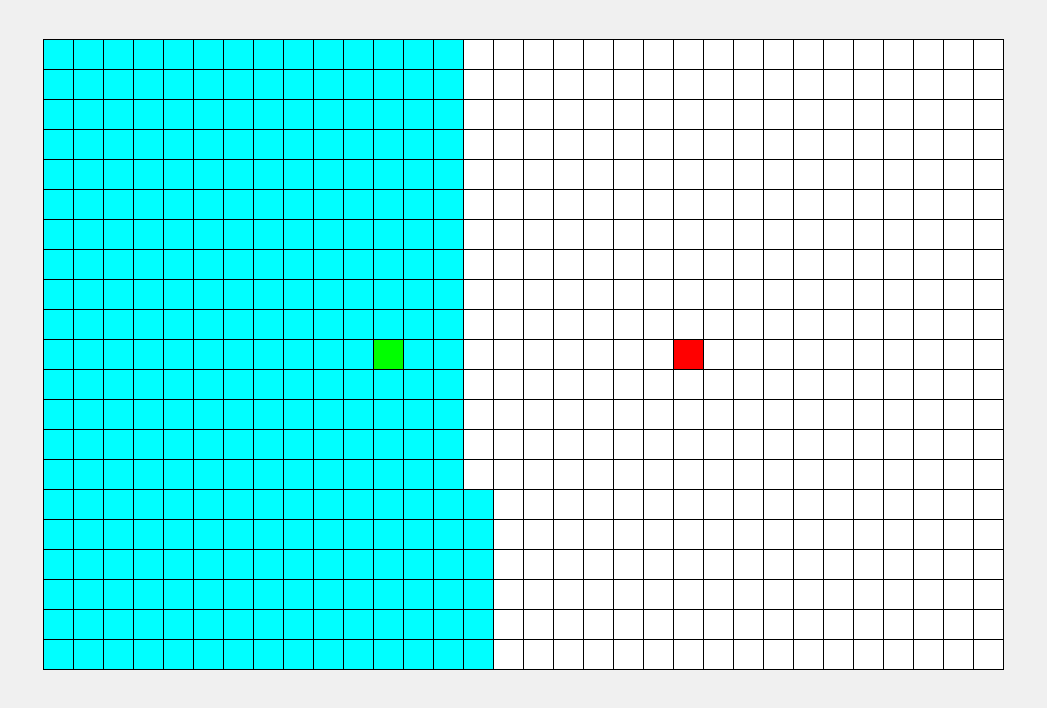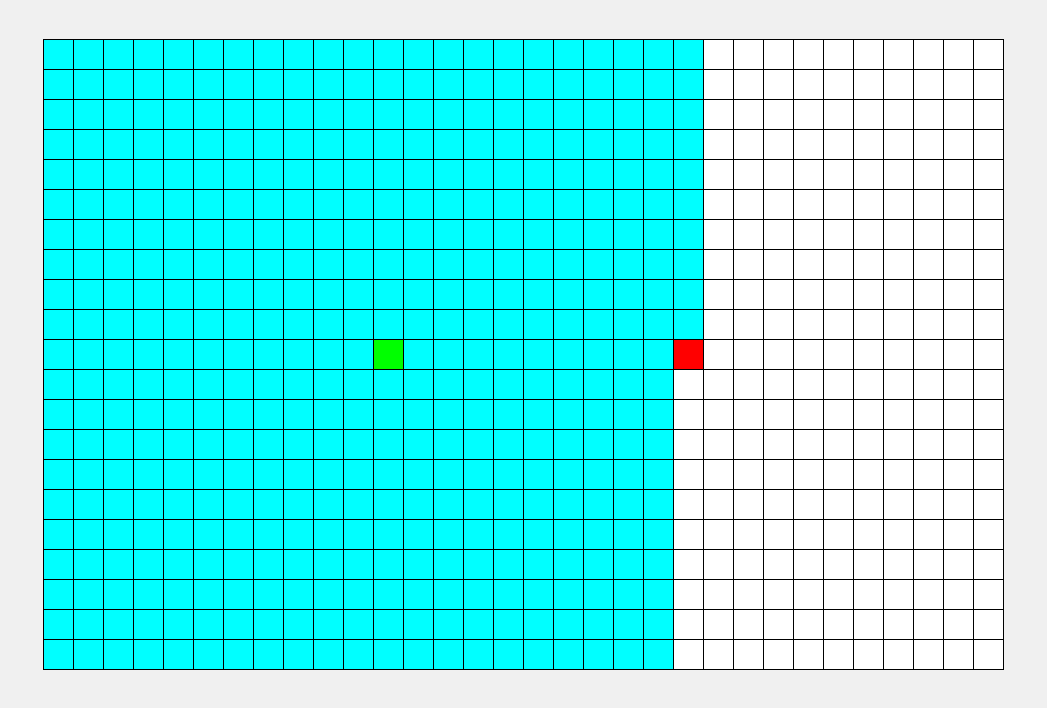
    比如， 我们在生活中， 需要在一个大的集合中， 找到某个特定的元素，这个集合可能是一个状态集，也可能是一些树，或者图。

    image.png

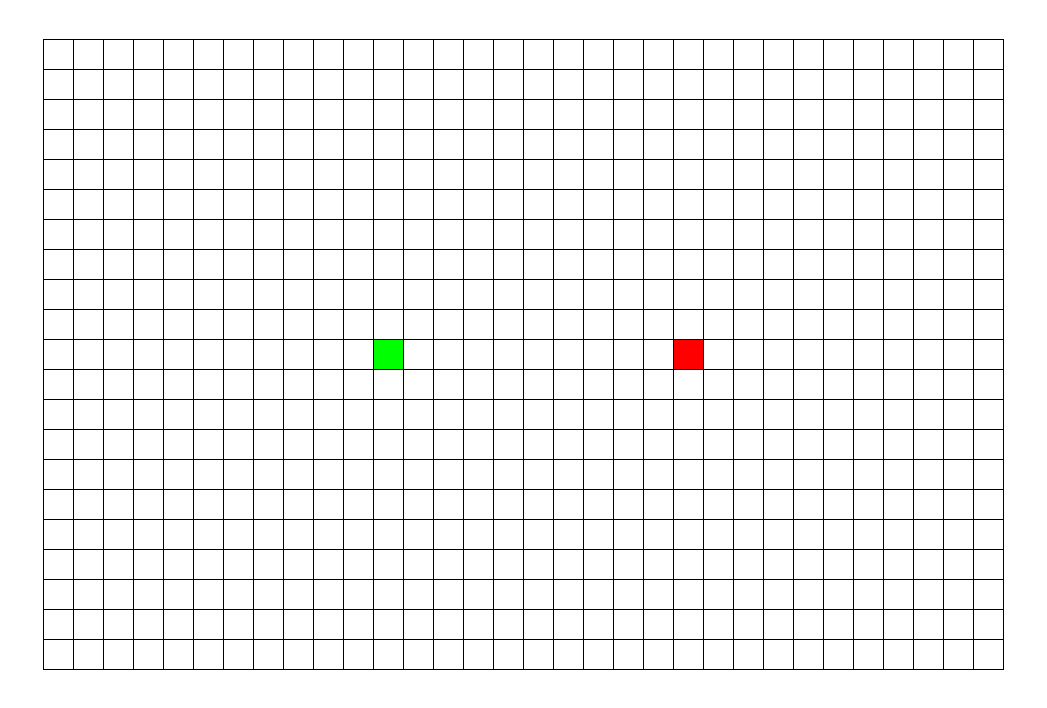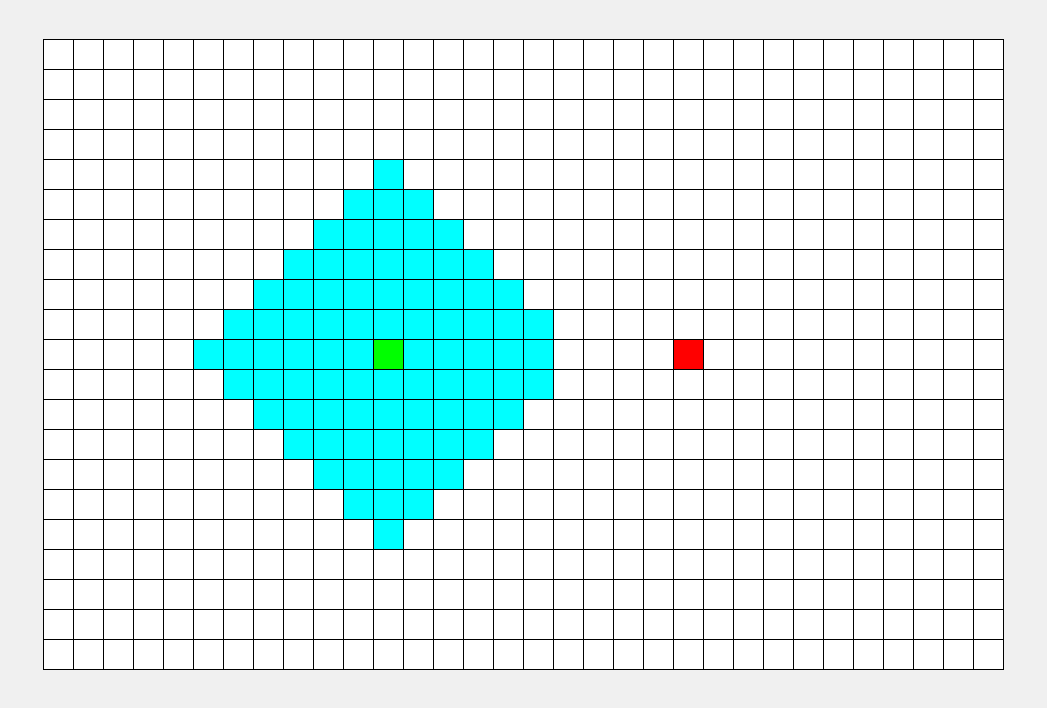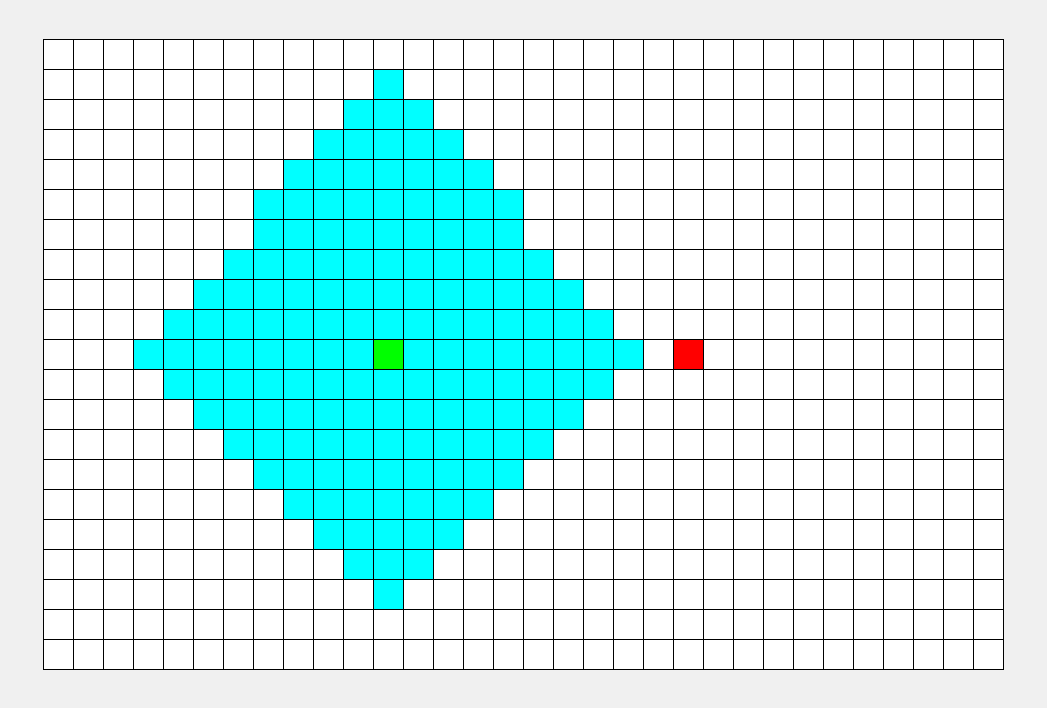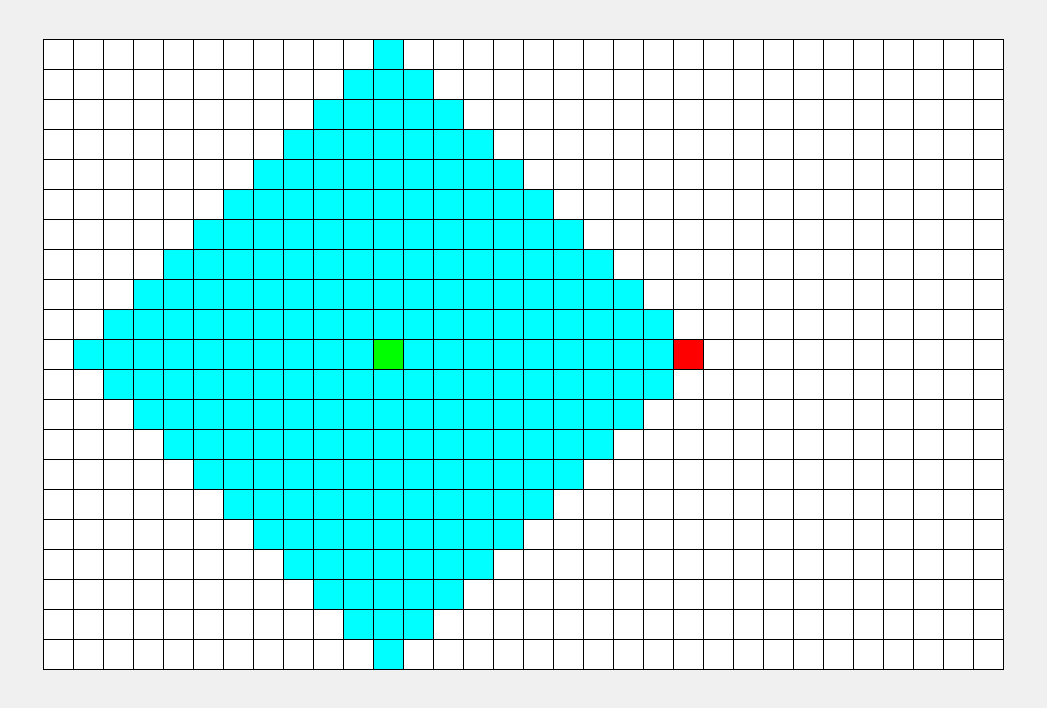
    比如， 我们要找到箭头所指的这个点， 该怎么找呢？

    我们最直观的反应就是，层层递进， 一层一层往下搜索。

    这种最符合我们思维方式的搜索方式就是广度优先搜索。

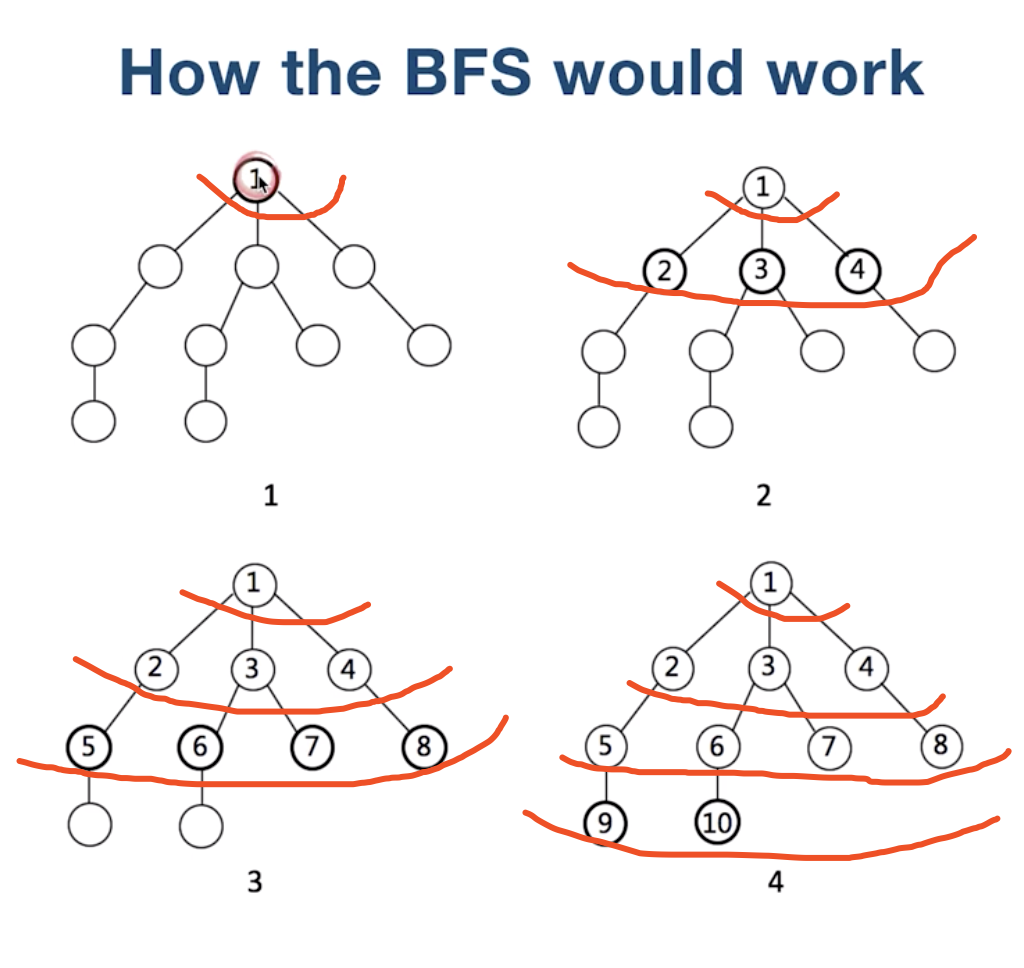
    下面我们看一下这种方式具体是怎么搜索的。

    image.png

    首先， 访问的是根结点1。

    接下来， 依次访问1的孩子，就是2, 3, 4结点， 依次类推。

    就像水波一样， 一层一层往前推， 比较符合人类的思维习惯。

    算法基础：BFS和DFS的直观解释

    BFS的实现思路也比较直观：

    从1开始， 依次把儿子结点放到队列中去， 遍历的结点依次放入队列之中，队列是先入先出的，这样就达到了层次遍历的效果。

    BFS的实现

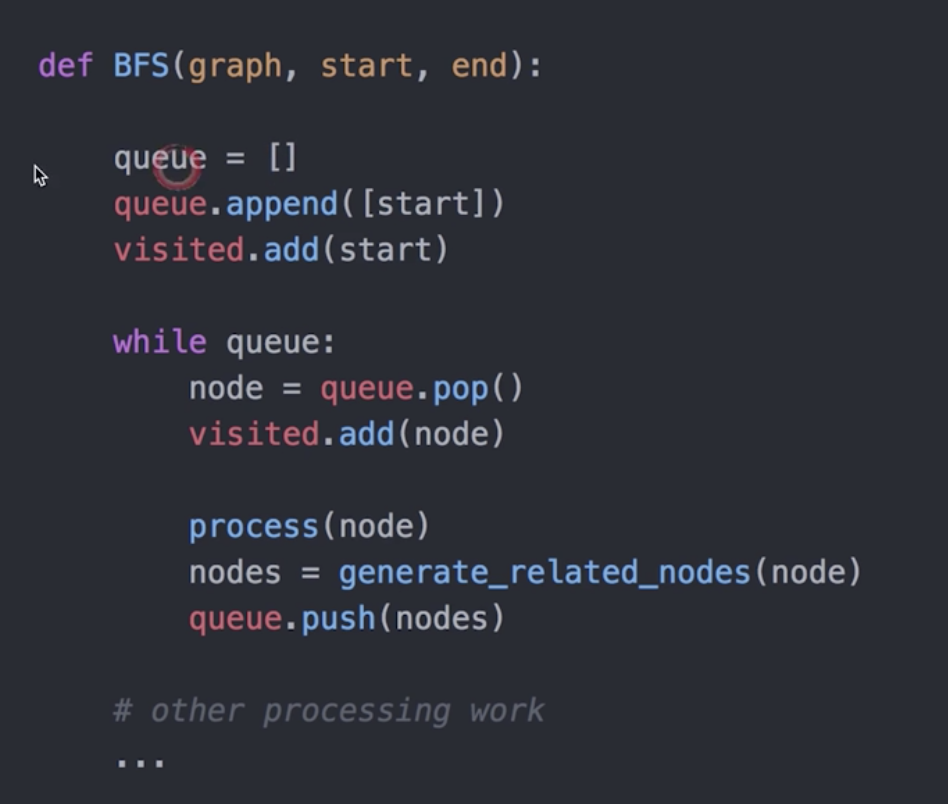
    BFS伪代码实现：

    即刻时间课程截图.png

    为了避免重复搜索， 引入了判重的set， 来记录已经搜索过的结点。

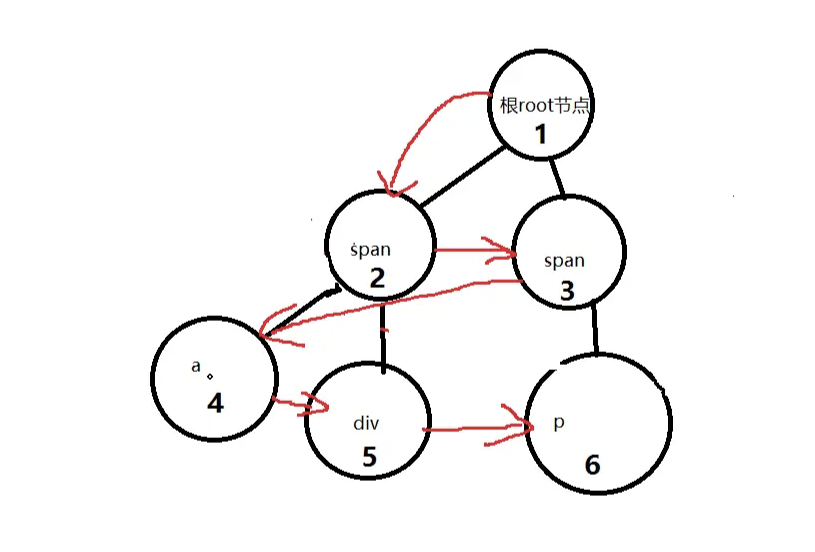
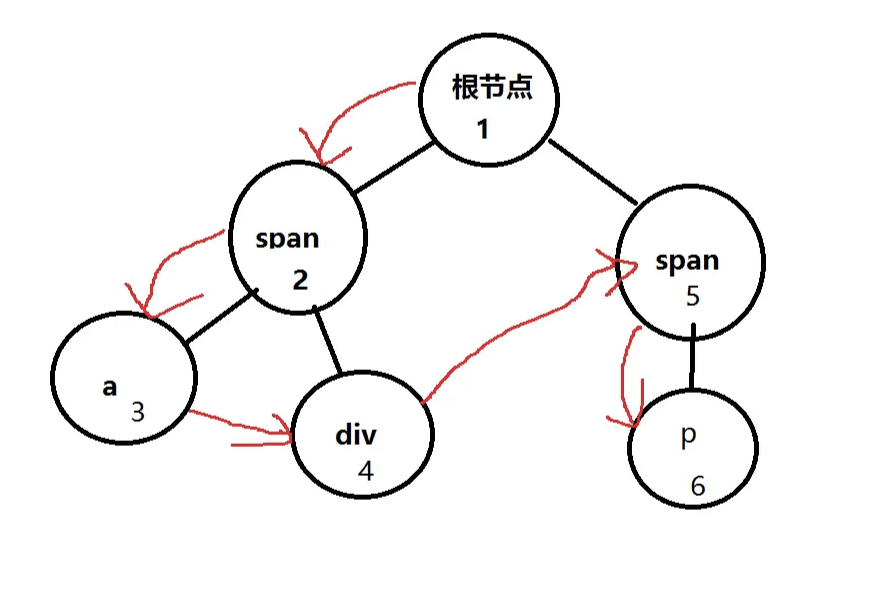
    下面我们看一个具体的例子：

    有如下html结构，要求分层打印出每个节点：

    <div id='root'>
    <span>
        <a></a>
        <div></div>
    </span>
    <span>
        <p></p>
    </span>
</div>

    image.png

    function BFS(node) {  
    var nodes = [];  
    if (node != null) {  
        var queue = [];  
        queue.unshift(node);  
        while (queue.length !== 0) {  
            var item = queue.shift(); // 取出第一个元素
            nodes.push(item);  
            var children = item.children;  
            for (var i = 0; i < children.length; i++) {
              queue.push(children[i]);  
            }     
        }  
    }  
    return nodes;  
}
var root = document.getElementById('root');
console.log(BFS(root));

    image.png

    下面我们继续看深度优先搜索。

    深度优先搜索

    深度优先搜索 - Depth First Search, 简称DFS。

    BFS，使用的是队列， 先入先出。
    DFS，使用的是栈， 先入后出。

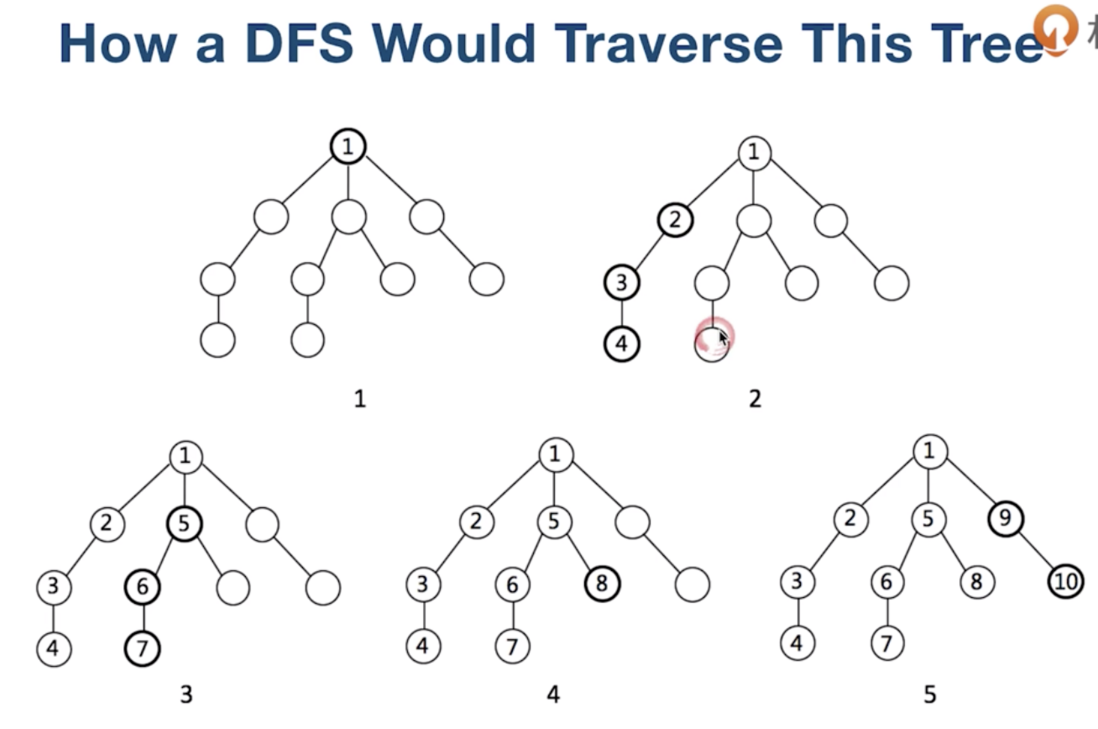
    DFS， 这种方式， 比较耿直， 一根筋，一插到底， 到头位置。

    即刻时间课程截图.png

    DFS的直观解释


    BDS， DFS的简单的对比：

    image.png

    DFS的实现

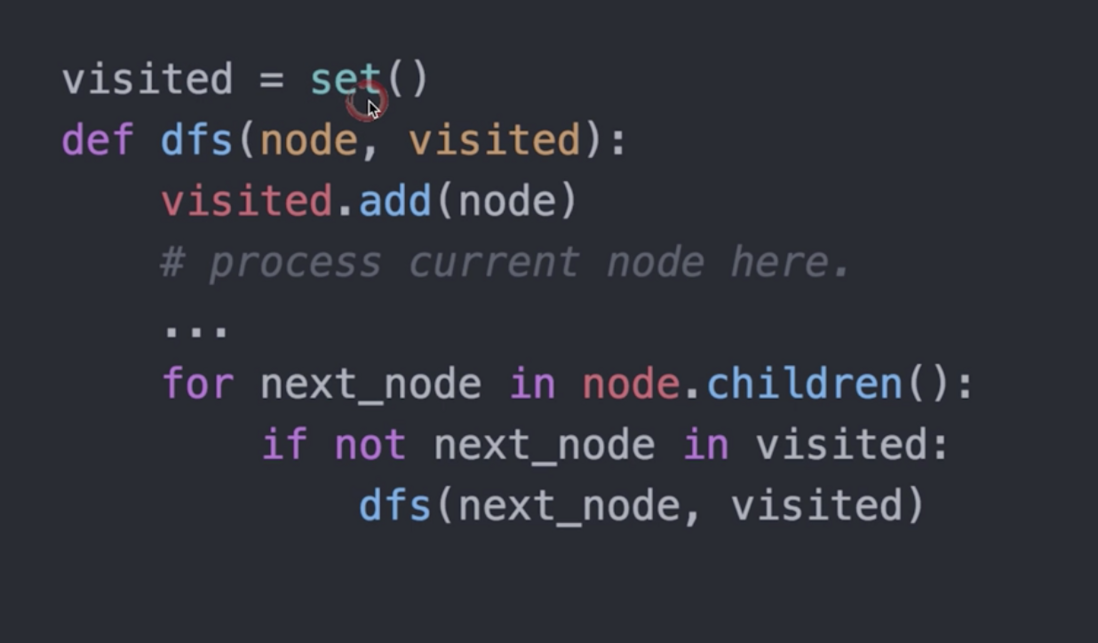
    DFS递归伪代码(推荐)：

    image.png

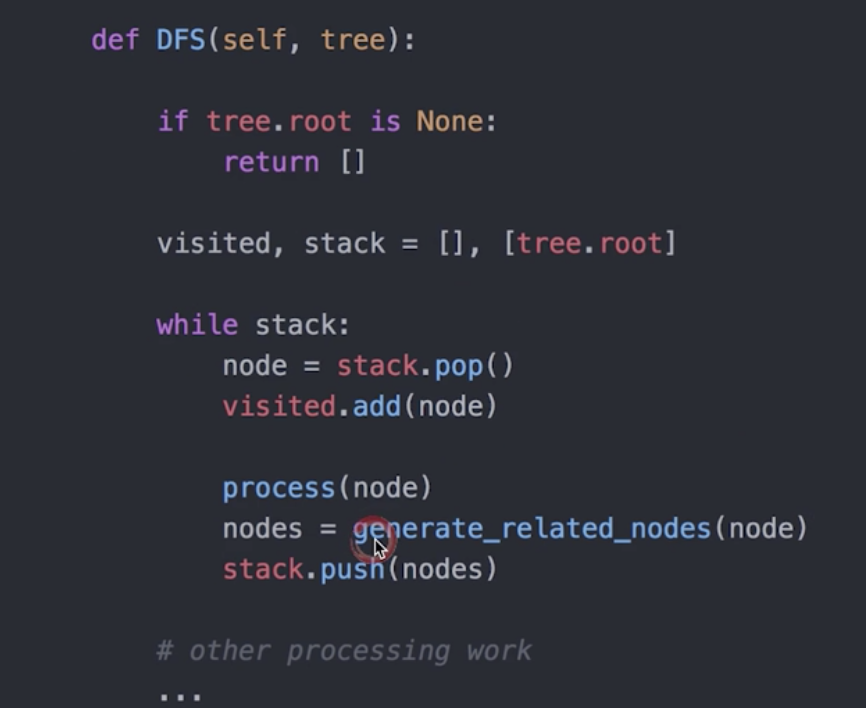
    DFS非递归伪代码：

    image.png

    了解完思路， 我们再回到开头遍历DOM结点那道题。

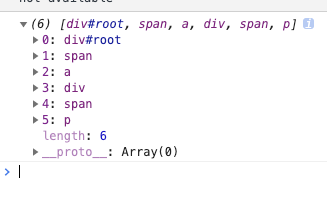
    现在要求用DFS的方式来打印结点。

    <div id='root'>
    <span>
        <a></a>
        <div></div>
    </span>
    <span>
        <p></p>
    </span>
</div>

    image.png

    我们用递归和非递归两种方式实现。

    1. 递归
      function DFS(node, nodeList) {
      if (node) {
          nodeList.push(node);
          var children = node.children;
          for (var i = 0; i < children.length; i++) {
              DFS(children[i], nodeList);
          }
      }
      return nodeList;
  }
  var root = document.getElementById('root')
  console.log(DFS(root, []))

    image.png

    2. 非递归
    function DFS(node) {
    var nodeList = [];
    if (node) {
        var stack = [];
        stack.push(node);
        while (stack.length !== 0) {
            var childrenItem = stack.pop();
            nodeList.push(childrenItem);
            var childrenList = childrenItem.children;
            for (var i = childrenList.length - 1; i >= 0; i--) {
                stack.push(childrenList[i]);
            }
        }
    }
    return nodeList;
}
var root = document.getElementById('root')
console.log(DFS(root))

    image.png

    推荐第一种递归的写法， 更容易理解， 也不需要额外的维护数据结构， 非递归的方式理解即可。

    简单的小结

    对于这BFS， DFS两个搜索方法，其实我们是可以轻松的看出来，他们有许多差异与许多相同点的。

    1.数据结构上的运用

    BFS, 选取状态用队列的形式，先进先出。
    DFS, 用递归的形式，用到了栈结构，先进后出。

    2.复杂度

    DFS的复杂度与BFS的复杂度大体一致，不同之处在于遍历的方式与对于问题的解决出发点不同，DFS适合目标明确，而BFS适合大范围的寻找。

    3.思想

    思想上来说这两种方法都是穷竭列举所有的情况。

    树的层次遍历

    层次遍历， 也叫 Level Order Search。

    故名思意， 就是按层来遍历, 和BFS 十分类似。

    image.png

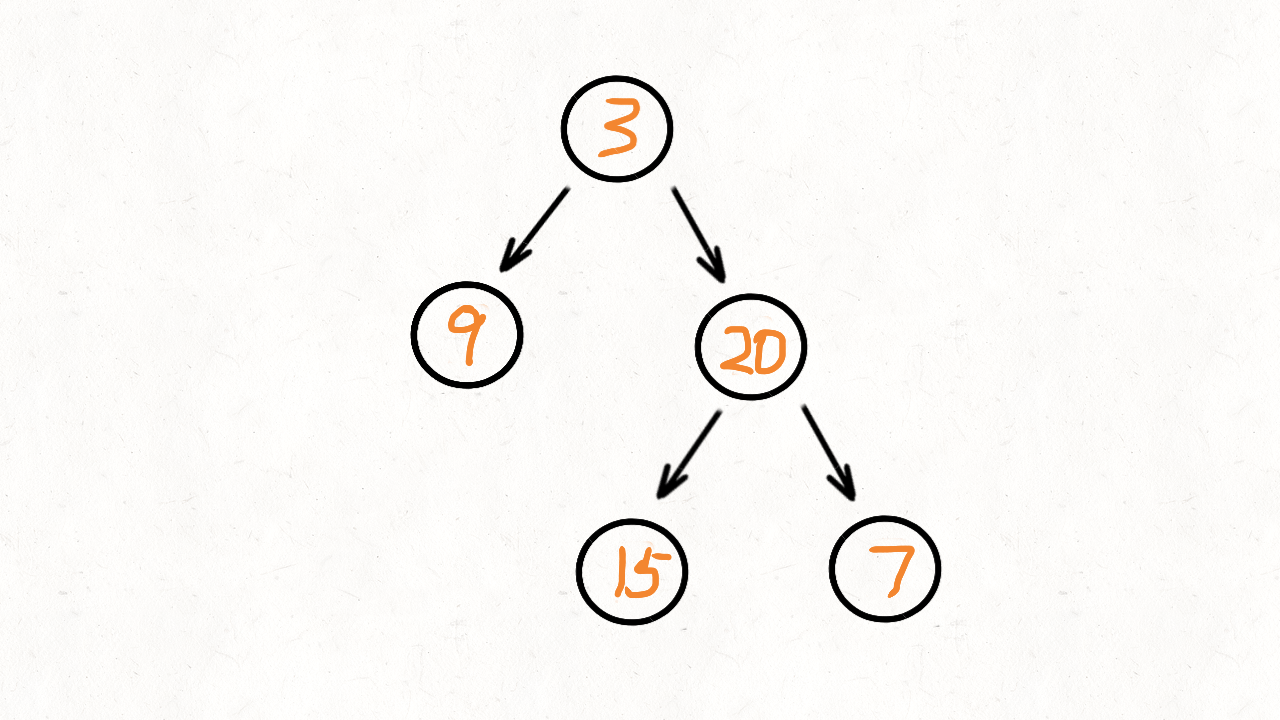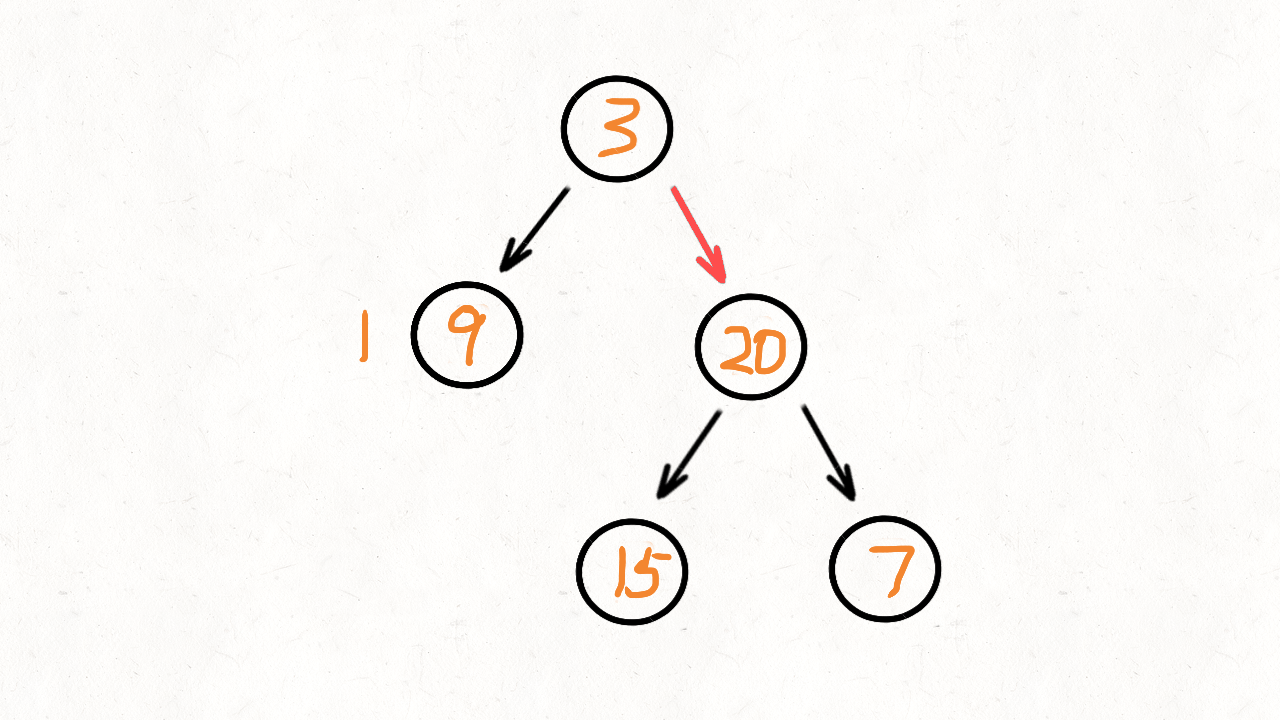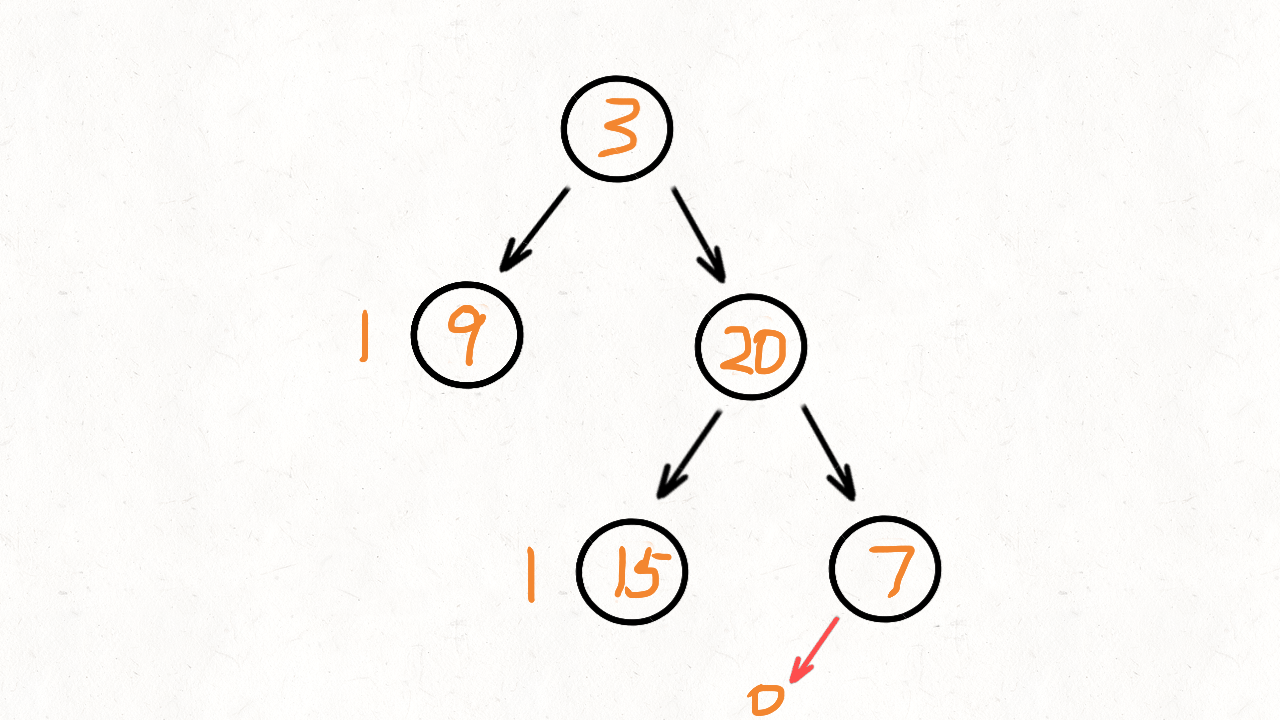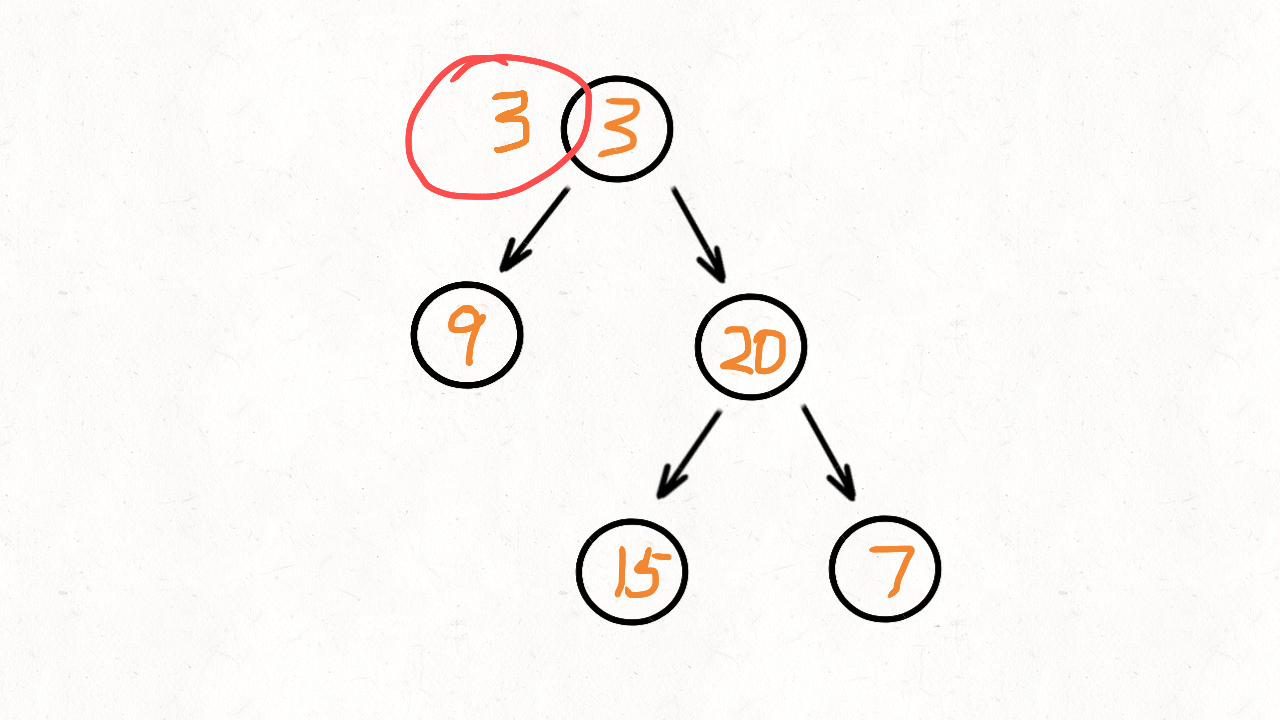
    比如这样一棵二叉树：

        3
   / \
  9  20
    /  \
   15   7

    层次遍历的结果就是： 3, 9, 20, 15, 7

    leetcode 上就有这么一道题目， 二叉树的层次遍历， 我们就一起来做一下， 进入实战环节。

    实战题目

    Leetcode-102: 二叉树的层次遍历

    给定一个二叉树，返回其按层次遍历的节点值。 （即逐层地，从左到右访问所有节点）。
    例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

    实现的方式有很多， 比如BFS。

    一种BFS的代码实现：

    /**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
    if (!root) return []
    let result = [], queue = [root]

    while (queue.length) {
        let currentLevel = []
        let levelSize = queue.length
        while (levelSize !== 0) {
            let node = queue.shift()
            currentLevel.push(node.val)
            if (node.left) queue.push(node.left)
            if (node.right) queue.push(node.right)
            levelSize--
        }
        result.push(currentLevel)
    }

    return result
};

    image.png

    这道题， 也可以用 DFS 来实现，这里给你一种Java 的实现， 你可以理解一下思路， 然后自己实现一遍。
    image.png

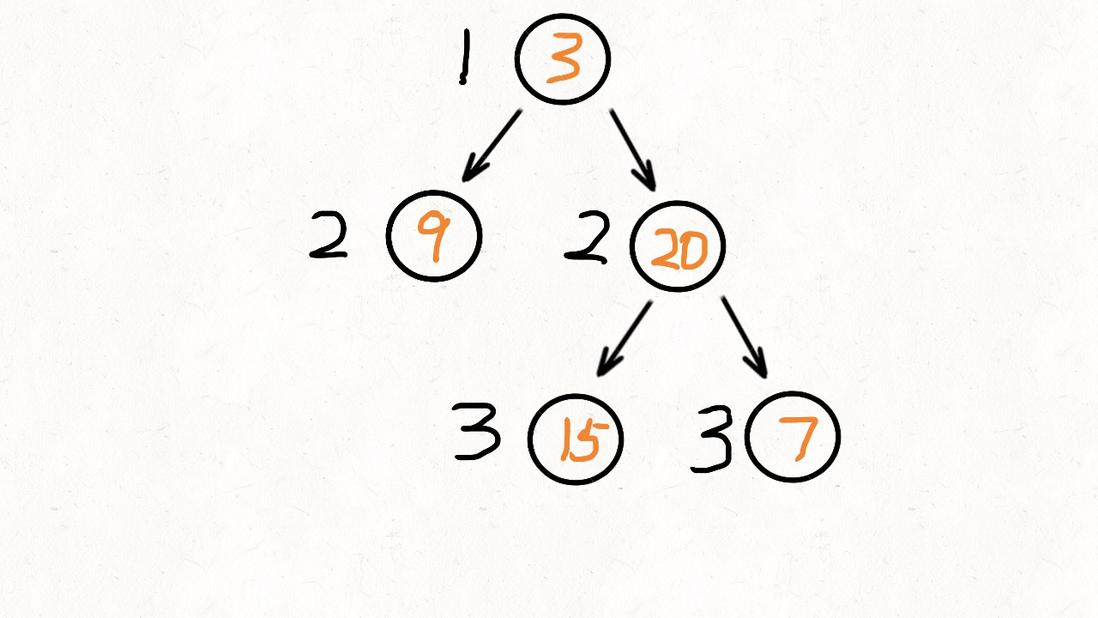
    Leetcode 104, 二叉树的最大深度

    给定一个二叉树，找出其最大深度。

    二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

    说明: 叶子节点是指没有子节点的节点。

    示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。
    解法1. 递归

    递归-动态图.gif

    var maxDepth = function(root) {
    if(!root) return 0
    
    var left = maxDepth(root.left) + 1
    var right = maxDepth(root.right) + 1
    // +1 是算上根结点的高度
    
    return left > right ? left : right
}

    解法2: 用队列实现-BFS

    遍历每一层的节点高度，然后求得最深的一个节点的高度，就是整个树的高度了。

    queue_1.jpg

    var maxDepth = function (root) {
    if (!root) return 0

    let queue = []
    let depth = 0

    queue.push(root)

    while (queue.length) {
        depth++
        let size = queue.length

        while (size > 0) {
            let p = queue.shift()
            if (p.left) queue.push(p.left)
            if (p.right) queue.push(p.right)
            size--
        }
    }

    return depth
};

    image.png

    解法3: 用队列实现-DFS

    基本思路：

    首先访问根结点然后遍历左子树，最后遍历右子树。

    从包含根结点且相应深度为 1 的栈开始。

    然后将当前结点弹出栈并推入子结点, 每一步都会更新深度。

    时间复杂度：O(N)
    空间复杂度：O(N)

    代码实现：

    var maxDepth = function (root) {
    if (!root) return 0

    let stack = []
    let depthStack = []
    let depth = 1

    stack.push(root)
    depthStack.push(depth)

    while (stack.length > 0) {
        let node = stack.pop()
        let temp = depthStack.pop()

        if (depth < temp) depth = temp

        if (node.right) {
            stack.push(node.right)
            depthStack.push(temp + 1)
        }

        if (node.left) {
            stack.push(node.left)
            depthStack.push(temp + 1)
        }
    }

    return depth
}

    image.png

    还有 第101题，二叉树的最大深度， 思路都是类似的， 这里就不解了， 留给你练习。

    结语

    作文本年度的最后一篇文章，写了一天多， 终于写完了....

    树的深搜和广搜， 是非常重要的两种搜索方式， 也是面试中的重点。

    希望本文能对你有所帮助。

    最后

    觉得内容有帮助可以关注下我的公众号 「 前端e进阶 」，一起学习。

    clipboard.png

    数据结构前端vue.jsreactnode.js
    皮小蛋
    8k 声望12.8k 粉丝

    积跬步，至千里。

    « 上一篇
    树， 二叉树， 二叉搜索树 && 实战练习
    下一篇 »
    2020, 新年Flag 走起～

    引用和评论

    推荐阅读
    头像
    我在 Shopee 毕业啦

    皮小蛋赞 1阅读 2.1k评论 6

    头像
    网页设计的垂直居中

    寒青赞 41阅读 5.2k评论 3

    头像
    CSS团队协作规范

    寒青赞 38阅读 7.4k

    头像
    100个React最佳实践小技巧

    夕水赞 25阅读 6.5k评论 4

    头像
    前端开发工具

    寒青赞 19阅读 5.2k

    头像
    开发插件集合

    寒青赞 14阅读 3.5k

    头像
    Javascript(turfjs)等值线图绘制

    舍瓦温赞 15阅读 22.5k评论 18

    0 条评论
    得票最新