PTA_数据结构学习与实验指导_题解_2-3.1 海盗分赃

进阶实验2-3.1 海盗分赃

 P 个海盗偷了 D 颗钻石后来到公海分赃，一致同意如下分赃策略：
 首先，P 个海盗通过抽签决定 1 - P 的序号。然后由第 1 号海盗提出一个分配方案（方案应给出每个海盗分得的具体数量），如果能够得到包括 1 号在内的绝对多数（即大于半数）同意，则按照该分配方案执行，否则 1 号将被投入大海喂鲨鱼。而后依次类似地由第 2 号、第 3 号等等海盗提出方案，直到能够获得绝对多数同意的方案出现为止，或者只剩下最后一位海盗，其独占所有钻石。

附带的三个假定：

• “聪明”与“贪婪”假定：每个海盗总能够以本人利益最大化作为行为准则；
• “人性化”假定：在能够取得尽量多钻石的情况下，海盗不会故意致同伙于死地；
• “无偏见”假定：海盗之间没有个人恩怨，分给其他海盗钻石的次序以小序号优先为原则。

 请编写一个程序，给出第 1 号海盗的钻石分配方案中自己分得的钻石数量。
输入格式：
 输入在一行中给出 2 个正整数 D 和 P（3≤P≤D≤100）。
输出格式：
 输出第 1 号海盗的钻石分配方案中自己分得的钻石数量。
输入样例：

10 7   

输出样例1：

6

题目：进阶实验2-3.1 海盗分赃 (25分)

算法分析

 说实话一开始我没看懂什么意思。瞎写了一个只给前 $ \frac {P-1}2$ 个海盗一个人一个钻石的代码...居然还过了几个测试点...
 然后正经分析了一下。发现这题其实就是递推。首先每个海盗考虑利益最大化，所以第 $i$ 个海盗只要在第 $i-1$ 个海盗的方案基础上争取到拿到最少钻石的半数海盗就好了。
 下面拿样例数据模拟一下。

只有一个海盗的时候：

十个都给自己，没有疑问。

两个海盗的时候：

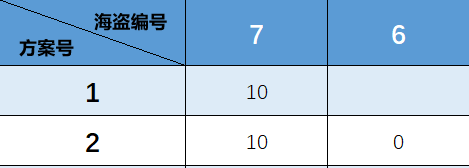
如果6号海盗敢给自己哪怕一个钻石，7号海盗也不会同意。所以6号为了不被喂鱼，只能全部给七号。

三个海盗的时候：

此时，只需要2个人同意5号海盗的分配方案，他就不会被扔下海喂鱼。那么原本6号海盗一个钻石都拿不到，5号只需要给他一个，便能争取到这一票，此时7号海盗给不给都无所谓了，为了利益最大化，必然一个都不给他。

四个海盗的时候：

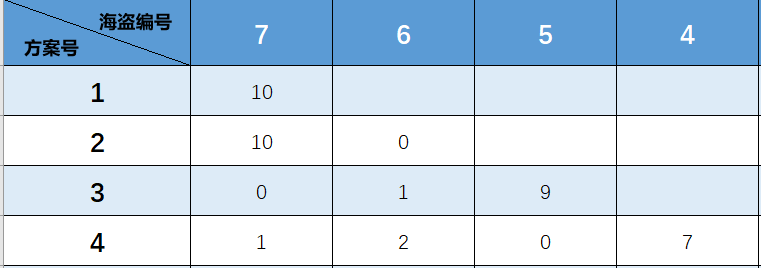
同理。4号海盗需要争取超过半数的同意，即三个人。那么他只要争取到5号海盗给出方案中获利最少的两个人的同意便可。即7号和6号。

递推至七个海盗的情况可得：

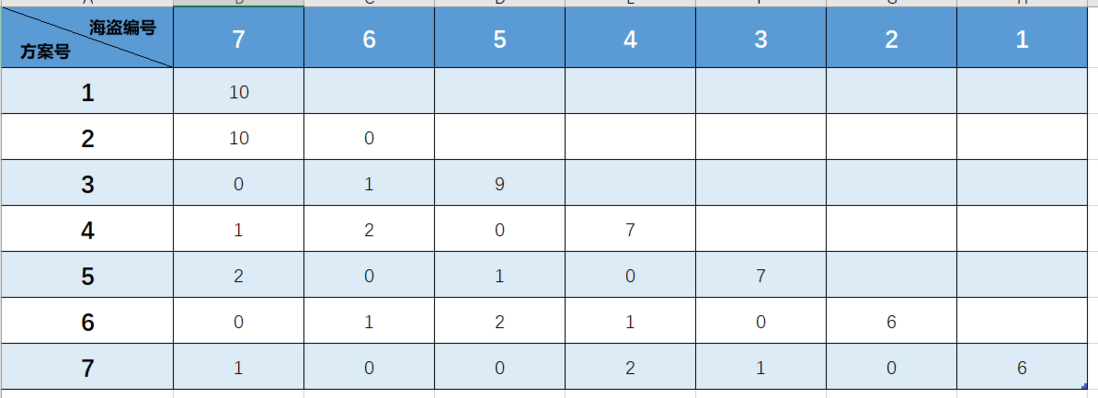
所以我们得到了结论：
 第 $i$ 个海盗的分配方案只与第 $i-1$ 个海盗的方案有关。
 所以我们从两个海盗的情况开始递推，便可得到第P个海盗的方案。
 初始时，编号为 $P$ 的海盗必然是 $D$ 个钻石，编号为 $P-1$ 的海盗 $0$ 个钻石。
 接下来第 $i$ 个海盗，需要在前 $i-1$ 个海盗中争取获利最少的$ \lfloor j=\frac {i}2 \rfloor $个海盗的支持。
 遍历数组，寻找前 $j$ 个小的数， 将它们逐个加一，剩余的数置为 $0$ ，递推这个操作即可。

代码

 非常简洁有力的代码。

#include <stdio.h>
#include <string.h>
int main()
{
    int d, p, a[100]={0}, f[100]={0};
    scanf("%d %d", &d, &p);
    a[--p] = d;
    int n = p-1, min = 101, count = 0, pos = -1, sum = 0;
    while(n--){
        sum = (p-n+1)/2;  /* 需要争取sum个海盗的支持 */ 
        for(int i=0; i<sum; i++){ /* 找寻当前数组未被标记的最小数，标记后+1 */
            for(int j=n+1; j<=p; j++){
                if(a[j] < min && f[j] == 0){
                    min = a[j]; 
                    pos = j;
                }
            }
            a[pos]++;
            f[pos]++;
            min = 101;
        }
        int k = 0; /* 未被+1的数置0 */
        for(int j=n+1; j<=p; j++){
            if(!f[j]) a[j] = 0;
                else k += a[j];
        }
        a[n] = d - k;
        memset(f, 0, sizeof(f));  /* 清空标记数组f */
    }
    printf("%d\n", a[0]);
    return 0;
}

小结

 遇到题目不能想当然了。本次题目不难，又划个水。但是思维方式是通用的。贪心？递推？