Redis-zskiplist(跳表)这种数据结构的思考

1. 跳表数据结构

跳表首先由William Pugh在其1990年的论文《Skip lists: A probabilistic alternative to balanced trees》中提出。由该论文的题目可以知道两点：

跳表是概率型数据结构。
跳表是用来替代平衡树的数据结构。准确来说，是用来替代自平衡二叉查找树（self-balancing BST）的结构。

跳表是对原始的链表进行修改后的变种，利用空间换时间的思想，大幅提高查询性能，跳表支持快速的插入、删除、查找操作。

Redis的zset底层数据结构就是跳表，同样的 JAVA中也有跳表的实现ConcurrentSkipListMap。

如下图，跳表最低层(第一层)是一个拥有跳表所有节点的普通链表，但是原始链表的查询时需要从头到尾依次遍历遇到所有节点，性能较差。

有一个有趣的想法出现了，既然依次遍历太慢，那么如果一次跳过多个节点，比如我想查找节点5，如果可以越过节点1-4，直接访问节点5，那肯定是最完美的。退而求其次，越过节点1-3，直接访问节点4，然后再访问节点5，也是可以接受的。
以此类推，只要可以越过一些不必要访问的节点，减少遍历的节点数目，但从性能角度考虑，都是优于原始链表的，这种思路在希尔排序中也有体现。

当然这样做也会有一个问题，那就是可能会跳过头，越过要访问的节点，这个时候，我们就会发现，如果这个链表是一个有序链表，那么解决起来也很简单，比较一下，越过则直接回头即可。无序链表则。。。洗洗睡吧。。。hash表它不香吗？

为了实现上面的想法，我们就可以给每个节点都维护一组指向其后每一个节点的指针，这样就可以通过任意一个节点，访问到其后的任意一个节点了，但是同时也会发现，所有节点需要维护的指针数目是(n-1)!，这个就太夸张了。

虽然我们的思路是用空间换时间，但是空间和时间都是有成本的，极限小的时间必然需要极限大的空间来换取。一句话，不划算。就像hash表，直接用key的hash code做下标，不香吗？实际却用哈希值取余，然后用拉链法或者探针法，去处理哈希碰撞的问题。原因就是花费巨大的难以实现的空间，相比于换取的时间成本，显得极不划算

然后我们发现，可以折中一点，删掉一些指针，虽然降低查询性能，但是空间成本也可以接受。那么删掉哪些指针呢。因为我们并不知道，那些节点会被更频繁的访问，所以最好的做法就是，删除后，让指针指向的节点可以均匀分布。

是的，一个很自然的想法是我们可以使用随机值，就好像抛硬币，正面朝上，就留下某个节点的指针，反面则删除。

但是，我们在实现中，不可能蠢到生成指针，然后再随机删除，我们只需要生成时候，直接随机生成指针即可。

2. Redis中跳表的实现

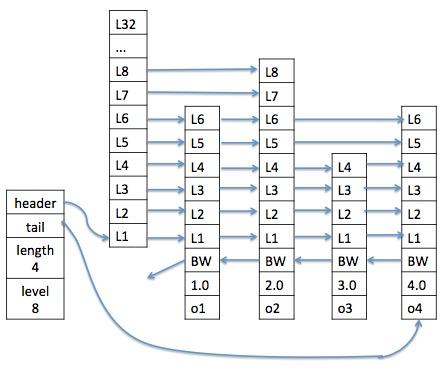
讨论至此，我们已经抓住了跳表这一数据结构的核心，事实上，Redis中跳表的实现就是如此，如下图：

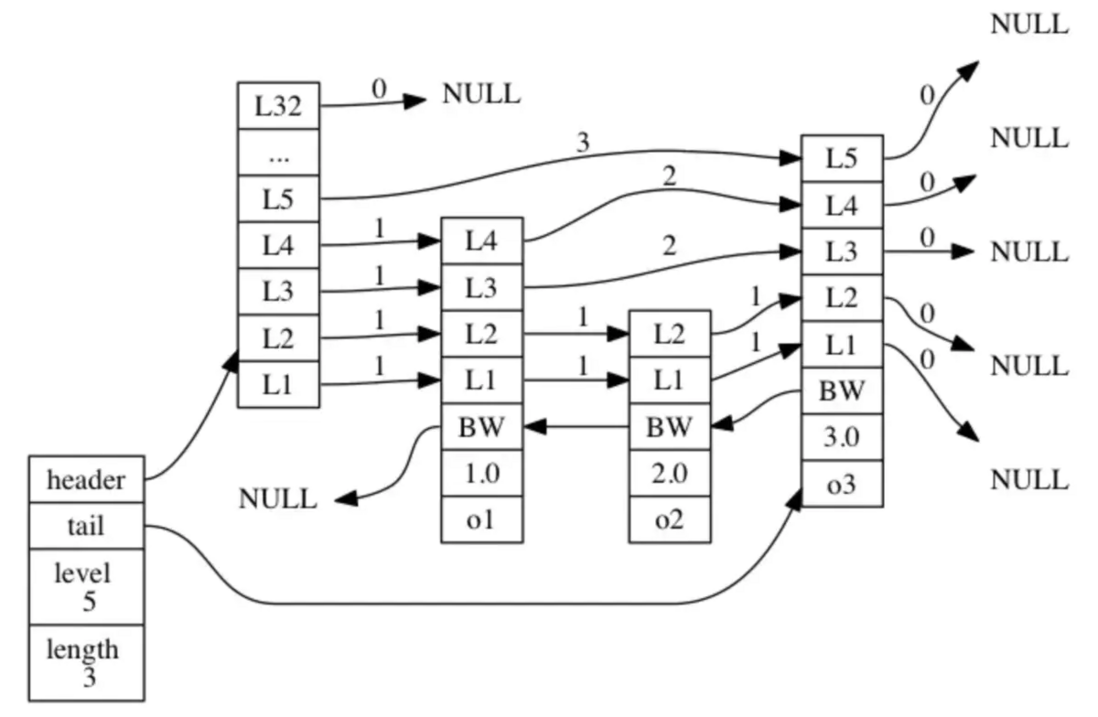
之所以用两张图片是因为，第一张图片指针层级之间对得更齐，更好理解，但是第二张图片才是Redis中跳表数据结构的完美展示。

只不过在细节上做了优化，比如

每个节点上都保存了一个用于指向其后节点的指针数组（即前文所述）；
设置一个指向前一个节点的指针（方便逆向获取数据，如zrevrank、zrevrange）；
创建了一个length和一个level属性用于快速查询跳表的节点数目和指针数组的最大长度；
节点中还会保存前向指针跳过的节点数span，可以用于分页。
最大32层指针，是因为生成指针的期望是1/4，所以2^32个节点中，才会有一个32层指针的节点，32层完全够用。

以下是跳表的数据结构：

//跳表
typedef struct zskiplist {
    // 表头节点和表尾节点
    struct zskiplistNode *header, *tail;
    // 表中节点的数量
    unsigned long length;
    // 表中层数最大的节点的层数
    int level;
} zskiplist;

//跳表节点
typedef struct zskiplistNode {
    // 成员对象
    robj *obj;
    // 分值   作为索引
    double score;
    // 后退指针
    struct zskiplistNode *backward;
    // 节点层结构 数组
    struct zskiplistLevel {
        // 前进指针
        struct zskiplistNode *forward;
        // 该层向前跨越的节点数量
        unsigned int span;
    } level[];
} zskiplistNode;

下图是跳表插入过程的展示：

3. 为什么不用红黑树作为zset底层实现？

其实作者Antirez已经给出了答复：https://news.ycombinator.com/...

They are not very memory intensive. It's up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

zskiplist相较于BST的好处和坏处，大概总结起来有这些：

缺点：

比红黑树占用更多的内存，每个节点的大小取决于该节点的层数
空间局部性较差导致缓存命中率低，感觉上会比红黑树更慢

优点：

实现比红黑树简单
比红黑树更容易扩展，作者之后实现zrank指令时没怎么改动代码。
红黑树插入删除时为了平衡高度需要旋转附近节点，高并发时需要锁。skiplist不需要考虑。
一般用zset的操作都是执行zrange之类的操作，取出一片连续的节点。这些操作的缓存命中率不会比红黑树低。

补充与参考

跳跃列表（Skip List）与其在Redis中的实现详解

《Skip lists: A probabilistic alternative to balanced trees》

Redis 设计与实现

Redis-zskiplist(跳表)这种数据结构的思考