SVM支持向量机笔记1

支持向量机（Support Vector Machine）

这个图 中 好多线都可以把 这两种点分隔开。但是选哪条呢？
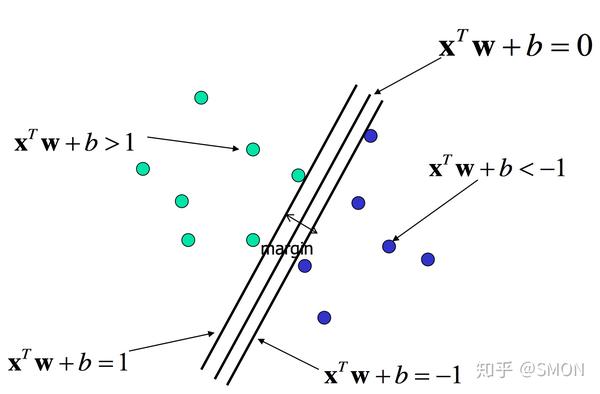
我们直观上肯定是会选中间那个，因为他把两部分数据分的最”开“，拥有最高的容错率。 在这里 最边缘的点其实扮演了很重要的角色 只要能把边界分开，那么自然的 两部分数据也就分开了。”边界“上的点称为”支持向量“。

所以我们的目标是：
1.找到某个超平面（这里是直线），能把两部分数据分开，且他距离支持向量的距离最大。
2.当然这里也要保证支持向量以外的点距离超平面的距离都大于支持向量。

定义

训练数据和标签

一组点和标签（x_i,yi）其中 X是向量，向量可以理解为一组数字。y是标签，表明这个向量所属的类别。

线性模型 （W,b）

W^TX_{+b = 0 (超平面)}

假如x只有二维，那么这个就是普通平面，例如我们常见的线性方程x+y+1 = 0 假如维度很大，那么无法想象出来，就称为超平面。

目的：我们要计算W,b 这样一个超平面的具体的取值

一个训练集的线性可分值得是

对于所有的数据，
如果y=1 则W^TX_{+b >= 0 即在超平面一遍
如果y=-1 则W^TX+b <= 0 即在超平面另一边}

事实1

W^TX_{+b = 0 和 aW^TX+ab = 0 (a是正数)。 为什么要是正数，如果是0的话肯定不行，这就相当于变成了0=0，如果是负数的话，整个平面相当于翻转了一下？ 某个点相对于该超平面的位置会反转。}

事实2 点到屏幕的距离公司

平面w1x+w2y+b= 0，点x0,y0
距离为：d = |w₁x₀+w₂y₀+b| / $\sqrt{w1^2+w2^2}$
这里可以扩充到超平面，见下一部分

向量x0到超平面的距离

距离为：d = |W^TX₀+b| / ||W||

问题简化

我们可以用a去缩放，（w,b）->(aw,ab)
最终使得在支持向量上x0上有：
|W^TX₀+b|| = 1 （这个其实就是使得距离乘以范数等于1 为了方便计算，但是距离实际上并没有改变，因为范数也改变了） 这个时候距离变成了，范数的倒数即：
d = 1/||w||
所以这个时候，我们只关注范数即可，相当于简化了问题的形式
因为我们要找一个超平面，这个超平面尽量的处于两者之间，故我们需要让支持向量距离超平面越大越好，即最大化d，也就是最小化W

既然支持向量都距离为d了 那么支持向量以外的向量，自然要离超平面大于d，即 |W^TX₀+b| >= 1

此时 |W^TX₀+b| >=1 但是W^TX₀+b 其实是有符号的，这要看他在哪一侧。 我们要让两类不同的点在不同的两侧。所以在前边要乘以他们的标签

yi * [W^TX₀+b] >= 1

优化问题(凸优化问题，二次规划问题)

综上svm其实是一个优化问题（二次规划）

最小化

||W||^2 = w1^2 + w2^2 +... + wn^2 （超维平面系数的模的平方）

限制条件

y_i[W^TX_i+b]>=1

二次规划

1.目标函数二次项
2.限制条件是一次性

结论：有一个极小值或者无解。
（有兴趣的可以去看看凸优化理论）