普里姆算法Prim 最小生成树

简介

普里姆算法（Prim's algorithm），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普里姆独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

应用场景

用最小的资源解决更多的问题，非常好用。来看下应用场景

1. 修路问题（修最少的路可以覆盖到更多的村庄）
2. 电线杆，电话线杆
3. 摄像头网络

概念

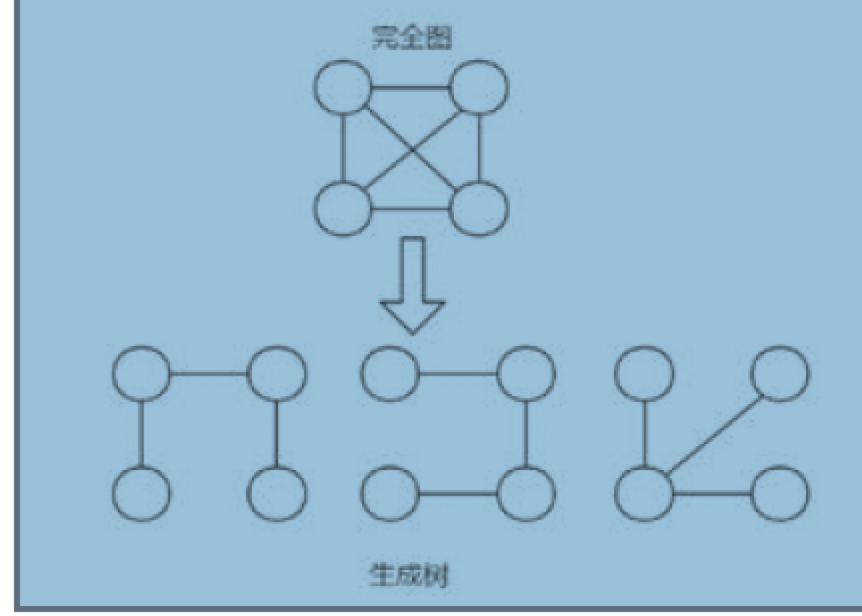
最小生成树

本质就是一个最小生成树问题，简称 MST（Minimum Gost Spanning Tree）。给定一个带权无向图，如何选取一颗生成树，使树上所有边上的权的总和最小，这就是最小生成树。

1. n 个顶点一定有 n-1 条边
2. 包含全部顶点
3. n-1条边一定都在图中

普里姆算法

设 G = (V,E)是连通网，T=(U,D)是最小生成树，V,U 是顶点集合，E,D 是边的集合
若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的 visited[u]=1
若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1
重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有 n-1 条边

案例

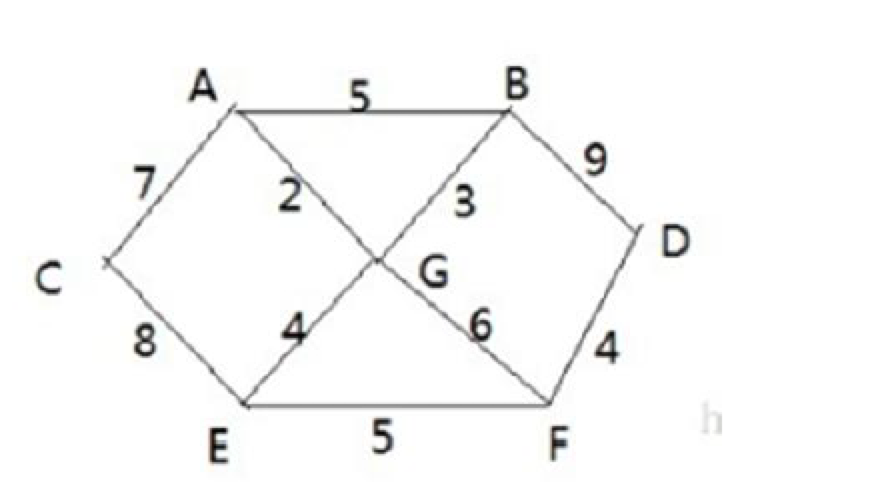
1. 若城市里有7个村庄（A, B, C, D, E, F, G），现在需要修路把7个村庄贯通
2. 各个存在之间的距离用边线（权值）表示，比如 A-B 之间是5公里
3. 怎样修路保证各个村庄之间能连通，并且用最少的资源（里程最小）？

代码实现

生成图，二维数组

假设定义从 A 顶点出发，开始生成

1. 将A 顶点与和 A 相连的顶点比较，选取最小的一个权值并标记
   标记的结果为 A-G(2)
   
2. 使用上一部的结果，从 A, G 顶点出发，再次找到最小的一个权值
   结果为 AG(2)， GB(3)
   
3. AG(2), GB(3),顶点出发，再次选取
   结果为 AG(2), GB(3), GE(4)
   

依次类推

树类

class MGraph {
    public $verxs = 0;
    public $data = [];
    public $weight = [];
    public function __construct($verxs) {
        $this->verxs = $verxs;
        for ($i=0; $i<$verxs; $i++) {
            $this->weight[] = array_fill(0, $verxs, 0);
        }
    }
}

普里姆算法

/**
 * 普里姆算法
 *
 * @param obj $graph 最小生成树
 * @param int $v     出发点
 * @return void
 */
public function prim($graph, $v) {

    $visited = array_fill(0, $graph->verxs, 0);

    // 把当前这个节点标记为已经访问
    $visited[$v] = 1;

    // 记录两个顶点的下标
    $h1 = -1;
    $h2 = -1;

    // 初始化一个大数，在后面的遍历过程中会被替换
    $minWeight = 10000;

    for($k=1; $k<$graph->verxs; $k++) {
        for($i=0; $i<$graph->verxs; $i++) {
            for($j=0; $j<$graph->verxs; $j++) {
                if($visited[$i] == 1 && $visited[$j] == 0 && $graph->weight[$i][$j] > 0 && $graph->weight[$i][$j] < $minWeight) {
                    $minWeight = $graph->weight[$i][$j];
                    $h1 = $i;
                    $h2 = $j;
                }
            }
        }
        // 找到一条边最小
        echo sprintf("边[%s + %s ] = %s", $graph->data[$h1], $graph->data[$h2], $minWeight) . "\n";
        // 讲当前这和节点标记为已经访问
        $visited[$h2] = 1;
        // 重置，标记为最大值
        $minWeight = 10000;
    }
}

复杂度很高，有时间优化一下。

应用变量

$data = ["A", "B", "C", "D", "E", "F", "G"];
$verxs = count($data);
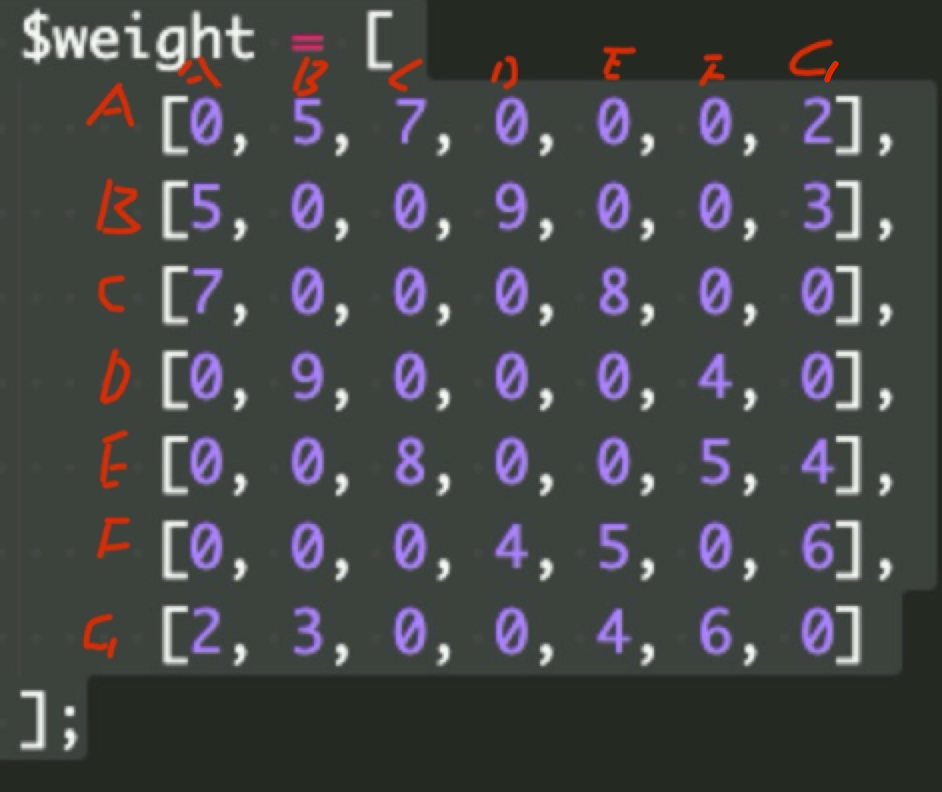
$weight = [
    [0, 5, 7, 0, 0, 0, 2],
    [5, 0, 0, 9, 0, 0, 3],
    [7, 0, 0, 0, 8, 0, 0],
    [0, 9, 0, 0, 0, 4, 0],
    [0, 0, 8, 0, 0, 5, 4],
    [0, 0, 0, 4, 5, 0, 6],
    [2, 3, 0, 0, 4, 6, 0]
];

运行结果

边[A + G ] = 2
边[G + B ] = 3
边[G + E ] = 4
边[E + F ] = 5
边[F + D ] = 4
边[A + C ] = 7

复杂度分析

普里姆算法的运行效率只与连通网中包含的顶点数相关，而和网所含的边数无关。所以普里姆算法适合于解决边稠密的网，该算法运行的时间复杂度为：O(n2)。

参考链接

https://www.jianshu.com/p/c9b...
https://riptutorial.com/zh-TW...
https://github.com/61mon/61mo...（1）.md
http://data.biancheng.net/vie...