一文读懂特征工程

特征工程（feature engineering）：利用领域知识和现有数据，创造出新的特征，用于机器学习算法；可以手动（manual）或自动（automated）。神经网络的自动特征工程，常常不适用于现实中其他的复杂任务。因此，本文主要针对数据挖掘以及传统的机器学习，不会涉及图像识别、自然语言处理等深度学习领域。
俗话说：数据与特征工程决定了模型的上限，改进算法只不过是逼近这个上限而已。
在豆瓣图书频道，搜索‘特征工程’关键词，搜索结果是仅有两本评分在7分以上数据，分别是精通特征工程、特征工程入门与实践

当数据维度有限，那‘特征工程’是非常重要的，但发表这方面文章较少，更没全局化、系统化讲解特征工程理论和实战等，所以我想结合工作经验、相关书籍、优秀文章等总结的一套通用的数据科学-特征工程方法论。
从这 newcommandcolorful{color{red}} colorful{特征理解、特征清洗、特征构造、特征变换} 等维度展开，逐步讲解理论和代码实现等，针对代码实现部分 不能公开公司相关数据，所以选择用泰坦尼克号公开数据。

import pandas as pd
import numpy as np
import seaborn as sns
df_titanic = sns.load_dataset('titanic')

数据字段描述如下：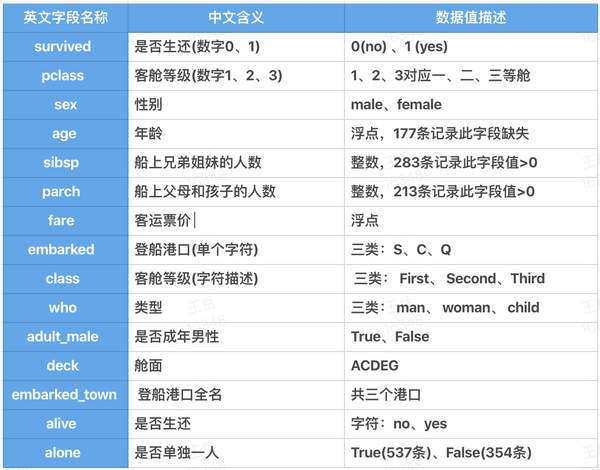

一、特征理解

1.1 区分结构化数据与非结构化数据
如一些以表格形式进行存储的数据，都是结构化数据；而非结构化数据就是一堆数据，类似于文本、报文、日志之类的。
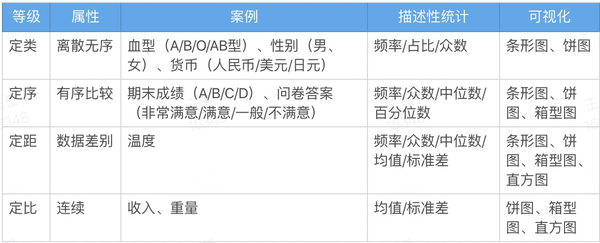
1.2 区分定量和定性数据

• 定量数据：指的是一些数值，用于衡量某件东西的数量；
• 定性数据：指的是一些类别，用于描述某件东西的性质。

二、特征清洗

目标是提高数据质量，降低算法错误建模的风险。
现实的业务建模过程中，数据常常存在各种问题，数据存在不完全的、有噪声的、不一致的等各种情况。而这些带有错误信息的数据会对模型造成不利的影响。
数据清洗过程包括数据对齐、缺失值处理、异常值处理、数据转化等数据处理。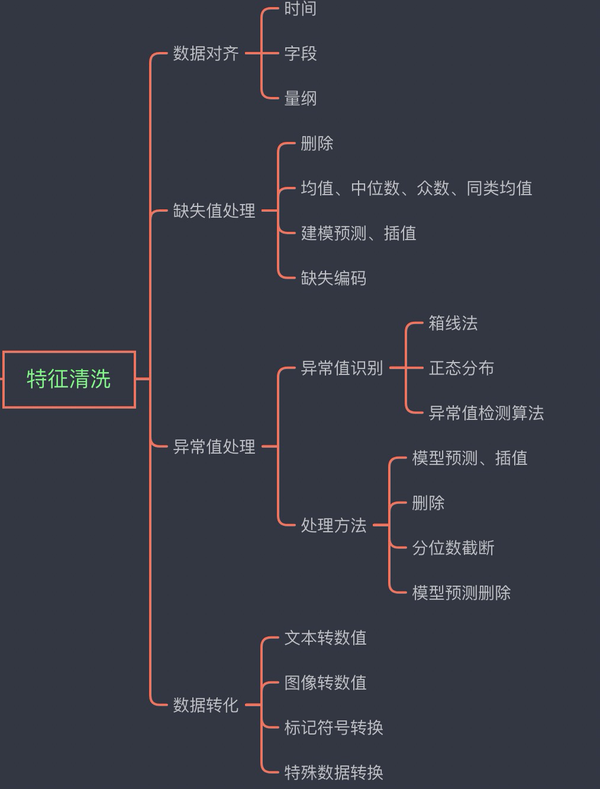

2.1 数据对齐
主要有时间、字段以及相关量纲的对齐。
1) 时间：

• 日期格式不一致【’2019-07-20’、’20190720’、’2019/07/20’、’20/07/2019’】
• 时间戳单位不一致，有的用秒表示，有的用毫秒表示；
• 使用无效时间表示，时间戳使用 0 表示，结束时间戳使用 FFFF 表示。

2) 字段：

• 姓名写了性别，身份证号写了手机号等

3) 量纲：

• 数值类型统一 【如 1、2.0、3.21E3、四】
• 单位统一【如 180cm、1.80m】

2.2 缺失处理

主要包括少量缺失的情况下，考虑不处理或删除缺失数据或者采用均值、中位数、众数、同类均值填充。
当缺失值对模型影响比较大，存在比较多的不缺失数据的情况下，可以采用模型预测或者插值的方式。当缺失值过多时，可以对缺失值进行编码操作。
 对每个字段都计算其缺失值比例，然后按照缺失比例和字段重要性，分别制定策略，可用下图表示：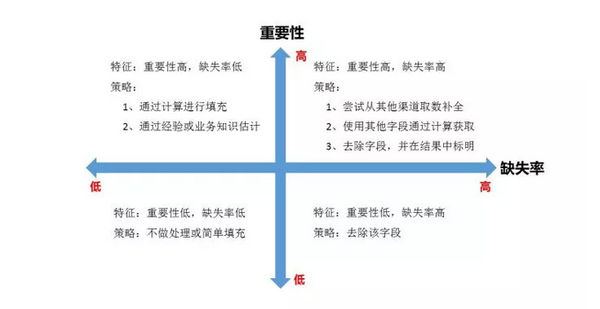

空值汇总分布

df_titanic.isnull().sum()
survived         0
pclass           0
sex              0
age            177
sibsp            0
parch            0
fare             0
embarked         2
class            0
who              0
adult_male       0
deck           688
embark_town      2
alive            0
alone            0

1) 删除元组
将存在遗漏信息属性值的对象（元组，记录）删除，从而得到一个完备的信息表。
优点：
简单易行，在对象有多个属性缺失值、被删除的含缺失值的对象与初始数据集的数据量相比非常小的情况下有效；
不足：
当缺失数据所占比例较大，特别当遗漏数据非随机分布时，这种方法可能导致数据发生偏离，从而引出错误的结论。
代码实现
embark_town 字段 有 2 个空值，可以考虑删除缺失处理下

df_titanic[df_titanic["embark_town"].isnull()]
df_titanic.dropna(axis=0,how='any',subset=['embark_town'],inplace=True)

2) 数据填充
用一定的值去填充空值，从而使信息表完备化。通常基于统计学原理，根据初始数据集中其余对象取值的分布情况来对一个缺失值进行填充。
(a) 人工填充（filling manually）
根据业务知识来进行人工填充。
(b) 特殊值填充（Treating Missing Attribute values as Special values）
将空值作为一种特殊的属性值来处理，它不同于其他的任何属性值。如所有的空值都用“unknown”填充。一般作为临时填充或中间过程。
代码实现

df_titanic['embark_town'].fillna('unknown', inplace=True)

(c) 统计量填充
若缺失率较低（小于 95%）且重要性较低，则根据数据分布的情况进行填充。
常用填充统计量：
平均值：对于数据符合均匀分布，用该变量的均值填补缺失值。
中位数：对于数据存在倾斜分布的情况，采用中位数填补缺失值。
众数：离散特征可使用众数进行填充缺失值。

• 中位数填充

fare：缺失值较多，使用中位数填充。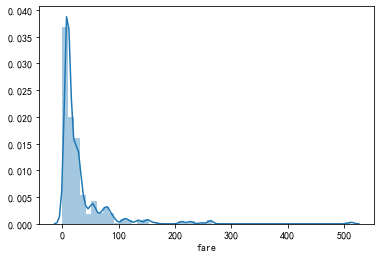

df_titanic['fare'].fillna(df_titanic['fare'].median(), inplace=True) 

• 众数填充

embarked：只有两个缺失值，使用众数填充

df_titanic['embarked'].isnull().sum()
执行结果：2
df_titanic['embarked'].fillna(df_titanic['embarked'].mode(), inplace=True)
df_titanic['embarked'].value_counts()
执行结果：
S    64

• 用 imputer 填充缺失值

imputer 类提供了缺失数值处理的基本策略，比如使用缺失数值所在行或列的均值、中位数、众数来替代缺失值。该类也兼容不同的缺失值编码。
填补缺失值：sklearn.preprocessing.Imputer(missing_values=’NaN’, strategy=’mean’, axis=0, verbose=0, copy=True)
主要参数说明：

missing_values：缺失值，可以为整数或 NaN(缺失值 numpy.nan 用字符串‘NaN’表示)，默认为 NaN strategy：替换策略，字符串，默认用均值‘mean’替换 ① 若为mean时，用特征列的均值替换 ② 若为median时，用特征列的中位数替换 ③ 若为most_frequent时，用特征列的众数替换  axis：指定轴数，默认 axis=0 代表列，axis=1 代表行 copy：设置为 True 代表不在原数据集上修改，设置为 False 时，就地修改，存在如下情况时，即使设置为 False 时，也不会就地修改 ① X不是浮点值数组 ② X是稀疏且missing_values=0 ③ axis=0且X为CRS矩阵 ④ axis=1且X为CSC矩阵 statistics_属性：axis 设置为 0 时，每个特征的填充值数组，axis=1 时，报没有该属性错误

• 同类均值填充

age：根据 sex、pclass 和 who 分组，如果落在相同的组别里，就用这个组别的均值或中位数填充。

df_titanic.groupby(['sex', 'pclass', 'who'])['age'].mean()
执行结果：
 sex     pclass  who 
female  1       child    10.333333
 woman    35.500000
 2       child     6.600000
 woman    32.179688
 3       child     7.100000
 woman    27.854167
male    1       child     5.306667
 man      42.382653
 2       child     2.258889
 man      33.588889
 3       child     6.515000
 man      28.995556
Name: age, dtype: float64
age_group_mean = df_titanic.groupby(['sex', 'pclass', 'who'])['age'].mean().reset_index()
age_group_mean
执行结果：
 sex     pclass  who    age
0    female    1    child    10.333333
1    female    1    woman    35.500000
2    female    2    child    6.600000
3    female    2    woman    32.179688
4    female    3    child    7.100000
5    female    3    woman    27.854167
6    male    1    child    5.306667
7    male    1    man    42.382653
8    male    2    child    2.258889
9    male    2    man    33.588889
10    male    3    child    6.515000
11    male    3    man    28.995556
def select_group_age_median(row):
 condition = ((row['sex'] == age_group_mean['sex']) &
 (row['pclass'] == age_group_mean['pclass']) &
 (row['who'] == age_group_mean['who']))
 return age_group_mean[condition]['age'].values[0]
df_titanic['age'] =df_titanic.apply(
 lambda x: select_group_age_median(x) if np.isnan(x['age']) else x['age'],axis=1)
执行结果：
0      22.000000
1      38.000000
2      26.000000
3      35.000000
4      35.000000
 ... 
886    27.000000
887    19.000000
888    27.854167
889    26.000000
890    32.000000
sns.distplot(df_titani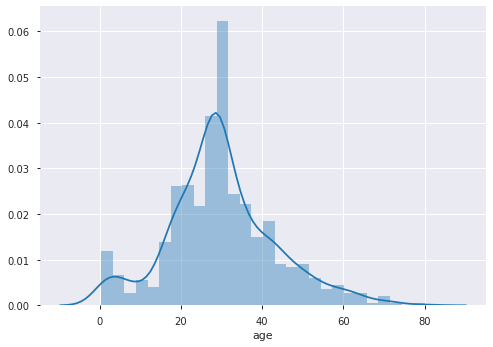

(d) 模型预测填充
使用待填充字段作为 Label，没有缺失的数据作为训练数据，建立分类/回归模型，对待填充的缺失字段进行预测并进行填充。
最近距离邻法（KNN）
先根据欧式距离或相关分析来确定距离具有缺失数据样本最近的 K 个样本，将这 K 个值加权平均/投票来估计该样本的缺失数据。
回归（Regression）
基于完整的数据集，建立回归方程。对于包含空值的对象，将已知属性值代入方程来估计未知属性值，以此估计值来进行填充。当变量不是线性相关时会导致有偏差的估计，常用线性回归。 
代码实现
age：缺失量较大，用 sex、pclass、who、fare、parch、sibsp 六个特征构建随机森林模型，填充年龄缺失值。

df_titanic_age = df_titanic[['age', 'pclass', 'sex', 'who','fare', 'parch', 'sibsp']]
df_titanic_age = pd.get_dummies(df_titanic_age)
df_titanic_age.head()
执行结果为
age    pclass    fare    parch    sibsp    sex_female    sex_male    who_child    who_man    who_woman
0    22.0    3    7.2500    0    1    0    1    0    1    0
1    38.0    1    71.2833    0    1    1    0    0    0    1
2    26.0    3    7.9250    0    0    1    0    0    0    1
3    35.0    1    53.1000    0    1    1    0    0    0    1
4    35.0    3    8.0500    0    0    0    1    0    1    0
# 乘客分成已知年龄和未知年龄两部分
known_age = df_titanic_age[df_titanic_age.age.notnull()]
unknown_age = df_titanic_age[df_titanic_age.age.isnull()]
# y 即目标年龄
y_for_age = known_age['age']
# X 即特征属性值
X_train_for_age = known_age.drop(['age'], axis=1)
X_test_for_age = unknown_age.drop(['age'], axis=1)
from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
rfr.fit(X_train_for_age, y_for_age)
# 用得到的模型进行未知年龄结果预测
y_pred_age = rfr.predict(X_test_for_age)
# 用得到的预测结果填补原缺失数据
df_titanic.loc[df_titanic.age.isnull(), 'age'] = y_pred_age
sns.distplot(df_titanic.age)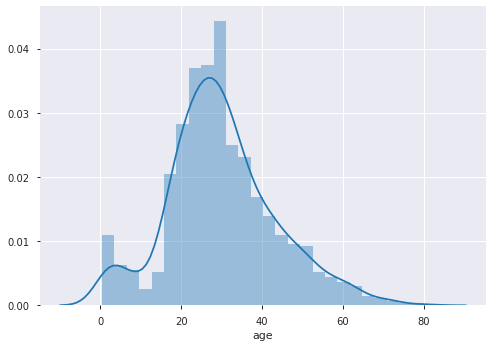

(e) 插值法填充
包括随机插值，多重插补法，热平台插补，拉格朗日插值，牛顿插值等。

• 线性插值法

使用插值法可以计算缺失值的估计值，所谓的插值法就是通过两点（x0，y0），（x1，y1）估计中间点的值，假设 y=f(x)是一条直线，通过已知的两点来计算函数 f(x)，然后只要知道 x 就能求出 y，以此方法来估计缺失值。
.interpolate(method = 'linear', axis) 方法将通过 linear 插值使用沿着给定 axis 的值替换 NaN 值, 这个差值也就是前后或者上下的中间值

df_titanic['fare'].interpolate(method = 'linear', axis = 0)

同时，也可用行值插入

df_titanic['fare'].interpolate(method = 'linear', axis = 1)

代码实现

df_titanic['fare'].interpolate()

• 多重插补（Multiple Imputation）

多值插补的思想来源于贝叶斯估计，认为待插补的值是随机的，它的值来自于已观测到的值。具体实践上通常是估计出待插补的值，然后再加上不同的噪声，形成多组可选插补值。根据某种选择依据，选取最合适的插补值。
多重插补方法分为三个步骤：
Step1：为每个空值产生一套可能的插补值，这些值反映了无响应模型的不确定性；
每个值都可以被用来插补数据集中的缺失值，产生若干个完整数据集合；
Step2：每个插补数据集合都用针对完整数据集的统计方法进行统计分析；
Step3：对来自各个插补数据集的结果，根据评分函数进行选择，产生最终的插补值。
(f) 哑变量填充
若变量是离散型，且不同值较少，可转换成哑变量，例如性别 SEX 变量，存在 male，fameal，NA 三个不同的值，可将该列转换成 IS_SEX_MALE、IS_SEX_FEMALE、IS_SEX_NA。若某个变量存在十几个不同的值，可根据每个值的频数，将频数较小的值归为一类’other’，降低维度。此做法可最大化保留变量的信息。
代码实现

sex_list = ['MALE', 'FEMALE', np.NaN, 'FEMALE', 'FEMALE', np.NaN, 'MALE']
df = pd.DataFrame({'SEX': sex_list})
display(df)
df.fillna('NA', inplace=True)
df = pd.get_dummies(df['SEX'],prefix='IS_SEX')
display(df)
# 原始数据
 SEX
0    MALE
1    FEMALE
2    NaN
3    FEMALE
4    FEMALE
5    NaN
6    MALE
# 填充后
 IS_SEX_FEMALE     IS_SEX_MALE    IS_SEX_NA
0    0                 1                0
1    1                 0                0
2    0                 0                1
3    1                 0                0
4    1                 0                0
5    0                 0                1
6    0                 1 

(g) 当特征值缺失超过 80%以上，建议删除【或变成是否变量】，容易影响模型效果

df_titanic.drop(["deck"],axis=1)

2.3 异常处理：
1) 异常值识别

• 箱线法

sns.catplot(y="fare",x="survived", kind="box", data=df_titanic,palette="Set2");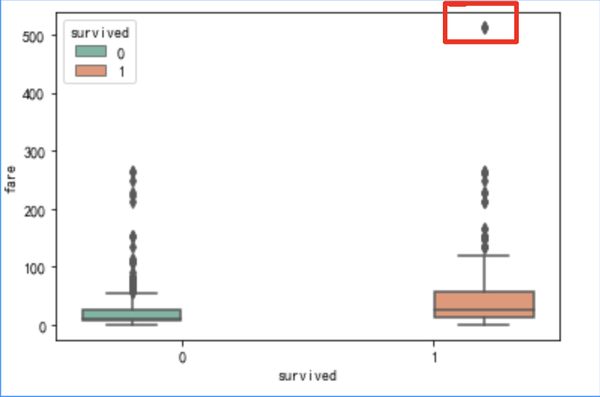

• 正态分布

sns.distplot(df_titanic.age)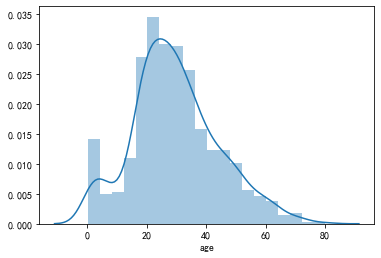

• 异常值检测方法

(a) 基于统计分析
通常用户用某个统计分布对数据点进行建模，再以假定的模型，根据点的分布来确定是否异常。
如通过分析统计数据的散度情况，即数据变异指标，对数据的分布情况有所了解，进而通过数据变异指标来发现数据中的异常点数据。
常用的数据变异指标有极差、四分位数间距、均差、标准差、变异系数等等，如变异指标的值大表示变异大、散布广；值小表示离差小，较密集。
譬如最大最小值可以用来判断这个变量的取值是否超过了合理的范围，如客户的年龄为-20 岁或 200 岁，为异常值。
(b) 3σ原则
若数据存在正态分布，在 3σ原则下，异常值为一组测定值中与平均值的偏差超过3倍标准差的值。如果数据服从正态分布，距离平均值3σ之外的值出现的概率为P(|x - μ| > 3σ) <= 0.003，属于极个别的小概率事件。如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。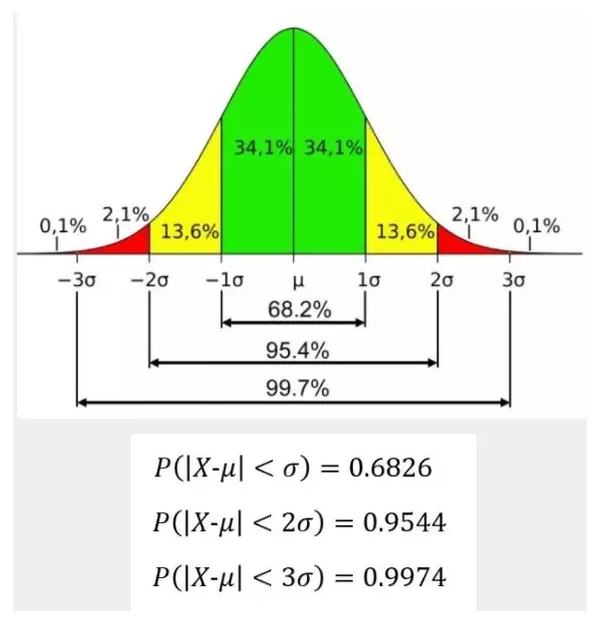

(c) 箱线图分析
箱线图提供了识别异常值的一个标准：如果一个值小于 Q1-1.5IQR 或大于 Q3+1.5IQR 的值，则被称为异常值。
Q1 为下四分位数，表示全部观察值中有四分之一的数据取值比它小；
Q4 为上四分位数，表示全部观察值中有四分之一的数据取值比它大；
IQR 为四分位数间距，是上四分位数 Q1 与下四分位数 Q3 的差值，包含了全部观察值的一半。
箱型图判断异常值的方法以四分位数和四分位距为基础，四分位数具有鲁棒性：25%的数据可以变得任意远并且不会干扰四分位数，所以异常值不能对这个标准施加影响。因此箱型图识别异常值比较客观，在识别异常值时有一定的优越性。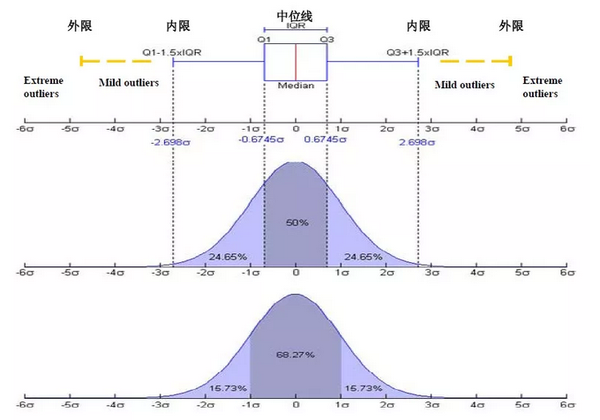 

(d) 基于模型检测
首先建立一个数据模型，异常是那些同模型不能完美拟合的对象；如果模型是簇的集合，则异常是不显著属于任何簇的对象；在使用回归模型时，异常是相对远离预测值的对象。
优点：
有坚实的统计学理论基础，当存在充分的数据和所用的检验类型的知识时，这些检验可能非常有效。
缺点：
对于多元数据，可用的选择少一些，并且对于高维数据，这些检测可能性很差。
(e) 基于距离
基于距离的方法是基于下面这个假设：即若一个数据对象和大多数点距离都很远，那这个对象就是异常。通过定义对象之间的临近性度量，根据距离判断异常对象是否远离其他对象，主要使用的距离度量方法有绝对距离(曼哈顿距离)、欧氏距离和马氏距离等方法。
优点：
基于距离的方法比基于统计类方法要简单得多；
因为为一个数据集合定义一个距离的度量要比确定数据集合的分布容易的多。
缺点：
基于邻近度的方法需要 O(m2)时间，大数据集不适用；
该方法对参数的选择也是敏感的；
不能处理具有不同密度区域的数据集，因为它使用全局阈值，不能考虑这种密度的变化。
(f) 基于密度
考察当前点周围密度，可以发现局部异常点，离群点的局部密度显著低于大部分近邻点，适用于非均匀的数据集。
优点：
给出了对象是离群点的定量度量，并且即使数据具有不同的区域也能够很好的处理。
缺点：
与基于距离的方法一样，这些方法必然具有 O(m2)的时间复杂度。
对于低维数据使用特定的数据结构可以达到 O(mlogm)；
参数选择困难。
虽然算法通过观察不同的 k 值，取得最大离群点得分来处理该问题，但是，仍然需要选择这些值的上下界。
(g) 基于聚类
对象是否被认为是异常点可能依赖于簇的个数（如 k 很大时的噪声簇）。该问题也没有简单的答案。一种策略是对于不同的簇个数重复该分析。另一种方法是找出大量小簇，其想法是：
较小的簇倾向于更加凝聚；
如果存在大量小簇时一个对象是异常点，则它多半是一个真正的异常点。
不利的一面是一组异常点可能形成小簇而逃避检测。
优点：
基于线性和接近线性复杂度（k 均值）的聚类技术来发现离群点可能是高度有效的；
簇的定义通常是离群点的补，因此可能同时发现簇和离群点。
缺点:
产生的离群点集和它们的得分可能非常依赖所用的簇的个数和数据中离群点的存在性；
聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大。
(h) 基于邻近度的异常点检测
一个对象是异常的，如果它远离大部分点。这种方法比统计学方法更一般、更容易使用，因为确定数据集的有意义的邻近性度量比确定它的统计分布更容易。一个对象的异常点得分由到它的 k-最近邻的距离给定。异常点得分对 k 的取值高度敏感。如果 k 太小（例如 1），则少量的邻近异常异常点可能导致较异常低的异常点得分；如果 K 太大，则点数少于 k 的簇中所有的对象可能都成了异常异常点。为了使该方案对于 k 的选取更具有鲁棒性，可以使用 k 个最近邻的平均距离。
优点：
简单
缺点:
基于邻近度的方法需要 O(m2)时间，大数据集不适用；
该方法对参数的选择也是敏感的；
不能处理具有不同密度区域的数据集，因为它使用全局阈值，不能考虑这种密度的变化。
总结：
在数据处理阶段将离群点作为影响数据质量的异常点考虑，而不是作为通常所说的异常检测目标点，一般采用较为简单直观的方法，结合箱线图和 MAD 的统计方法判断变量的离群点。

 sns.scatterplot(x="fare", y="age", hue="survived",data=df_titanic,palette="Set1")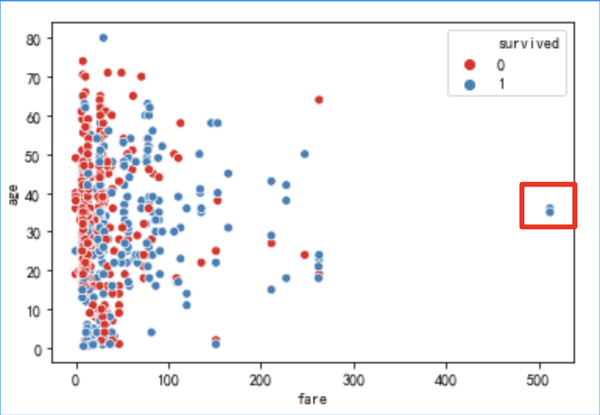

2) 处理方法
对异常值处理，需要具体情况具体分析，异常值处理的方法常用有四种：

• 删除含有异常值的记录；
• 某些筛选出来的异常样本是否真的是不需要的异常特征样本，最好找懂业务的再确认一下，防止我们将正常的样本过滤掉了。
• 将异常值视为缺失值，交给缺失值处理方法来处理；
• 使用均值/中位数/众数来修正；
• 不处理。

三、特征构造

3.1 特征构造

目标是增强数据表达，添加先验知识。
如果我们对变量进行处理之后，效果仍不是非常理想，就需要进行特征构建了，也就是衍生新变量。 

3.3.1 统计量构造：

1) 基于业务规则、先验知识等构建新特征
2) 四分位数、中位数、平均值、标准差、偏差、偏度、偏锋、离散系统
3) 构造长、短期统计量（如 周、月）
4) 时间衰减（越靠近观测权重值高）

• 年龄分段：child、young、midlife、old

def age_bin(x):
 if x <= 18:
 return 'child'
 elif x <= 30:
 return 'young'
 elif x <= 55:
 return 'midlife'
 else:
 return 'old'
df_titanic['age_bin'] = df_titanic['age'].map(age_bin)
df_titanic['age_bin'].unique()
执行结果：
array(['young', 'midlife', 'child', 'old'], dtype=object)

• 抽取 title 特征

df_titanic['title'] = df_titanic['name'].map(
 lambda x: x.split(',')[1].split('.')[0].strip())
 
df_titanic['title'].value_counts()
执行结果：
Mr              757
Miss            260
Mrs             197
Master           61
Rev               8
Dr                8
Col               4
Ms                2
Major             2
Mlle              2
Dona              1
Sir               1
Capt              1
Don               1
Lady              1
Mme               1
the Countess      1
Jonkheer          1
# 再根据这些 title 细分，是官员，还是皇室，还是女士、先生、小姐
df_titanic['title'].unique()
执行结果：
array(['Mr', 'Mrs', 'Miss', 'Master', 'Don', 'Rev', 'Dr', 'Mme', 'Ms',
 'Major', 'Lady', 'Sir', 'Mlle', 'Col', 'Capt', 'the Countess',
 'Jonkheer', 'Dona'], dtype=object)
 
title_dictionary = {
 "Mr": "Mr",
 "Mrs": "Mrs",
 "Miss": "Miss",
 "Master": "Master",
 "Don": "Royalty",
 "Rev": "Officer",
 "Dr": "Officer",
 "Mme": "Mrs",
 "Ms": "Mrs",
 "Major": "Officer",
 "Lady": "Royalty",
 "Sir": "Royalty",
 "Mlle": "Miss",
 "Col": "Officer",
 "Capt": "Officer",
 "the Countess": "Royalty",
 "Jonkheer": "Royalty",
 "Dona": 'Mrs'
}
df_titanic['title'] = df_titanic['title'].map(title_dictionary)
df_titanic['title'].value_counts()
执行结果：
Mr         757
Miss       262
Mrs        201
Master      61
Officer     23
Royalty      5

• 抽取家庭规模

df_titanic['family_size'] = df_titanic['sibsp'] + df_titanic['parch'] + 1
df_titanic['family_size'].head()
执行结果：
0    2
1    2
2    1
3    2
4    1

3.3.2 周期值：

1) 前n个周期/天/月/年的周期值，如过去5天分位数、平均值等
2) 同比/环比 

3.3.3 数据分桶：

1) 等频、等距分桶

(a) 自定义分箱
指根据业务经验或者常识等自行设定划分的区间，然后将原始数据归类到各个区间中。
(b) 等距分箱
按照相同宽度将数据分成几等份。
从最小值到最大值之间,均分为 N 等份, 这样, 如果 A,B 为最小最大值, 则每个区间的长度为 W=(B−A)/N , 则区间边界值为A+W,A+2W,….A+(N−1)W 。这里只考虑边界，每个等份里面的实例数量可能不等。
缺点是受到异常值的影响比较大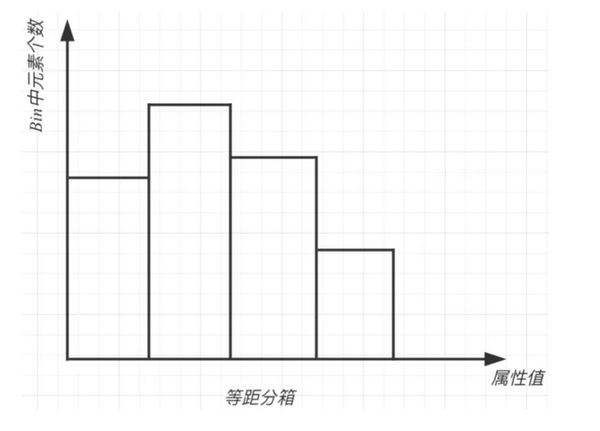

(c) 等频分箱
将数据分成几等份，每等份数据里面的个数是一样的。
区间的边界值要经过选择,使得每个区间包含大致相等的实例数量。比如说 N=10 ,每个区间应该包含大约10%的实例。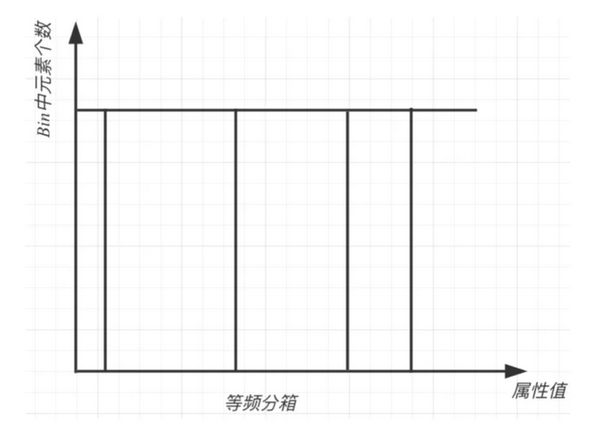

• 数值变量分箱

# qcut 等频率分箱
df_titanic['fare_bin'], bins = pd.qcut(df_titanic['fare'], 5, retbins=True)
df_titanic['fare_bin'].value_counts()
(7.854, 10.5]        184
(21.679, 39.688]     180
(-0.001, 7.854]      179
(39.688, 512.329]    176
(10.5, 21.679]       172
bins #array([  0.    ,   7.8542,  10.5   ,  21.6792,  39.6875, 512.3292])
def fare_cut(age):
 if age <=  7.8958:
 return 0
 if age <= 10.5:
 return 1
 if age <= 21.6792:
 return 2
 if age <=  39.6875:
 return 3
 return 4
 
df_titanic['fare_bin'] = df_titanic['fare'].map(fare_cut)
# cut 等距离分箱
bins = [0, 12, 18, 65, 100]
pd.cut(df_titanic['age'], bins).value_counts

2) Best-KS分桶

1.将特征值值进行从小到大的排序。
2.计算出KS最大的那个值，即为切点，记为D。然后把数据切分成两部分。
3.重复步骤2，进行递归，D左右的数据进一步切割。直到KS的箱体数达到我们的预设阈值即可。
4.连续型变量：分箱后的KS值<=分箱前的KS值
5.分箱过程中，决定分箱后的KS值是某一个切点，而不是多个切点的共同作用。这个切点的位置是原始KS值最大的位置。
 注：代码实现请从网上查阅
3) 卡方分桶
自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验：具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
基本思想
对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。
实现步骤
Step 1：预先定义一个卡方的阈值；
Step 2：初始化；根据要离散的属性对实例进行排序，每个实例属于一个区间；
Step 3：合并区间；
计算每一对相邻区间的卡方值；
将卡方值最小的一对区间合并；
Aij：第i区间第j类的实例的数量；Eij：Aij的期望频率（=(Ni*Cj)/N），N是总样本数，Ni是第i组的样本数，Cj是第j类样本在全体中的比例；
阈值的意义
类别和属性独立时,有90%的可能性,计算得到的卡方值会小于4.6。大于阈值4.6的卡方值就说明属性和类不是相互独立的，不能合并。如果阈值选的大,区间合并就会进行很多次,离散后的区间数量少、区间大。
注意

ChiMerge算法推荐使用0.90、0.95、0.99置信度，最大区间数取10到15之间； 也可以不考虑卡方阈值，此时可以考虑最小区间数或者最大区间数。 指定区间数量的上限和下限，最多几个区间,最少几个区间； 对于类别型变量，需要分箱时需要按照某种方式进行排序。
代码实现
https://github.com/tatsumiw/C...

3) 最小熵法分箱

需要使总熵值达到最小，也就是使分箱能够最大限度地区分因变量的各类别。
熵是信息论中数据无序程度的度量标准，提出信息熵的基本目的是找出某种符号系统的信息量和冗余度之间的关系，以便能用最小的成本和消耗来实现最高效率的数据存储、管理和传递。
数据集的熵越低，说明数据之间的差异越小，最小熵划分就是为了使每箱中的数据具有最好的相似性。给定箱的个数，如果考虑所有可能的分箱情况，最小熵方法得到的箱应该是具有最小熵的分箱。

3.3.4 特征组合

注：有限考虑强特征维度
1) 离散+离散：笛卡尔积
2) 离散+连续：连续特征分桶后进行笛卡尔积或基于类别特征 group  by，类似于聚类特征构造
3) 连续+连续：加减乘除，二阶差分等

• 多项式生成新特征【针对连续值】

df_titanic_numerical = df_titanic[['age','sibsp','parch','fare','family_size']]
df_titanic_numerical.head()
执行结果：
age    sibsp    parch    fare    family_size
0    22.0    1    0    7.2500    2
1    38.0    1    0    71.2833    2
2    26.0    0    0    7.9250    1
3    35.0    1    0    53.1000    2
4    35.0    0    0    8.0500    1
# 扩展数值特征
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)
df_titanic_numerical_poly = poly.fit_transform(df_titanic_numerical)
pd.DataFrame(df_titanic_numerical_poly, columns=poly.get_feature_names()).hea

查看下衍生新变量后的相关性情况，颜色越深相关性越大：

sns.heatmap(pd.DataFrame(df_titanic_numerical_poly, columns=poly.get_feature_names()).corr())

3.4 特征选择

目标是降低噪声，平滑预测能力和计算复杂度，增强模型预测性能
当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。
通常来说，从两个方面考虑来选择特征：

• 特征是否发散：如果一个特征不发散，例如方差接近于 0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
• 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。

根据特征选择的形式又可以将特征选择方法分为 3 种：

• Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数来选择特征。
• Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征或者排除若干特征。
• Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于 Filter 方法，但是是通过训练来确定特征的优劣。  我们使用 sklearn 中的 feature_selection 库来进行特征选择。

3.4.1 过滤式

1) 方差过滤
这是通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么，都要优先消除方差为 0 的特征。VarianceThreshold 有重要参数 threshold，表示方差的阈值，表示舍弃所有方差小于 threshold 的特征，不填默认为 0，即删除所有的记录都相同的特征。

from sklearn.feature_selection import VarianceThreshold
variancethreshold = VarianceThreshold() #实例化，默认方差为 0.方差<=0 的过滤掉
df_titanic_numerical = df_titanic[['age','sibsp','parch','fare','family_size']]
X_var = variancethreshold.fit_transform(df_titanic_numerical)    #获取删除不合格特征后的新特征矩阵
variancethreshold.variances_
array([ 79.58,1.21467827,0.64899903,512.3292,2.60032675])
del_list = df_titanic_numerical.columns[variancethreshold.get_support()==0].to_list()  #获得删除

然 而，如果我们知道我们需要多少个特征，方差也可以帮助我们将特征选择一步到位。
比如说，我们希望留下一半的特征，那可以设定一个让特征总数减半的方差阈值，只要找到特征方差的中位数，再将这个中位数作为参数 threshold 的值输入就好了：

df_titanic_numerical_fsvar = VarianceThreshold(np.median(df_titanic_numerical.var().values)).fit_transform(df_titanic_numerical)

当特征是二分类时，特征的取值就是伯努利随机变，假设 p=0.8，即二分类特征中某种分类占到 80%以上的时候删除特征

X_bvar = VarianceThreshold(.8 * (1 - .8)).fit_transform(df_titanic_numerical) 
X_bvar.shape
执行结果：
(891, 5)

2) 卡方过滤
卡方检验，专用于分类算法，捕捉相关性 追求 p 小于显著性水平的特征
卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。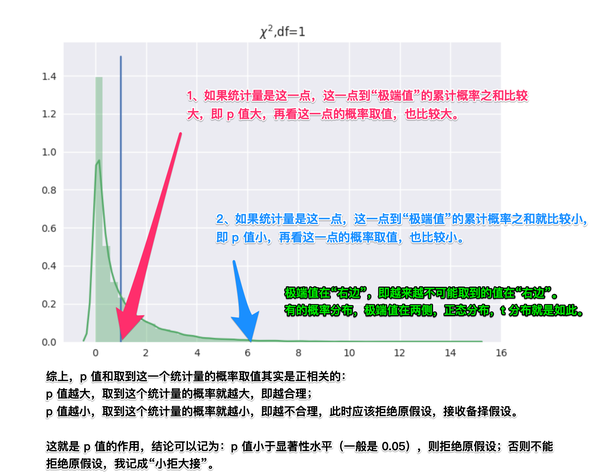

卡方检验类 feature_selection.chi2 计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名

df_titanic_categorical = df_titanic[['sex', 'class', 'embarked', 'who',  'age_bin','adult_male','alone','fare_bin']]
df_titanic_numerical = df_titanic[['age','sibsp','parch','fare','family_size','pclass']]
df_titanic_categorical_one_hot = pd.get_dummies(
 df_titanic_categorical,
 columns=['sex', 'class', 'embarked', 'who',  'age_bin','adult_male','alone','fare_bin'],
 drop_first=True)
df_titanic_combined = pd.concat([df_titanic_numerical,df_titanic_categorical_one_hot],axis=1)
y = df_titanic['survived']
X = df_titanic_combined.iloc[:,1:]
from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest
chi_value, p_value = chi2(X,y)
#根据 p 值，得出 k 值
k = chi_value.shape[0] - (p_value > 0.05).sum()  #要保留的特征的数量 14
#根据卡方值，选择前几特征,筛选后特征
X_chi = SelectKBest(chi2, k=14).fit_transform(X, y)
X_chi.shape
(89

3)  F 检验
只能捕捉线性相关性 要求数据服从正态分布，追求 P 值小于显著性水平特征。
F 检验，又称 ANOVA，方差齐性检验，是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类，因此包含 feature_selection.f_classif（F 检验分类）和 feature_selection.f_regression（F 检验回归）两个类。其中 F 检验分类用于标签是离散型变量的数据，而 F 检验回归用于标签是连续型变量的数据。
F 检验的本质是寻找两组数据之间的线性关系，其原假设是”数据不存在显著的线性关系“。

from sklearn.feature_selection import f_classif
f_value, p_value = f_classif(X,y)
#根据 p 值，得出 k 值
k = f_value.shape[0] - (p_value > 0.05).sum()
#筛选后特征
X_classif = SelectKBest(f_classif, k=14).fit_transform(X, y)

4)  互信息法
可以捕捉任何相关性 不能用于稀疏矩阵，追求互信息大于 0 的特征
互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法。和 F 检验相似，它既可以做回归也可以做分类，并且包含两个类:
feature_selection.mutual_info_classif（互信息分类）feature_selection.mutual_info_regression（互信息回归）
这两个类的用法和参数都和 F 检验一模一样，不过 互信息法比 F 检验更加强大，F 检验只能够找出线性关系，而互信息法可以找出任意关系。 互信息法不返回 p 值或 F 值类似的统计量，它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为 0 则表示两个变量独立，为 1 则表示两个变量完全相关。

from sklearn.feature_selection import mutual_info_classif as MIC
#互信息法
mic_result = MIC(X,y)   #互信息量估计
k = mic_result.shape[0] - sum(mic_result <= 0)    #16
X_mic = SelectKBest(MIC, k=16).fit_transform(X, y)
X_mic.shape
(891, 16)

3.4.2 包裹式

1)  递归特征消除法
递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用 feature_selection 库的 RFE 类来选择特征的代码如下：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
#递归特征消除法，返回特征选择后的数据
#参数 estimator 为基模型
#参数 n_features_to_select 为选择的特征个数
X_ref = RFE(estimator=LogisticRegression(), n_features_to_select=10).fit_transform(X, y)

2) 重要性评估

from sklearn.ensemble import ExtraTreesClassifier
# feature extraction
model = ExtraTreesClassifier()
model.fit(X, y)
print(model.feature_importances_)
feature=list(zip(X.columns,model.feature_importances_))
feature=pd.DataFrame(feature,columns=['feature','importances'])
feature.sort_values(by='importances',ascending=False).head(20)
feature    importances
2    fare    0.227659
15    adult_male_True    0.130000
10    who_man    0.108939
5    sex_male    0.078065
11    who_woman    0.059090
7    class_Third    0.055755
4    pclass    0.048733
3    family_size    0.038347
0    sibsp    0.035489
9    embarked_S    0.029512
1    parch    0.023778
20    fare_bin_(39.688, 512.329]    0.022985
14    age_bin_young    0.021404
12    age_bin_midlife    0.019379
6    class_Second    0.019301
17    fare_bin_(7.854, 10.5]    0.016448
19    fare_bin_(21.679, 39.688]    0.016006
18    fare_bin_(10.5, 21.679]    0.014871
16    alone_True    0.013093
13    age_bin_old    0.0112

3) 排列重要性评估
优点：快速计算；易于使用和理解；特征重要性度量的属性；追求特征稳定性
原理：在训练机器学习模型之后计算置换重要性。这种方法在向模型提出假设，如果在保留目标和所有其他列的同时随机打乱一列验证集特征数据，对预测机器学习模型的准确性的影响程度。对于一个具有高度重要性的特征，random-reshuffle会对机器学习模型预测的准确性造成更大的损害。
结果解读：每一行的第一个数字表示模型性能(例子中用的是准确率)衰减了多少，±后面的数字表示多次打乱的标准差。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import eli5
from eli5.sklearn import PermutationImportance
my_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)
perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())

3.4.3 嵌入式

1)  基于惩罚项的特征选择法
使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。
使用 feature_selection 库的 SelectFromModel 类结合带 L1 惩罚项的逻辑回归模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#带 L1 和 L2 惩罚项的逻辑回归作为基模型的特征选择,这个设置带 L1 惩罚项的逻辑回归作为基模型的特征选择
lr = LogisticRegression(solver='liblinear',penalty="l1", C=0.1)
X_sfm = SelectFromModel(lr).fit_transform(X, y)
X_sfm.shape
(891, 7

使用 feature_selection 库的 SelectFromModel 类结合 SVM 模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.svm import LinearSVC
lsvc = LinearSVC(C=0.01,penalty='l1',dual=False).fit(X, y)
model = SelectFromModel(lsvc,prefit=True)
X_sfm_svm = model.transform(X)
X_sfm_svm.shape
(891, 7

2) 基于树模型
​    树模型中 GBDT 也可用来作为基模型进行特征选择，使用 feature_selection 库的 SelectFromModel 类结合 GBDT 模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
#GBDT 作为基模型的特征选择
gbdt = GradientBoostingClassifier()
X_sfm_gbdt = SelectFromModel(gbdt).fit_transform(X, y)
X_sfm_gbdt.shape
(891, 5)

总结一下，有几点做特征选择的方法经验：
（1）如果特征是分类变量，那么可以从 SelectKBest 开始，用卡方或者基于树的选择器来选择变量；
（2）如果特征是定量变量，可以直接用线性模型和基于相关性的选择器来选择变量；
（3）如果是二分类问题，可以考虑使用 SelectFromModel 和 SVC；
（4）在进行特征选择前，还是需要做一下 EDA。

四、特征变换

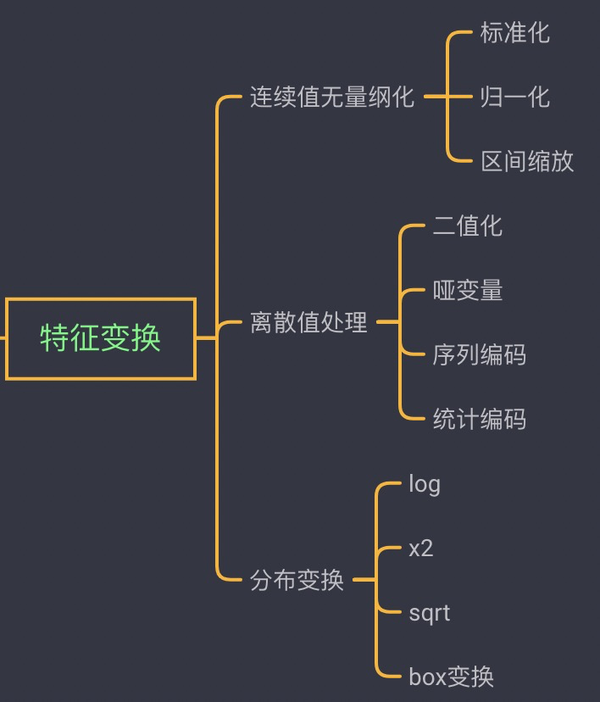
1) 标准化（Standardization）

转换为 Z-score，使数值特征列的算数平均为 0，方差（以及标准差）为 1。不免疫 outlier。 
注：如果数值特征列中存在数值极大或极小的 outlier（通过 EDA 发现），应该使用更稳健（robust）的统计数据：用中位数而不是算术平均数，用分位数（quantile）而不是方差。这种标准化方法有一个重要的参数：（分位数下限，分位数上限），最好通过 EDA 的数据可视化确定。免疫 outlier。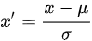

from sklearn.preprocessing import StandardScale
#标准化模型训练
Stan_scaler = StandardScaler()
Stan_scaler.fit(x)
x_zscore = Stan_scaler.transform(x)
x_test_zscore = Stan_scaler.transform(x_test)
joblib.dump(Stan_scaler,'zscore.m')  #写入文件

2)  归一化（Normalization）

把每一行数据归一化，使之有 unit norm，norm 的种类可以选 l1、l2 或 max。不免疫 outlier。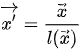 

，其中 iota 表示 norm 函数。 

3)  区间缩放（scaling）

将一列的数值，除以这一列的最大绝对值。
MinMaxScaler：线性映射到 [ 0，1 ] ，不免疫 outlier。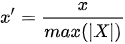 

MaxAbsScaler：线性映射到 [ -1，1 ] ，不免疫 outlier。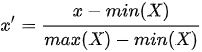 

from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
min_max_scaler.fit_transform(x)
x_minmax = min_max_scaler.transform(x)
x_test_minmax = min_max_scaler.transform(x_test)
joblib.dump(min_max_scaler,'min_max_scaler.m')  #写入文件

注：如果数值特征列中存在数值极大或极小的 outlier（通过 EDA 发现），应该使用更稳健（robust）的统计数据：用中位数而不是算术平均数，用分位数（quantile）而不是方差。这种标准化方法有一个重要的参数：（分位数下限，分位数上限），最好通过 EDA 的数据可视化确定。免疫 outlier。
归一化与标准化区别

(a) 目的不同，归一化是为了消除纲量压缩到[0,1]区间；标准化只是调整特征整体的分布。  (b) 归一化与最大，最小值有关；标准化与均值，标准差有关。 (c) 归一化输出在[0,1]之间；标准化无限制。
归一化与标准化应用场景
(a) 在分类、聚类算法中，需要使用距离来度量相似性的时候（如 SVM、KNN）或者使用 PCA 技术进行降维的时候，标准化(Z-score standardization)表现更好。  (b) 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将 RGB 图像转换为灰度图像后将其值限定在[0 255]的范围。  (c) 基于树的方法不需要进行特征的归一化。例如随机森林，bagging 与 boosting 等方法。如果是基于参数的模型或者基于距离的模型，因为需要对参数或者距离进行计算，都需要进行归一化。

3.5.2 非线性变换【统计变换】

利用统计或数学变换来减轻数据分布倾斜的影响。使原本密集的区间的值尽可能的分散，原本分散的区间的值尽量的聚合。
这些变换函数都属于幂变换函数簇，通常用来创建单调的数据变换。它们的主要作用在于它能帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。

1) log 变换

log 变换通常用来创建单调的数据变换。它的主要作用在于帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。因为 log 变换倾向于拉伸那些落在较低的幅度范围内自变量值的范围，倾向于压缩或减少更高幅度范围内的自变量值的范围。从而使得倾斜分布尽可能的接近正态分布。  所以针对一些数值连续特征的方差不稳定，特征值重尾分布我们需要采用 log 化来调整整个数据分布的方差，属于方差稳定型数据转换。
log 变换属于幂变换函数簇。该函数用数学表达式表示为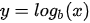  

自然对数使用 b=e，e=2.71828，通常叫作欧拉常数。你可以使用通常在十进制系统中使用的 b=10 作为底数。
代码实现

sns.distplot(df_titanic.fare,kde=False)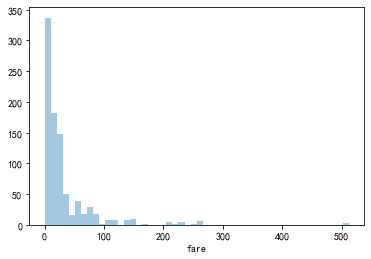

df_titanic['fare_log'] = np.log((1+df_titanic['fare']))
sns.distplot(df_titanic.fare_log,kde=False)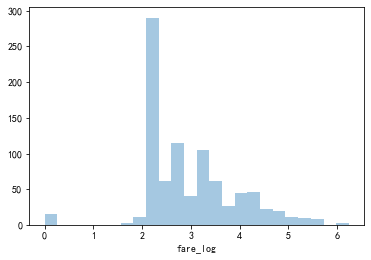

2)  box-cox 变换

box-cox 变换是另一个流行的幂变换函数簇中的一个函数。该函数有一个前提条件，即数值型值必须先变换为正数（与 log 变换所要求的一样）。万一出现数值是负的，使用一个常数对数值进行偏移是有帮助的。
box-cox 变换是 box 和 cox 在 1964 年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。box-cox 变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。box-cox 变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，box-cox 变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的。
box-cox 变换函数：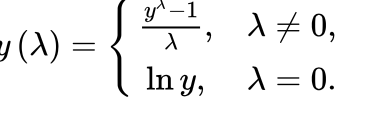

生成的变换后的输出 y 是输入 x 和变换参数的函数；当 λ=0 时，该变换就是自然对数 log 变换，前面我们已经提到过了。λ 的最佳取值通常由最大似然或最大对数似然确定。
代码实现

# 从数据分布中移除非零值
fare_positive_value = df_titanic[(~df_titanic['fare'].isnull()) & (df_titanic['fare']>0)]['fare']
import scipy.stats as spstats
# 计算最佳λ值
l, opt_lambda = spstats.boxcox(fare_positive_value)
print('Optimal lambda value:', opt_lambda) # -0.5239075895755266
# 进行 Box-Cox 变换
fare_boxcox_lambda_opt = spstats.boxcox(df_titanic[df_titanic['fare']>0]['fare'],lmbda=opt_lambda)
sns.distplot(fare_boxcox_lambda_opt,kde=Fal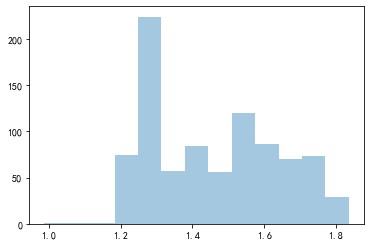

3.5.3 离散变量处理

1)  标签编码（label encoder）

LabelEncoder 是对不连续的数字或者文本进行编号，编码值介于 0 和 n_classes-1 之间的标签。
例如：比如有[dog,cat,dog,mouse,cat]，我们把其转换为[1,2,1,3,2]。这里就产生了一个奇怪的现象：dog 和 mouse 的平均值是 cat。
优点：相对于 OneHot 编码，LabelEncoder 编码占用内存空间小，并且支持文本特征编码。
缺点：它隐含了一个假设：不同的类别之间，存在一种顺序关系。在具体的代码实现里，LabelEncoder 会对定性特征列中的所有独特数据进行一次排序，从而得出从原始输入到整数的映射。所以目前还没有发现标签编码的广泛使用，一般在树模型中可以使用。
代码实现

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit(["超一线", "一线", "二线", "三线"])
print('特征：{}'.format(list(le.classes_)))
# 输出 特征：['一线', '三线', '二线', '超一线']
print('转换标签值：{}'.format(le.transform(["超一线", "一线", "二线"])))
# 输出 转换标签值：array([3 0 2]...)
print('特征标签值反转：{}'.format(list(le.inverse_transform([2, 2, 1]))))
# 输出 特征标签值反转：['二线', '二线', '三线

2) 独热编码（one hot encoder ）

OneHotEncoder 用于将表示分类的数据扩维。最简单的理解用 N 位状态寄存器编码 N 个状态，每个状态都有独立的寄存器位，且这些寄存器位中只有一位有效，只能有一个状态。
为什么要使用独热编码？
独热编码是因为大部分算法是基于向量空间中的度量来进行计算的，为了使非偏序关系的变量取值不具有偏序性，并且到圆点是等距的。使用 one-hot 编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用 one-hot 编码，会让特征之间的距离计算更加合理。  
为什么特征向量要映射到欧式空间？
将离散特征通过 one-hot 编码映射到欧式空间，是因为在回归、分类、聚类等机器学习算法中，特征之间距离或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算。
举个例子-假如有三种颜色特征：红、黄、蓝。
在利用机器学习的算法时一般需要进行向量化或者数字化。那么你可能想 假设 红=1，黄=2，蓝=3，那么这样实现了标签编码，即给不同类别以标签。然而这意味着机器可能会学习到“红<黄<蓝”，但这并不是我们的让机器学习的本意，只是想让机器区分它们，并无大小比较之意。
所以这时标签编码是不够的，需要进一步转换。因为有三种颜色状态，所以就有 3 个比特。即红色：1 0 0，黄色: 0 1 0，蓝色：0 0 1。如此一来每两个向量之间的距离都是根号 2，在向量空间距离都相等，所以这样不会出现偏序性，基本不会影响基于向量空间度量算法的效果。
优点：独热编码解决了分类器不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。它的值只有 0 和 1，不同的类型存储在垂直的空间。
缺点：只能对数值型变量二值化，无法直接对字符串型的类别变量编码。当类别的数量很多时，特征空间会变得非常大。在这种情况下，一般可以用 PCA 来减少维度。而且 one hot encoding+PCA 这种组合在实际中也非常有用。
代码实现

• 使用 pandas 实现:

sex_list = ['MALE', 'FEMALE', np.NaN, 'FEMALE', 'FEMALE', np.NaN, 'MALE']
df = pd.DataFrame({'SEX': sex_list})
display(df)
df.fillna('NA', inplace=True)
df = pd.get_dummies(df['SEX'],prefix='IS_SEX')
display(df)
# 原始数据
 SEX
0   MALE
1   FEMALE
2   NaN
3   FEMALE
4   FEMALE
5   NaN
6   MALE
# 填充后
 IS_SEX_FEMALE     IS_SEX_MALE    IS_SEX_NA
0    0                 1                0
1    1                 0                0
2    0                 0                1
3    1                 0                0
4    1                 0                0
5    0                 0                1 
pd.get_dummies(
 df_titanic,
 columns=[
 'sex', 'class', 'pclass', 'embarked', 'who', 'family_size', 'age_bin'
 ],drop_first=True)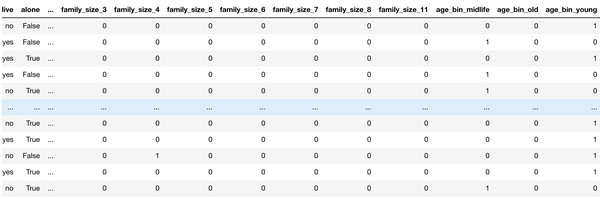

• 使用 sklearn 实现:

注：当特征是字符串类型时，需要先用 LabelEncoder() 转换成连续的数值型变量，再用 OneHotEncoder() 二值化 
sklearn.preprocessing 中的 OneHotEncoder 将 shape=(None,1)的列向量中每个分量表示的下标(index)编码成 one hot 行向量。
import numpy as np
from sklearn.preprocessing import OneHotEncoder
行向量转列向量：
# 非负整数表示的标签列表
labels = [0,1,0,2]
# 行向量转列向量
labels = np.array(labels).reshape(len(labels), -1)
one hot 编码：
enc = OneHotEncoder()
enc.fit(labels)
targets = enc.transform(labels).toarray()
# 如果不加 toarray() 的话，输出的是稀疏的存储格式，即索引加值的形式，也可以通过参数指定 sparse = False 来达到同样的效果
编码结果：
array([[ 1.,  0.,  0.],
 [ 0.,  1.,  0.],
 [ 1.,  0.,  0.],
 [ 0.,  0.,  1.]])

3)  标签二值化（LabelBinarizer）

 功能与 OneHotEncoder 一样，但是 OneHotEncoder 只能对数值型变量二值化，无法直接对字符串型的类别变量编码，而 LabelBinarizer 可以直接对字符型变量二值化。

3.5.4 降维

读取数据&数据展示

from sklearn import datasets
iris_data = datasets.load_iris()
X = iris_data.data
y = iris_data.target
def draw_result(X, y):
 """
 X:     降维后的数据
 iris:  原数据
 """
 plt.figure()
 # 提取 Iris-setosa
 setosa = X[y == 0]
 # 绘制点：参数 1 x 向量，y 向量
 plt.scatter(setosa[:, 0], setosa[:, 1], color="red", label="Iris-setosa")
 # Iris-versicolor
 versicolor = X[y == 1]
 plt.scatter(versicolor[:, 0], versicolor[:, 1], color="orange", label="Iris-versicolor")
 # Iris-virginica
 virginica = X[y == 2]
 plt.scatter(virginica[:, 0], virginica[:, 1], color="blue", label="Iris-virginica")
 plt.legend()
 plt.show()
draw_result(X, y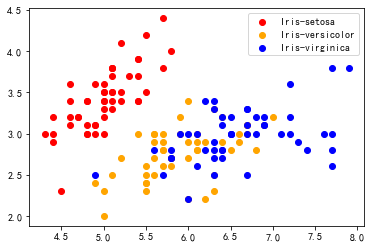

1) PCA（Principal Component Analysis）

作用：降维、压缩
步骤：

• 求 X 均值     
• 将 X 减去均值计算协方差矩阵 C = frac{1}{m}XX^T 
• 对协方差矩阵  C 特征值分解    
• 从大到小排列 C 的特征值取前 k 个特征值对应的特征向量按行组成矩阵即为变换矩阵 P_{ktimes n} 

(a) 手动实现 PCA

class PCA:
 def __init__(self, dimension, train_x):
 # 降维后的维度
 self.dimension = dimension
 # 原始数据集
 self.train_x = train_x
 @property
 def result(self):
 '返回降维后的矩阵'
 # 1. 数据中心化
 data_centering = self.train_x - np.mean(self.train_x, axis=0)
 # 2. 计算协方差矩阵
 cov_matrix = np.cov(data_centering, rowvar=False)
 # 3. 特征值分解
 eigen_val, eigen_vec = np.linalg.eig(cov_matrix)
 # 4. 生成降维后的数据
 p = eigen_vec[:, 0:self.dimension]  # 取特征向量矩阵的前 k 维
 return np.dot(data_centering,p) 
调用方法：
pca = PCA(2,X)
iris_2d = pca.result
draw_result(iris_2d, y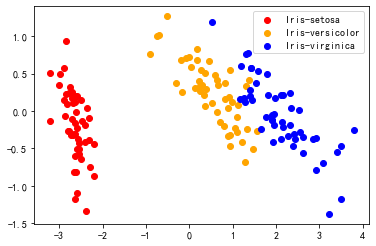

(b) sklearn 的 PCA

import numpy as np
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newX = pca.fit_transform(X)
draw_result(newX, y)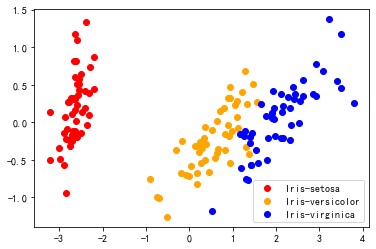

2) SVD（Singular Value Decomposition）

作用：特征分解、降维
步骤：

(a)手动实现 SVD

class SVD:
 def __init__(self, dimension, train_x):
 self.dimension = dimension
 self.train_x = train_x
 @property
 def result(self):
 '返回降维后的矩阵'
 data_centering = self.train_x - np.mean(self.train_x, axis=0)
 # SVD
 U, Sigma, VT = np.linalg.svd(data_centering)
 return np.dot(data_centering, np.transpose(VT)[:, :self.dimension])
调用方法：
svd = SVD(2,X)
iris_svd = svd.result
draw_result(iris_svd,y)

(b) sklearn 的 SVD
TruncatedSVD，截断奇异值分解（当数据量非常大，svd 跑不出来时使用此方法）。

from sklearn.decomposition import TruncatedSVD
iris_2d = TruncatedSVD(2).fit_transform(X)
draw_result(iris_2d, y)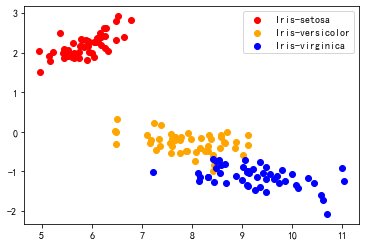

3)  PCA 和 SVD 的关系

4)  Fisher 线性判别分析（Linear Discriminant Analysis,LDA）

是有监督的降维，通过最小化类内离散度与最大化类间离散度来获得最优特征子集。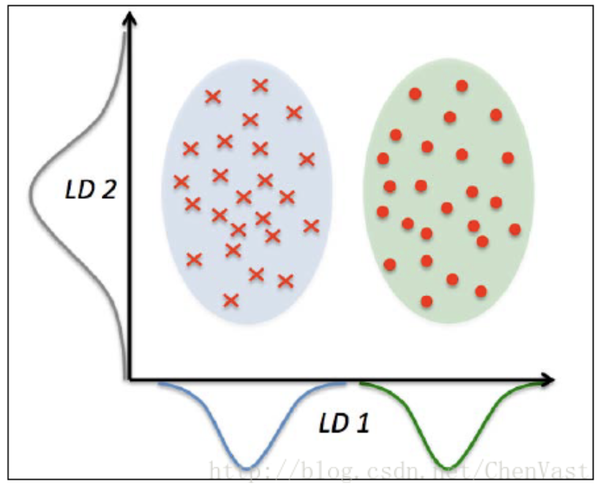 

LD1 通过线性判定，可以很好的将呈正态分布的两个类分开。 LD2 的线性判定保持了数据集的较大方差，但 LD2 无法提供关于类别的信息，因此 LD2 不是一个好的线性判定。

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
iris_2d = lda.fit_transform(X, y)
draw_result(iris_2d, y)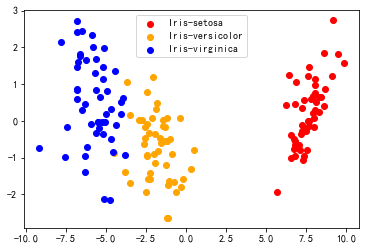

LDA 与 PCA 相似：

PCA 试图寻找到方差最大的正交的主成分分量轴 LDA 发现可以最优化分类的特征子空间 LDA 和 PCA 都是可用于降低数据集维度的线性转换技巧 PCA 是无监督算法 LDA 是监督算法 LDA 是一种更优越的用于分类的特征提取技术

5) T-SNE

from sklearn.manifold import TSNE
tsne = TSNE(n_components=2)
iris_2d = tsne.fit_transform(X)
draw_result(iris_2d, y)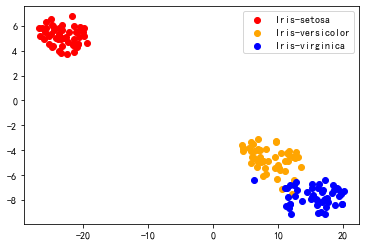

五 总结

切忌：一开始就把所有的特征一股脑地扔进模型，容易被一些没用的特征误导。
1) EDA
plot，plot，plot，重要的事情说三遍
2) 特征预处理
时间序列：把昨天的特征加入今天的特征，或者把和昨天相比，特征数值的改变量加入今天的特征。
连续特征离散化（决策树类型的模型没意义）:一种挺有趣的变种，就是限制浮点数特征的精度，异常数据有很强的鲁棒性，模型也会更稳定。
clipping：可以用 pandas dataframe 的.clip(low, upper)方法，把特征值的取值限制在一定范围内
3) 数据清洗
要合情合理，不可盲目填充缺失值、删除异常值，要建立在统计科学基础上。
4) 特征变换
除非万不得已，不要用 PCA 或者 LDA 降维，建议直接减原始特征。

• 特征变换要切记：

任何针对单独特征列的单调变换（如对数）：不适用于决策树类算法。
对于决策树而言，   X、X^3、X^5  之间没有差异 ， |X|、X^2、X^4 之间没有差异，除非发生了舍入误差。
线性组合（linear combination）：仅适用于决策树以及基于决策树的 ensemble（如 gradient boosting, random forest），因为常见的 axis-aligned split function 不擅长捕获不同特征之间的相关性；不适用于 SVM、线性回归、神经网络等。

• 类别特征与数值特征的组合：

用 N1 和 N2 表示数值特征，用 C1 和 C2 表示类别特征，利用 pandas 的 groupby 操作，可以创造出以下几种有意义的新特征：（其中，C2 还可以是离散化了的 N1）

median(N1)_by(C1)   中位数
mean(N1)_by(C1)   算术平均数
mode(N1)_by(C1)   众数
min(N1)_by(C1)   最小值
max(N1)_by(C1)   最大值
std(N1)_by(C1)   标准差
var(N1)_by(C1)   方差
freq(C2)_by(C1)   频数

仅仅将已有的类别和数值特征进行以上的有效组合，就能够大量增加优秀的可用特征。
将这种方法和线性组合等基础特征工程方法结合（仅用于决策树），可以得到更多有意义的特征，如：

N1 - median(N1)_by(C1)
N1 - mean(N1)_by(C1)

• 用基因编程创造新特征

基于 genetic programming 的 symbolic regression【python 环境下首推基因编程库为 gplearn】。
基因编程的两大用法：
转换（transformation）：把已有的特征进行组合转换，组合的方式（一元、二元、多元算子）可以由用户自行定义，也可以使用库中自带的函数（如加减乘除、min、max、三角函数、指数、对数）。组合的目的，是创造出和目标 y 值最“相关”的新特征。
spearman 多用于决策树（免疫单特征单调变换），pearson 多用于线性回归等其他算法。
回归（regression）：原理同上，只不过直接用于回归而已。

• 用决策树创造新特征：

在决策树系列的算法中（单棵决策树、gbdt、随机森林），每一个样本都会被映射到决策树的一片叶子上。因此，我们可以把样本经过每一棵决策树映射后的 index（自然数）或 one-hot-vector（哑编码得到的稀疏矢量）作为一项新的特征，加入到模型中。
具体实现：apply()以及 decision_path()方法，在 scikit-learn 和 xgboost 里都可以用。
5) 模型

• 树模型：

对特征数值幅度不敏感，可以不进行无量纲化和统计变换处理； 由于数模型依赖于样本距离来进行学习，可以不进行类别特征编码（但字符型特征不能直接作为输入，所以需要至少要进行标签编码）。 LightGBM 和 XGBoost 都能将 NaN 作为数据的一部分进行学习，所以不需要处理缺失值。其他情况下，我们需要使用。

• 依赖样本距离来学习的模型（如线性回归、SVM、深度学习等）：

对于数值型特征需要进行无量纲化处理； 对于一些长尾分布的数据特征，可以做统计变换，使得模型能更好优化； 对于线性模型，特征分箱可以提升模型表达能力；
注：结合工作内容、学习总结以上内容，如有错误，请指出，诚心请教

参考资料

光喻：【持续更新】机器学习特征工程实用技巧大全zhuanlan.zhihu.com
特征工程系列：数据清洗 - 大咖驾到 - 博客园www.cnblogs.com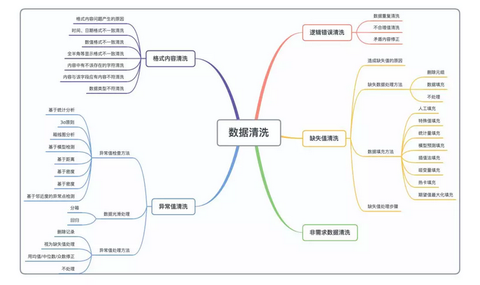

作者：王岳 好未来机器学习算法专家