数据集
首先数据集选择使用Cifar-10。
这个数据集合包含十个类的图片,每类6000张32 x 32的图片,共计60000张图片,其中50000训练图片,10000张测试图片。
这里下载了python对应的版本:
读取文件
在Cifar-10的网站,我们可以找到实例代码,然后按照自己的文件目录读取:
CIRFA_DIR = "../data/cifar-10-batches-py"
def load_data(filename):
# 从文件中读取数据
with open(filename, 'rb') as f:
# pickle 默认是用ASCII编码,但是待载入文件并不是使用ASCII编码的,需要声明encoding, 来正确载入文件
data = cPickle.load(f, encoding='latin1')
return data['data'], data['labels']这里与实例代码有点不同,在load()函数中,添加了一个encoding参数,因为默认载入文件是使用ASCII编码,但是数据集文件并不是使用这个编码的,所以要正确打开,需要添加encoding='latin1',否则不能正确解码文件。
数据处理——加载Cifar样本
这里创建一个CifarData类,用来加载样本文件中的数据:
class CifarData:
def __init__(self, filenames, need_shuffle):
all_data = []
all_labels = []
for filename in filenames:
data, labels = load_data(filename)
all_data.append(data)
all_labels.append(labels)
self._data = np.vstack(all_data) # 将data纵向合并为一个矩阵
self._data = self._data / 127.5 - 1 # 将data作一个归一化,0到1之间
self._labels = np.hstack(all_labels) # 将labels横向合并为一个矩阵
self._num_examples = self._data.shape[0] # 样本数
self._need_shuffle = need_shuffle # 保留need_shuffle
self._indicator = 0 # 指明在当前数据集,把这个数据集遍历到哪个位置上
if self._need_shuffle:
self._shuffle_data()注意到这里在init函数中,定义了一个need_shuffle的变量。
对于训练集来说,需要在训练一遍之后进行数据的打乱,也就是shuffle,以防顺序数据产生的过拟合问题;
对于测试集来说,不在测试集上进行训练,只计算损失函数和准确率,也就不需要进行shuffle。
然后在这个类里,还需要定义两个函数:
# 重新打乱数据
def _shuffle_data(self):
# 对_num_example这些数据进行混排
p = np.random.permutation(self._num_examples)
self._data = self._data[p]
self._labels = self._labels[p]首先是shuffle函数,来对训练集数据进行打乱。
# 每次返回batch_size个样本
def next_batch(self, batch_size):
end_indicator = self._indicator + batch_size # 定义每个batch的结束位置
# 如果结束位置大于全部的数组
if end_indicator > self._num_examples:
# 如果可以shuffle,
if self._need_shuffle:
self._shuffle_data()
self._indicator = 0
end_indicator = batch_size
# 数据集已经遍历完,并且不允许进行shuffle
else:
raise Exception("have no more examples")
# 验证batch_size是否比整个样本数还要大
if end_indicator > self._num_examples:
raise Exception("batch size is larger than all examples")
# 返回indicator 到 end_indicator 之间的数据
batch_data = self._data[self._indicator: end_indicator]
batch_labels = self._labels[self._indicator: end_indicator]
self._indicator = end_indicator # 重新定位indicator
return batch_data, batch_labels然后定义了next_batch()函数,用来每次返回batch_size大小的数据。并在每次返回后,对剩余数据进行打乱。
初始化相关变量
# 这里占位符的第一维度为None,表示样本数是不确定的;第二维度为3072,表示每个样本的维度是3072
x = tf.placeholder(tf.float32, [None, 3072])
y = tf.placeholder(tf.int64, [None])
# 定义权重,并在均值为0,方差为1的范围内进行随机初始化 (3072 * 10)# 进行多分类,样本数据总共有十个类
w = tf.get_variable('w', [x.get_shape()[-1], 10],
initializer=tf.random_normal_initializer(0, 1))
# 定义偏置,初始化为常量0 (10, )
b = tf.get_variable('b', [10], initializer=tf.constant_initializer(0.0))
# (None, 3072) * (3072, 10) = (None, 10)
y_ = tf.matmul(x, w) + b在神经网络中,神经元的基本结构如下,x1、x2、x3...是输入,h(W*x)是输出,W*x是一个中间过程,表示让每个x和其权重做乘积,然后再加起来,再由h函数得到输出。这里只有一个输出,就表示是单神经元:
这里面的w、x就对应代码中定义的w和x,然后输出就是y。这里还有一个偏置b,这就是我们之前数学中所学到截距的概念类似,也就是分类线或分类面与坐标轴交点的值:
然后y_是一个W和x进行矩阵相乘,它是一个内积值。后面需要将其变成一个概率值。
然后使用激活函数(即公式中的f)对y_进行激活:
# 多分类的激活函数: e^x / sum(e^x)
# [[0.01, 0.9, ..., 0.03], [...]]
p_y = tf.nn.softmax(y_)这是多分类的激活函数softmax(),而二分类的激活函数一般使用sigmoid()函数。
接着对y进行one_hot编码,这步主要是为了将y和p_y转换成相同的数据格式:
# 对y进行 ont_hot 编码,使得y和p_y保持相同的数据类型,以计算损失函数
# 5 -> [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
y_one_hot = tf.one_hot(y, 10, dtype=tf.float32)最后计算损失函数:
# 计算损失函数
loss = tf.reduce_mean(tf.square(y_one_hot - p_y))这里计算损失函数,采用了平方差的方式。
最后对准确率进行计算,并对loss做梯度下降(梯度下降算法),找到loss的最小值:
predict = tf.argmax(y_, 1) # 预测值
correct_predict = tf.equal(predict, y) # 正确的预测值
accuracy = tf.reduce_mean(tf.cast(correct_predict, tf.float64)) # 准确率
# 对loss做梯度下降
with tf.name_scope('train_op'):
train_op = tf.train.AdamOptimizer(1e-3).minimize(loss)进行训练
首先先执行初始化的变量,然后定义训练的batch_size、训练的步数、测试的步数。
# 执行初始化
init = tf.global_variables_initializer()
batch_size = 20
train_steps = 100000
test_steps = 100接着使用session开始执行计算:
with tf.Session() as sess:
sess.run(init)
# 循环train_steps,进行训练
for i in range(train_steps):
batch_data, batch_labels = train_data.next_batch(batch_size)
loss_val, accu_val, _ = sess.run(
[loss, accuracy, train_op],
feed_dict={
x: batch_data,
y: batch_labels})
# 打印中间过程
if (i + 1) % 500 == 0:
print('[Train] step: %d, loss: %4.5f, acc: %4.5f' % (i + 1, loss_val, accu_val))
# 使用测试集进行评测
if (i + 1) % 5000 == 0:
test_data = CifarData(test_filename, False)
all_test_acc_val = [] # 保存总的accuracy
for j in range(test_steps):
test_batch_data, test_batch_labels = test_data.next_batch(batch_size)
test_acc_val = sess.run([accuracy], feed_dict={x: test_batch_data, y: test_batch_labels})
all_test_acc_val.append(test_acc_val)
test_acc = np.mean(all_test_acc_val) # 对test的acc做平均
print('[Test] step: %d, acc: %4.5f' % (i + 1, test_acc))tensorflow只有让计算图上的节点在session中执行才能得到结果,sess只有在调用run()函数后才能开始执行计算。而一般调用run()函数后,执行计算会十分消耗资源,所以必须要在结束后执行close()进行关闭:
sess.run(init)
sess.close()但是手动进行关闭又比较麻烦,有时候还会忘记,所以就是用with语句,结束后自动关闭:
with tf.Session as sess:
sess.run(init)初始化执行后,开始循环train_steps,进行训练。
在每执行500步打印一次中间过程,输出当前步、损失函数和准确率。
同时,为了做出类似真是环境中的评测,需要在测试集上记性评测。每5000步对已训练的模型进行一次评测。
运行结果及总结
我们发现随着训练的进行,准确率在整体上有一定程度的提升。
通过对单个神经元的神经网络到多个神经元的神经网路的学习,对实现神经网络的基本过程有了一定程度的了解。
对于数据处理部分,归一化处理对结果的影响十分重要:
self._data = self._data / 127.5 - 1没有进行归一化之前,训练的准确率基本没有什么变化,这是因为未归一化的数据都比较大,这就导致了运算会偏向某一方,从而导致准确率的变化不大。
其次,在处理数据的时候,还要多注意数据类型的关系。因为其中很多都是矩阵的乘法,一旦数据类型或格式不能匹配,就不能正确运算。
对于神经网络的处理部分,主要就是理解特征集(x)、损失函数(loss)等概念。通过编程的实现,对文章开始部分的方程的理解不仅仅限制在数学层面:
包括推梯度下降的应用,对激活函数的应用等。
相关参考:
https://tensorflow.google.cn/versions/r2.0/api_docs/python/tf
https://www.imooc.com/learn/1063




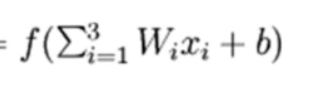

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。