最大异或和

一、字典树

用来高效的存储查找字符串集合 也可以存储二进制信息

1. 存储

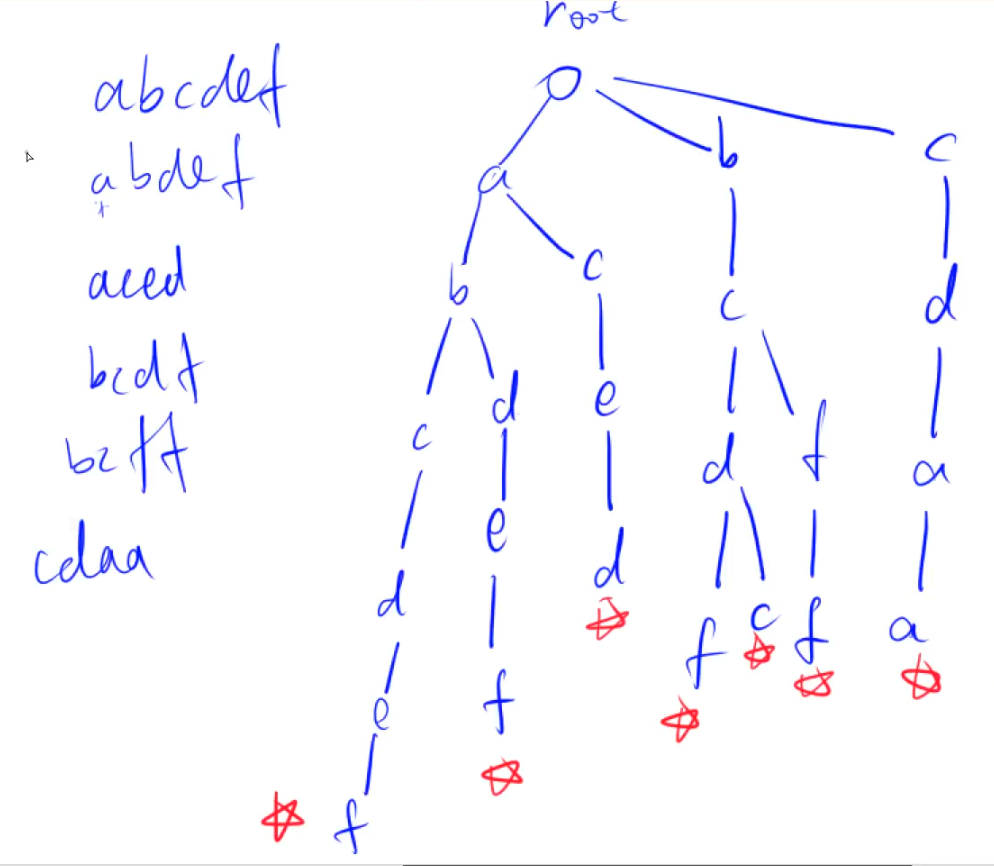
字典树存储形式如下：其中每个单词的末尾会做上一个 标记

---

2. 查找

   • 判断单词是否在路径上
   • 如果在路径上，判断单词末尾是否存在标记

完整代码如下：

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点, 26是假设仅有小写字母, 则每个节点的孩子最多为26个
// cnt[]存储以每个节点结尾的单词数量
// idx 表示每个节点的索引

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx; // 如果没有这个字符作为子节点，则新建
        p = son[p][u]; // 如果存在则以找到的这个节点为父节点向下寻找
    }
    cnt[p] ++ ; // 单词数加一
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

二、字典树相关题目

143. 最大异或对

1. 异或和性质

异或被称为无进位加法，所以其与加法性质类似。

假设数 x 的二进制表示为 $x_n...x_1x_0$，数 y 的二进制表示为 $y_n...y_0$则二者的异或和为各位的异或结果乘以当前位的权值。即 $(x_n \bigoplus y_n) \times 2^n + ... + (x_0 \bigoplus y_0) \times 2^0$

2. 解体思路

由上述性质可知为找到与 x 异或和最大的数，应优先找到与其高位二进制位相反的值，这里可以利用 trie树 来存储每个数字的二进制位。 存储时应由高位往低位，优先找高位与此位不同的数。
样例字典树形式为：

完整代码：

#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5, M = N * 31; // 字典树的深度最高为 N * 31

int son[M][2], idx; // 定义字典树

int n, q[N];

// 将一个数加入字典树中
void insert(int x) {
    int p = 0;
    for (int i = 30; i >= 0; i--) { // 从最高位开始遍历
        int u = x >> i & 1; // 拿到x的第i位
        if (!son[p][u]) son[p][u] = ++ idx; // 如果父节点没有这个孩子则插入
        p = son[p][u]; // 更换父节点
    }
}

// 查找与x异或和最大的一棵树
int query(int x) {
    int p = 0;
    int res = 0;
    for (int i = 30; i >= 0; i--) {
        int u = (x >> i) & 1;
        if (son[p][!u]) { p = son[p][!u], res += 1 << i; } // 查找有没有与当前位相反的数存在
        else p = son[p][u];
    }
    return res;
}

int main() {
    int res = 0;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
        insert(q[i]); 
        res = max(query(q[i]), res);
    };
    printf("%d", res);
    return 0;
}

---

3485. 最大异或和 - AcWing题库

算法要点： 将一段数的异或和最大值，转换为两个值的异或和最大值。
思路： 由于异或和具有类似加法的性质，所以可以采用类似前缀和的思路。

$$ 设：S_n = a_1 \bigoplus a_2 ... \bigoplus a_n \\ 则有：S_{i-1} \bigoplus S_{i...j} = S_j \\ 所以： S_{i...j} = S_j \bigoplus S_{i-1} $$

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, M = N * 31; // 字典树的深度最高为 N * 31

int son[M][2], idx, cnt[M]; // 定义字典树

int n, m, s[N];

// 将一个数加入字典树中
void insert(int x, int v) {
    int p = 0;
    for (int i = 30; i >= 0; i--) { // 从最高位开始遍历
        int u = x >> i & 1; // 拿到x的第i位
        if (!son[p][u]) son[p][u] = ++ idx; // 如果父节点没有这个孩子则插入
        p = son[p][u]; // 更换父节点
        cnt[p] += v;
    }
}

// 查找与x异或和最大的一棵树
int query(int x) {
    int p = 0;
    int res = 0;
    for (int i = 30; i >= 0; i--) {
        int u            = (x >> i) & 1;
        if (cnt[son[p][!u]]) { p = son[p][!u], res += 1 << i; } // 查找有没有与当前位相反的数存在
        else p = son[p][u];
    }
    return res;
}

int main() {
    int res = 0;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &s[i]);
        s[i] = s[i] ^ s[i - 1];
    };

    insert(s[0], 1);

    for (int i = 1; i <= n; i++) {
        if (i > m) insert(s[i - m - 1], -1); // 当i大于m时删掉距离当前大于m的数
        res = max(res, query(s[i]));
        insert(s[i], 1);
    } 

    printf("%d\n", res);
    return 0;
}