Why does floating-point number arithmetic produce errors

Preface

Everyone will encounter so-called floating-point errors when writing code. If you have not stepped on the pit of floating-point errors, you can only say that you are too lucky.

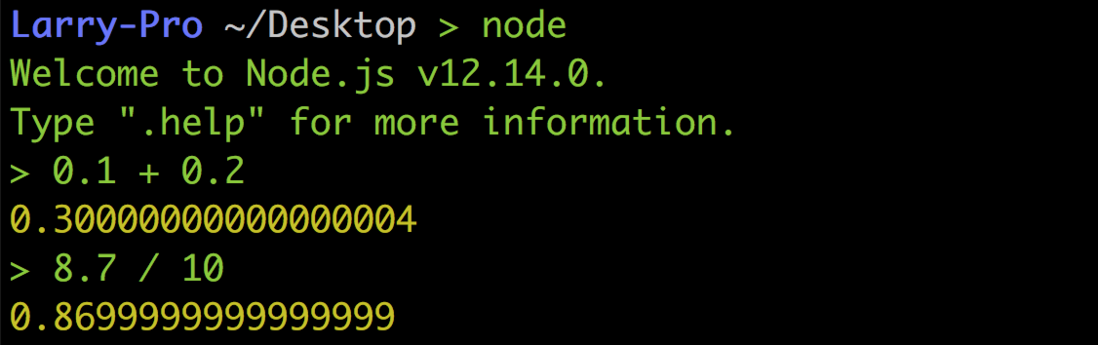
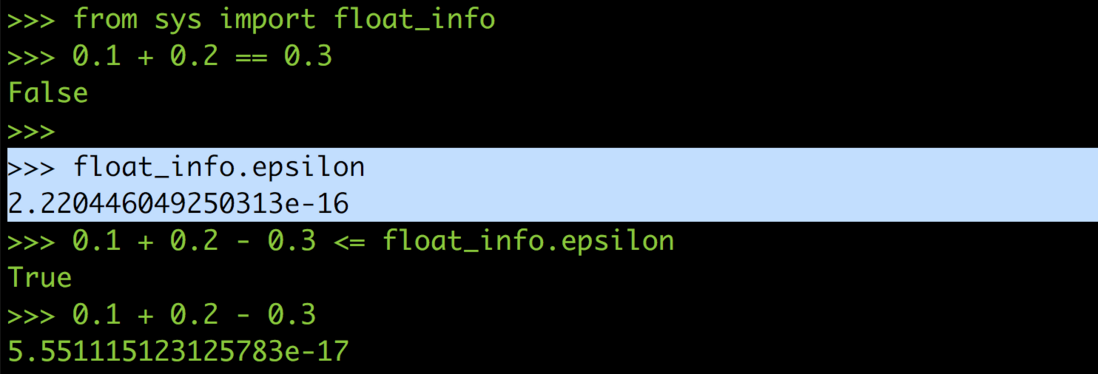
Take the Python in the following figure as an example, 0.1 + 0.2 is not equal to 0.3 , 8.7 / 10 is not equal to 0.87 , but 0.869999… , which is really strange 🤔

But this is definitely not a bug in the underworld, nor is it that Python is designed to be a problem, but the inevitable result of floating-point numbers when doing calculations, so it is the same even in JavaScript or other languages:

How does the computer store an integer (Integer)

Before talking about why there are floating-point errors, let’s talk about how computers use 0 and 1 to represent a integer . Everyone should know binary: for example, 101 represents $2^2 + 2^0$, which is 5. 1010 represents $2^3 + 2^1$ which is 10.

If it is an unsigned 32-bit integer, it means that it has 32 positions where 0 or 1 can be placed, so the minimum value is 0000...0000 which is 0, and the maximum value 1111...1111 represents $2^{31} + 2^{30} + .. . + 2^1 + 2^0$ which is 4294967295

From the perspective of permutation and combination, because each bit can be 0 or 1, the value of the entire variable has $2^{32}$ possibilities, so can be exactly express 0 to $2^{23}- Any value between 1$ will not have any error.

Floating Point

Although there are many integers from 0 to $2^{23}-1$, the number is ultimately limited to , which is just as many as $2^{32}$; but floating-point numbers are different, we can Think of it this way: There are only ten integers in the range from 1 to 10, but there are infinitely many floating-point numbers, such as 5.1, 5.11, 5.111, etc., and the list is endless.

But because there are only 2³² possibilities in the 32-bit space, in order to pack all floating-point numbers in this 32-bit space, many CPU manufacturers have invented various floating-point number representation methods, but if the format of each CPU not the same too much, so in the end is the IEEE released the IEEE 754 as a common standard floating-point operations, and now also follow this standard CPU design.

IEEE 754

There are many things defined in IEEE 754, including single precision (32 bit), double precision (64 bit), and the representation of special values (infinity, NaN), etc.

Normalization

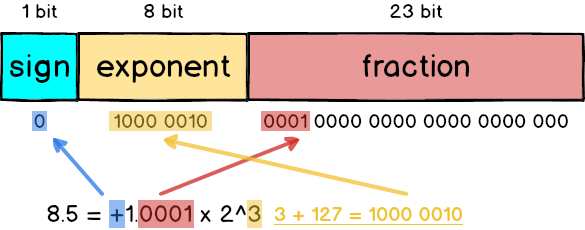
For the floating-point number of 8.5, if you want to change it into IEEE 754 format, you must first do some normalization: split 8.5 into 8 + 0.5, which is $2^3 + (\cfrac{1}{2})^1$ , Then write it in binary to become 1000.1 , and finally write it as $1.0001 \times 2^3$, which is very similar to decimal scientific notation.

Single-precision floating-point number

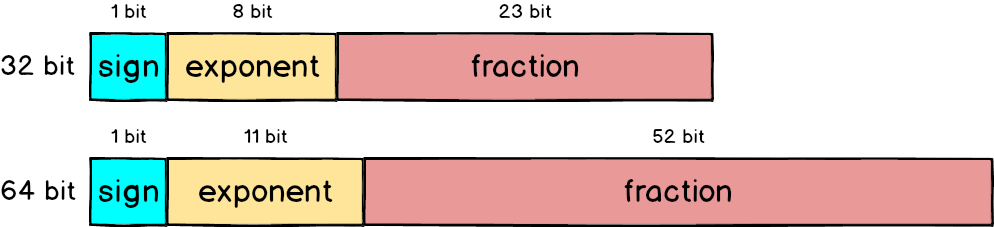
In IEEE 754, the 32-bit floating-point number is divided into three parts, namely the sign, exponent and fraction, which add up to 32 bits.

• Sign: The leftmost 1 bit represents the sign. If the number is positive, sign will be 0, otherwise it will be 1.
• : The 8 bit in the middle represents the normalized power number, and it uses the format of 160ef7a8aaee29 order code true value +127 , that is, 3 plus 127 equals 130
• Fraction: The 23 bit on the far right is the decimal part. For 1.0001 , it is 1. after 0001

So if 8.5 is expressed as 32 bit format, it should be like this:

Under what circumstances will errors occur?

The previous example of 8.5 can be expressed as $2^3 + (\cfrac{1}{2})^1$ because 8 and 0.5 are both powers of 2, so there will be no accuracy problems at all .

But if it is 8.9, because there is no way to add it to the power of 2, it will be forced to express as $1.0001110011... \times 2^3$, and an error of about $0.0000003$ will be generated. If you are curious about the result, you can to 160ef7a8aaef12 IEEE-754 Floating Point Converter website to play.

Double-precision floating-point number

The single-precision floating-point number mentioned above only uses 32 bits to represent. In order to make the error smaller, IEEE 754 also defines how to use 64-bit to represent floating-point numbers. Compared with 32 bits, the fraction part is more than twice as large. 23 bit becomes 52 bit, so the accuracy will naturally increase a lot.

Take 8.9 as an example. Although it can be more accurate with 64-bit representation, because 8.9 cannot be completely written as a sum of powers of 2, there will still be errors in 16 digits below the decimal, but the error with single precision is 0.0000003 Is much smaller than that

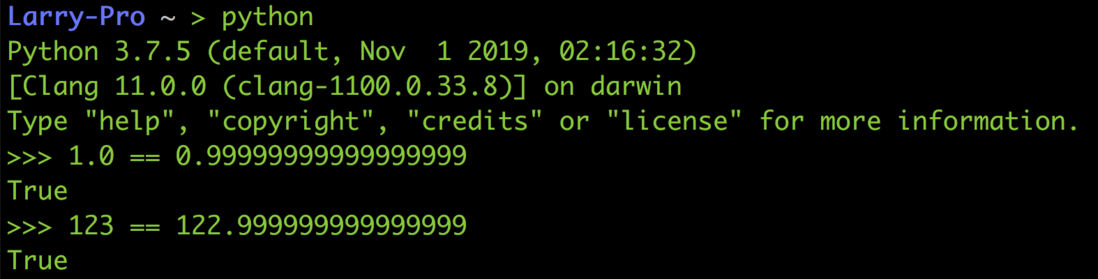
A similar situation also like Python in 1.0 with 0.999...999 are equal, 123 with 122.999...999 also equal, because the gap between them has been too small to be placed fraction inside, so it seems from the binary format they are every bit it's the same.

Solution

Since the error of floating-point numbers is unavoidable, you have to live with it. Here are two more common ways to deal with it:

Set the maximum allowable error ε (epsilon)

In some languages, the so-called epsilon is provided to let you judge whether it is within the allowable range of floating-point error. In Python, the value of epsilon is approximately $2.2e^{-16}$

So you can rewrite 0.1 + 0.2 == 0.3 0.1 + 0.2 — 0.3 <= epsilon during the calculation process, and correctly compare 0.1 plus 0.2 to see if it is equal to 0.3.

Of course, if the system does not provide it, you can also define an epsilon by yourself, set it to about 2-15 power

Fully use decimal for calculations

The reason for the floating point error is that in the process of converting decimal to binary, there is no way to put all the decimal parts into the mantissa. Since the conversion may have errors, then simply don’t convert it and use decimal. Do calculations.

There is a module in Python called decimal , and there is a similar package in JavaScript. It can help you calculate with decimal system, just like if you use pen and paper to calculate 0.1 + 0.2, there will be absolutely no error or any error.

Although calculations in decimal can completely avoid floating-point errors, because Decimal's decimal calculations are simulated, binary calculations are still used in the lowest-level CPU circuit, and the execution will be much slower than native floating-point calculations. Therefore, it is not recommended to use Decimal for all floating-point operations.