一.相似度计算方法
- 欧式距离
- 杰卡德(Jaccard)相似度
- 余弦相似度
- 皮尔逊(Pearson)相似度
1.欧式距离
欧式空间下度量距离的方法,两个物体, 都在同一个空间下表示为两个点, 假如叫做p,q, 分别都是n个坐标, 那么欧式距离就是衡量这两个点之间的距离. 欧氏距离不适用于布尔向量之间
计算公式:
$$ xE(p,q) = \sqrt{\sum_{i=1}^n (p_i - q_i)^2} $$
欧氏距离的值是一个非负数, 最大值正无穷, 通常计算相似度的结果希望是[-1,1]或[0,1]之间,一般可以使用
如下转化公式:
$$ 1/1+E(p,q) $$
2.杰卡德(Jaccard)
两个集合的交集元素个数在并集中所占的比例, 非常适用于布尔向量表示,分子是两个布尔向量做点积计算, 得到的就是交集元素的个数,母是两个布尔向量做或运算
计算公式:
代码实现:
def jaccard_similar():
Nu = {'A', 'C', 'D'}
Nv = {'A', 'B', 'D', 'E'}
similarity = len(Nu & Nv) / len(Nu | Nv)
print(similarity)3.余弦相似度
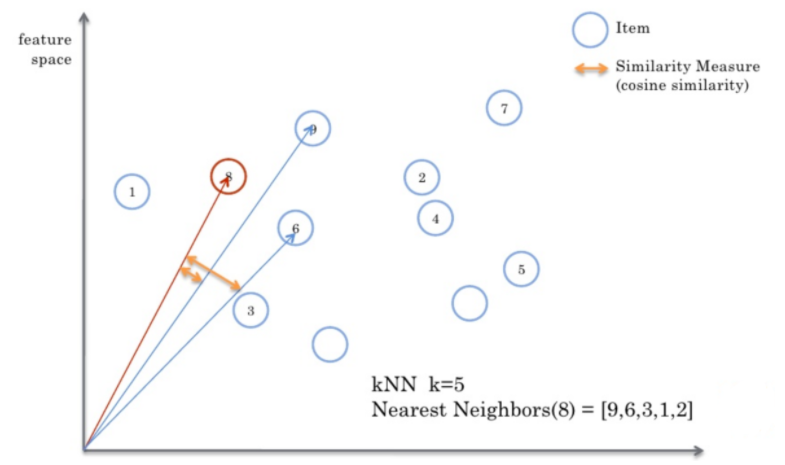
度量的是两个向量之间的夹角, 用夹角的余弦值来度量相似的情况,余弦相似度在度量文本相似度, 用户相似度,物品相似度的时候较为常用余弦相似度的特点, 与向量长度无关,余弦相似度计算要对向量长度归一化, 两个向量只要方向一致,无论程度强弱, 都可以视为'相似'
计算公式:
代码实现:
def UserSimilarity(train):
W = dict()
for u in train.keys():
for v in train.keys():
if u == v:
continue
W[u][v] = len(train[u] & train[v])
W[u][v] /= math.sqrt(len(train[u]) * len(train[v]) * 1.0)
return W 4.皮尔逊(Pearson)相似度
实际上也是一种余弦相似度, 不过先对向量做了中心化, 向量a b 各自减去向量的均值后, 再计算余弦相似度,皮尔逊相关系数度量的是两个变量的变化趋势是否一致, 不适合计算布尔值向量之间的相关度
计算公式:
代码实现:
调用pandas.DataFrame中的corr()方法
ratings_matrix.T.corr()

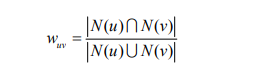


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。