Tree data structure in JavaScript

Tree data structure in JavaScript

Implementation and traversal technology

Author: Anish Kumar Translator: Classmate Xiaoqiang Source: stackfull

Tree is an interesting data structure, it has a wide range of applications in various fields, such as:

• DOM is a tree data structure
• The directories and files in our operating system can be represented as trees
• The family hierarchy can be represented as a tree

There are many variants of the tree (such as heap, BST, etc.) that can be used to solve problems related to scheduling, image processing, and databases. Many complex problems may seem to have nothing to do with the tree, but they can actually be expressed as a problem. We will also discuss these issues (in later parts of this series) and see how trees can make seemingly complex problems easier to understand and solve.

introduction

It is very simple to node for a binary tree.

function Node(value){
  this.value = value
  this.left = null
  this.right = null
}
// usage
const root = new Node(2)
root.left = new Node(1)
root.right = new Node(3)

Therefore, these few lines of code will create a binary tree for us, which looks like this:

           2  
        /      \
       /         \
     1            3
   /   \        /    \
null  null   null   null

this is very simple. Now, how do we use this?

Traverse

Let's start by trying to traverse these connected tree nodes (or the entire tree). Just like we can iterate over an array, it would be better if we could also "iterate" the tree nodes. However, trees are not linear data structures like arrays, so there is more than one way to traverse these data structures. We can roughly divide traversal methods into the following categories:

• Breadth first traversal
• Depth first traversal

Breadth First Search/Traversal (BFS)

In this method, we traverse the tree layer by layer. We will start from the root, then cover all the children, and cover all the second-level children, and so on. For example, for the tree above, the traversal will get the following results:

2, 1, 3

Here is an example of a slightly more complicated tree to make this easier to understand:

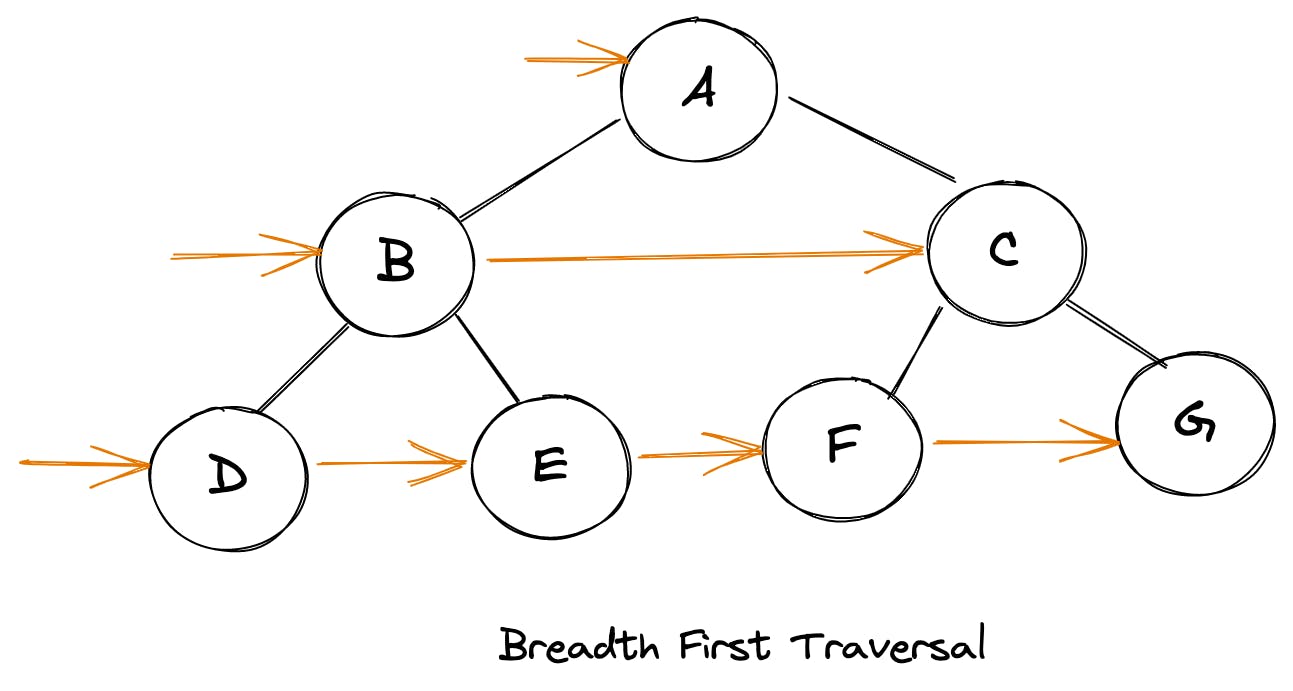
To achieve this form of traversal, we can use a queue (first in first out) data structure. Here is what the entire algorithm looks like:

• Initialize a queue containing root
• Remove the first item from the queue
• Push the left and right children of the pop-up item into the queue
• Repeat steps 2 and 3 until the queue is empty

Here is what this algorithm looks like after its implementation:

function walkBFS(root){
  if(root === null) return

  const queue = [root]
  while(queue.length){
      const item = queue.shift()
      // do something
      console.log(item)

      if(item.left) queue.push(item.left)
      if(item.right) queue.push(item.right)
   }
}

We can slightly modify the above algorithm to return a two-dimensional array, where each internal array represents a level containing elements:

function walkBFS(root){
  if(root === null) return

  const queue = [root], ans = []

  while(queue.length){
      const len = queue.length, level = []
      for(let i = 0; i < len; i++){
          const item = queue.shift()
          level.push(item)
          if(item.left) queue.push(item.left)
          if(item.right) queue.push(item.right)
       }
       ans.push(level)
   }
  return ans
}

Depth First Search/Traversal (DFS)

In DFS, we take a node and continue to explore its children until the depth is completely exhausted. This can be achieved by one of the following methods:

 root node -> left node -> right node // pre-order traversal
 left node -> root node -> right node // in-order traversal
 left node -> right node -> root node // post-order traversal

All of these traversal techniques can be implemented iteratively and recursively, let's get into the implementation details:

Preorder traversal

The following is what the preorder traversal of a tree looks like:

 root node -> left node -> right node

The trick:
We can use this simple trick to manually find the preorder traversal of any tree: traverse the entire tree from the root node, keeping ourselves on the left.

accomplish:
Let us delve into the actual implementation of this traversal. recursive method is quite intuitive.

function walkPreOrder(root){
  if(root === null) return

  // do something here
  console.log(root.val)

  // recurse through child nodes
  if(root.left) walkPreOrder(root.left)
  if(root.right) walkPreOrder(root.right)
}

iteration method of preorder traversal is very similar to BFS, except that we use the stack instead of the queue, and we first put the right child element on the stack:

function walkPreOrder(root){
  if(root === null) return

  const stack = [root]
  while(stack.length){
      const item = stack.pop()

      // do something
      console.log(item)

      // Left child is pushed after right one, since we want to print left child first hence it must be above right child in the stack
      if(item.right) stack.push(item.right)
      if(item.left) stack.push(item.left)
   }
}

In-order traversal

The following is what a tree's mid-order traversal looks like:

left node -> root node -> right node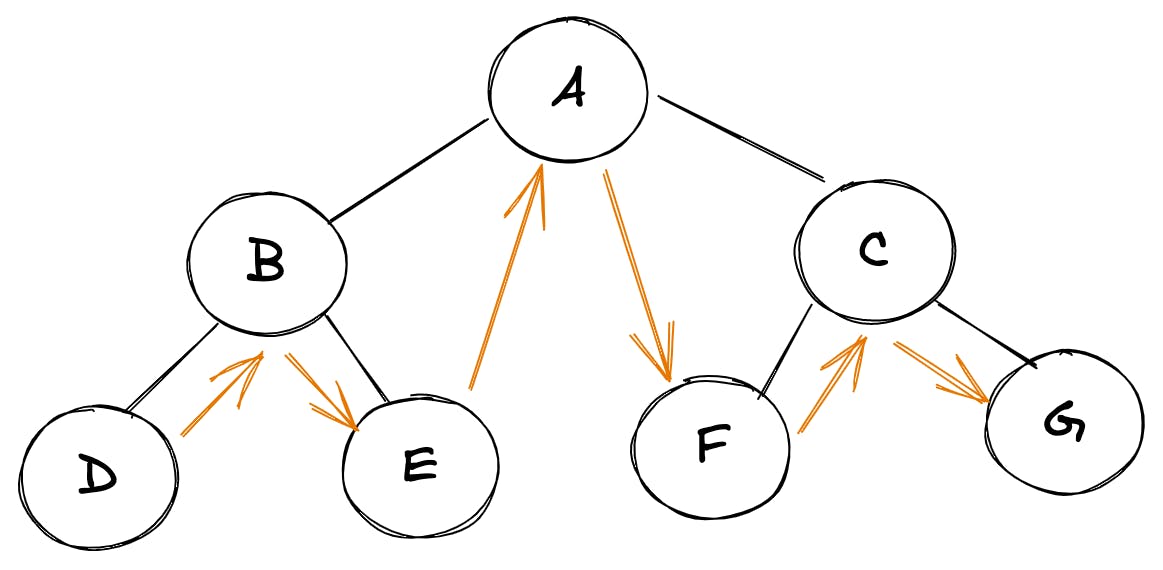

The trick:
We can use this simple technique to manually find the in-order traversal of any tree: place a plane mirror horizontally at the bottom of the tree and project all nodes.

accomplish:

Recursion:

function walkInOrder(root){
  if(root === null) return

  if(root.left) walkInOrder(root.left)

 // do something here
  console.log(root.val)

  if(root.right) walkInOrder(root.right)
}

Iteration: This algorithm may seem a bit mysterious at first. But it is quite intuitive. Let's look at it this way: In an in-order traversal, the leftmost child node is printed first, then the root node, and then the right node. So our first thought is:

const curr = root

while(curr){
  while(curr.left){
    curr = curr.left // get to leftmost child
  }

  console.log(curr) // print it

  curr = curr.right // now move to right child
}

In the above method, we cannot backtrack, that is, return to the parent node of the leftmost node, so we need a stack to record them. Therefore, our revised method may look as follows:

const stack = []
const curr = root

while(stack.length || curr){
  while(curr){
    stack.push(curr) // keep recording the trail, to backtrack
    curr = curr.left // get to leftmost child
  }
  const leftMost = stack.pop()
  console.log(leftMost) // print it

  curr = leftMost.right // now move to right child
}

Now we can use the above method to formulate the final iterative algorithm:

function walkInOrder(root){
  if(root === null) return

  const stack = []
  let current = root

  while(stack.length || current){
      while(current){
         stack.push(current)
         current = current.left
      }
      const last = stack.pop()

      // do something
      console.log(last)

      current = last.right
   }
}

Post-order traversal

The following is what a post-order traversal of a tree looks like:

 left node -> right node -> root node

The trick:

For fast manual post-order traversal of any tree: extract all the leftmost leaf nodes one by one.

accomplish:

Let us delve into the actual implementation of this traversal.

Recursion:

function walkPostOrder(root){
  if(root === null) return

  if(root.left) walkPostOrder(root.left)
  if(root.right) walkPostOrder(root.right)

  // do something here
  console.log(root.val)

}

Iteration: We already have an iterative algorithm for pre-order traversal. Can we use that? Since the post-order traversal seems to be the reverse order of the pre-order traversal. let's see:

// PreOrder:
root -> left -> right

// Reverse of PreOrder:
right -> left -> root

// But PostOrder is:
left -> right -> root

There is a subtle difference here. But we can slightly modify the pre-order algorithm, and then reverse the order to get the post-order result. The overall algorithm is as follows:

// record result using 
root -> right -> left

// reverse result
left -> right -> root

• Use a method similar to the iterative preorder algorithm above, using a temporary stack.

  • The only exception is that we use root-> right-> left instead of root-> left-> right
• Record the traversal sequence in an array result
• The reverse order of the result gives the post-order traversal

function walkPostOrder(root){
  if(root === null) return []

  const tempStack = [root], result = []

  while(tempStack.length){
      const last = tempStack.pop()

      result.push(last)

      if(last.left) tempStack.push(last.left)
      if(last.right) tempStack.push(last.right)
    }

    return result.reverse()
}

Extra: JavaScript prompt

What if we could traverse the tree in the following way:

 for(let node of walkPreOrder(tree) ){
   console.log(node)
 }

It looks really good, and it’s easy to read, doesn’t it? All we have to do is use a walk function, which returns an iterator.

Here is how we can modify the above walkPreOrder function to run according to the example shared above:

function* walkPreOrder(root){
   if(root === null) return

  const stack = [root]
  while(stack.length){
      const item = stack.pop()
      yield item
      if(item.right) stack.push(item.right)
      if(item.left) stack.push(item.left)
   }
}

Recommended reason

This article (with multiple pictures) introduces how to traverse the tree structure in the JavaScript language. It is written in a simple and easy-to-understand manner. It explains the realization of various methods such as breadth first and depth first. Translations will inevitably differ. Welcome to correct!

Original: https://stackfull.dev/tree-data-structure-in-javascript

Wonderful in the past

Generate an infinite level tree without recursion

based on qiankun micro front end actual deployment