公众号:DS数说
作者:xihuishaw
ARMA
AR(p),MA(q)二者相结合,即为ARMA(p,q),自回归移动平均。
公式表示:
当前时间步长的值是一个常数加上自回归滞后及其乘数之和,加上移动平均滞后及其乘数之和,再加上一些白噪声。
兼具捕捉滞后项及残差的影响,更具普遍性。确定p,q的阶,根据最小二乘或极大似然估计等非参数估计更新方程系数。
回顾一下时间序列建模流程:
- 平稳性检验:
- 判断序列是否平稳
如果不平稳,则需对序列进行变换(一般用差分); - 判断平稳序列是否为白噪音
<u>如平稳序列为白噪音,则不满足建模条件</u>
- 模型估计:
- 判断p,q的值
由历史的文章得知,可通过自相关系数(ACF)及偏自相关系数(PACF)决定,AR(p)出现p阶截尾,MA(q)出现q阶截尾 ; - 信息准则
如果ACF与PACF图看不出来明确的截尾,则采用信息准则进行判断,一般采用BIC、AIC - 二者相结合
- 模型残差检验
- 残差是否是平均值为0且方差为常数的正态分布(正态性)
- 检验残差的相关性(相关性)
ARIMA
自回归综合移动平均(ARIMA),和ARMA的差别,就是多了一个非平稳序列转化为平稳的参数d ,表示d阶差分后转化为平稳序列。ARIMA 模型只是差分时间序列上的 ARMA 模型。
ARIMA模型用符号ARIMA(p, d, q) 表示。
比如说ARIMA(1,1,0) 模型,(1,1,0) 意味着有一个自回归滞后,对数据进行了一次差分,并且没有移动平均项。
- p
模型的自回归部分,将过去值的影响纳入模型,也就是历史取值对未来有影响; - d是模型的集成部分。
使时间序列平稳所需的差分数 。比如说,如果过去三天的温度差异非常小,明天的温度可能和前几天温度差不多; - q
模型的移动平均部分,模型误差可以是过去时间点观察的误差值的线性组合。
SARIMA
SARIMA(Seasonal AutoRegressive Integrated Moving Average Model),具有外生回归模型的季节性自回归移动平均模型,简称季节性ARIMA。也就是在ARIMA的基础上,加入了季节性部分。季节性是指数据中具有固定频率的重复模式:每天、每两周、每四个月等重复的模式。
SARIMA模型可表示为SARIMA(p,d,q)x(P,D,Q)s,该式子满足乘法原则,前半部分表示非季节部分,后面表示季节部分,s表示季节性频率。
季节性成分可能捕捉长期模式,而非季节性成分调整了对短期变化的预测。
SARIMA实战
先依次把时间序列分析的建模流程一个个过一下。
1. 序列平稳性检验
这里采用单位根检验。
单位根检验:
对时间序列单位根的检验就是对时间序列平稳性的检验,非平稳时间序列如果存在单位根,则一般可以通过差分的方法来消除单位根,得到平稳序列。
单位根T检验:
- 原假设:有单位根
- p<显著性水平,则拒绝原假设,说明单位根平稳
def test_stationarity(timeseries,
maxlag=None, regression=None, autolag=None,
window=None, plot=False, verbose=False):
'''
单位根检验
'''
# set defaults (from function page)
if regression is None:
regression = 'c'
if verbose:
print('Running Augmented Dickey-Fuller test with paramters:')
print('maxlag: {}'.format(maxlag))
print('regression: {}'.format(regression))
print('autolag: {}'.format(autolag))
if plot:
if window is None:
window = 4
#Determing rolling statistics
rolmean = timeseries.rolling(window=window, center=False).mean()
rolstd = timeseries.rolling(window=window, center=False).std()
#Plot rolling statistics:
orig = plt.plot(timeseries, color='blue', label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean ({})'.format(window))
std = plt.plot(rolstd, color='black', label='Rolling Std ({})'.format(window))
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
#Perform Augmented Dickey-Fuller test:
dftest = smt.adfuller(timeseries, maxlag=maxlag, regression=regression, autolag=autolag)
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic',
'p-value',
'#Lags Used',
'Number of Observations Used',
])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
if verbose:
print('Results of Augmented Dickey-Fuller Test:')
print(dfoutput)
return dfoutput
2、acf、pacf图
画出原序列图、ACF及PACF图,大致判断序列的历史数据走势及p,q阶数
def tsplot(y, lags=None, title='', figsize=(14, 8)):
fig = plt.figure(figsize=figsize)
layout = (2, 2)
ts_ax = plt.subplot2grid(layout, (0, 0))
hist_ax = plt.subplot2grid(layout, (0, 1))
acf_ax = plt.subplot2grid(layout, (1, 0))
pacf_ax = plt.subplot2grid(layout, (1, 1))
y.plot(ax=ts_ax)
ts_ax.set_title(title)
y.plot(ax=hist_ax, kind='hist', bins=25)
hist_ax.set_title('Histogram')
smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
[ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
sns.despine()
fig.tight_layout()
return ts_ax, acf_ax, pacf_ax3、模型残差统计
检验标准化残差的正态性(Jarque-Bera 正态性检验):
- 原假设:是正态的
- p>alpha,接受原假设,残差是正态的
检验残差序列相关性(Ljung-Box 检验):
- 原假设:没有序列相关性
- p>alpha ,接受原假设,残差序列没有相关性
检验残差序列相关性(Durbin-Watson检验):
- 该统计量值越接近 2 越好,一般在 1~3 之间说明没问题;
- 小于 1 这说明残差存在自相关性。
def model_resid_stats(model_results,
het_method='breakvar',
norm_method='jarquebera',
sercor_method='ljungbox',
verbose=True,
):
(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
# Jarque-Bera 正态性检验
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]
# Ljung-Box检验 相关性检验
sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # last number for the largest lag
sercor_p = sercor_p[-1] # last number for the largest lag
# Durbin-Watson检验 相关性检验
dw_stat = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])
# check whether roots are outside the unit circle (we want them to be);
# will be True when AR is not used (i.e., AR order = 0)
arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
# will be True when MA is not used (i.e., MA order = 0)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)
if verbose:
print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw_stat))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))
stat = {'het_method': het_method,
'het_stat': het_stat,
'het_p': het_p,
'norm_method': norm_method,
'norm_stat': norm_stat,
'norm_p': norm_p,
'skew': skew,
'kurtosis': kurtosis,
'sercor_method': sercor_method,
'sercor_stat': sercor_stat,
'sercor_p': sercor_p,
'dw_stat': dw_stat,
'arroots_outside_unit_circle': arroots_outside_unit_circle,
'maroots_outside_unit_circle': maroots_outside_unit_circle,
}
return stat4、模型参数网格搜索
SARIMA模型的参数有6个,如果人工去选择的话,就得调秃头,所以得上网格搜索调一下,其实也可以用贝叶斯估计调参,这里只介绍网格。
这里主要关注SARIMAX这个函数的调用及其参数的含义。
- order:ARIMA对应的(p,d,q)
- seasonal_order: (P,D,Q,s)
def model_gridsearch(ts,
p_min,
d_min,
q_min,
p_max,
d_max,
q_max,
sP_min,
sD_min,
sQ_min,
sP_max,
sD_max,
sQ_max,
trends,
s=None,
enforce_stationarity=True,
enforce_invertibility=True,
simple_differencing=False,
plot_diagnostics=False,
verbose=False,
filter_warnings=True,
):
'''Run grid search of SARIMAX models and save results.
'''
cols = ['p', 'd', 'q', 'sP', 'sD', 'sQ', 's', 'trend',
'enforce_stationarity', 'enforce_invertibility', 'simple_differencing',
'aic', 'bic',
'het_p', 'norm_p', 'sercor_p', 'dw_stat',
'arroots_gt_1', 'maroots_gt_1',
'datetime_run']
# Initialize a DataFrame to store the results
df_results = pd.DataFrame(columns=cols)
mod_num=0
for trend,p,d,q,sP,sD,sQ in itertools.product(trends,
range(p_min,p_max+1),
range(d_min,d_max+1),
range(q_min,q_max+1),
range(sP_min,sP_max+1),
range(sD_min,sD_max+1),
range(sQ_min,sQ_max+1),
):
# initialize to store results for this parameter set
this_model = pd.DataFrame(index=[mod_num], columns=cols)
if p==0 and d==0 and q==0:
continue
try:
model = sm.tsa.SARIMAX(ts,
trend=trend,
order=(p, d, q),
seasonal_order=(sP, sD, sQ, s),
enforce_stationarity=enforce_stationarity,
enforce_invertibility=enforce_invertibility,
simple_differencing=simple_differencing,
)
if filter_warnings is True:
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
model_results = model.fit(disp=0)
else:
model_results = model.fit()
if verbose:
print(model_results.summary())
if plot_diagnostics:
model_results.plot_diagnostics();
stat = model_resid_stats(model_results,
verbose=verbose)
this_model.loc[mod_num, 'p'] = p
this_model.loc[mod_num, 'd'] = d
this_model.loc[mod_num, 'q'] = q
this_model.loc[mod_num, 'sP'] = sP
this_model.loc[mod_num, 'sD'] = sD
this_model.loc[mod_num, 'sQ'] = sQ
this_model.loc[mod_num, 's'] = s
this_model.loc[mod_num, 'trend'] = trend
this_model.loc[mod_num, 'enforce_stationarity'] = enforce_stationarity
this_model.loc[mod_num, 'enforce_invertibility'] = enforce_invertibility
this_model.loc[mod_num, 'simple_differencing'] = simple_differencing
this_model.loc[mod_num, 'aic'] = model_results.aic
this_model.loc[mod_num, 'bic'] = model_results.bic
# this_model.loc[mod_num, 'het_method'] = stat['het_method']
# this_model.loc[mod_num, 'het_stat'] = stat['het_stat']
this_model.loc[mod_num, 'het_p'] = stat['het_p']
# this_model.loc[mod_num, 'norm_method'] = stat['norm_method']
# this_model.loc[mod_num, 'norm_stat'] = stat['norm_stat']
this_model.loc[mod_num, 'norm_p'] = stat['norm_p']
# this_model.loc[mod_num, 'skew'] = stat['skew']
# this_model.loc[mod_num, 'kurtosis'] = stat['kurtosis']
# this_model.loc[mod_num, 'sercor_method'] = stat['sercor_method']
# this_model.loc[mod_num, 'sercor_stat'] = stat['sercor_stat']
this_model.loc[mod_num, 'sercor_p'] = stat['sercor_p']
this_model.loc[mod_num, 'dw_stat'] = stat['dw_stat']
this_model.loc[mod_num, 'arroots_gt_1'] = stat['arroots_outside_unit_circle']
this_model.loc[mod_num, 'maroots_gt_1'] = stat['maroots_outside_unit_circle']
this_model.loc[mod_num, 'datetime_run'] = pd.to_datetime('today').strftime('%Y-%m-%d %H:%M:%S')
df_results = df_results.append(this_model)
mod_num+=1
except:
continue
return df_results
5、搭建模型
5.1 导入数据
这里拆分测试集、验证集,不同于机器学习建模采取随机抽样的形式,因为时序数据是有序的。
liquor = pd.read_csv('liquor.csv', header=0, index_col=0, parse_dates=[0])
n_sample = liquor.shape[0]
n_train=int(0.95*n_sample)+1
n_forecast=n_sample-n_train
# 拆分测试集序列和验证集序列
liquor_train = liquor.iloc[:n_train]['Value']
liquor_test = liquor.iloc[n_train:]['Value']
print(liquor_train.shape)
print(liquor_test.shape)
print("Training Series:", "\n", liquor_train.tail(), "\n")
print("Testing Series:", "\n", liquor_test.head())
5.2 可视化原序列、acf及pacf
tsplot(liquor_train, title='Liquor Sales (in millions of dollars)', lags=40);从原始序列图发现,序列并不是平稳序列,并且从acf、pacf图中,没有明显的截尾,没办法判断p,q。
5.3 非平稳序列转平稳序列
# 检验平稳性
test_stationarity(liquor_train)单位根检验,p>0.05,不能拒绝原假设(有单位根),序列非平稳。
# 差分
test_stationarity(liquor_train.diff().dropna())一阶差分,p<0.05,拒绝原假设,序列平稳,所以该序列进行一阶差分就够了。
5.4 模型参数网格搜索
p_min = 0
d_min = 0
q_min = 0
p_max = 2
d_max = 1
q_max = 2
sP_min = 0
sD_min = 0
sQ_min = 0
sP_max = 1
sD_max = 1
sQ_max = 1
# 以一年为一个周期
s=12
# trends=['n', 'c']
trends=['n']
enforce_stationarity=True
enforce_invertibility=True
simple_differencing=False
plot_diagnostics=False
verbose=False
df_results = model_gridsearch(liquor['Value'],
p_min,
d_min,
q_min,
p_max,
d_max,
q_max,
sP_min,
sD_min,
sQ_min,
sP_max,
sD_max,
sQ_max,
trends,
s=s,
enforce_stationarity=enforce_stationarity,
enforce_invertibility=enforce_invertibility,
simple_differencing=simple_differencing,
plot_diagnostics=plot_diagnostics,
verbose=verbose,
)
5.5 模型选择与搭建
df_results.sort_values(by='bic').head(10)这里选择BIC作为模型评估指标,选择最小的BIC对应的参数进行建模,即(p,d,q)=(2,1,0),(P,D,Q)s = (0,1,1)12。
将上述最优参数代入模型中:
mod = sm.tsa.statespace.SARIMAX(liquor_train, order=(2,1,0), seasonal_order=(0,1,1,12))
sarima_fit2 = mod.fit()
print(sarima_fit2.summary())
来看看得到的训练集模型的统计量:
- coef :回归的系数
- p>|z|:系数是否显著
- JB:残差的正态检验
- LB:残差序列的相关性检验
模型残差的可视化检验:
- 随机性:是否为白噪音
- 正态性:是否为正态分布
- 相关性:残差之间相关性是否较低
满足以上条件,模型的建立才算成功。
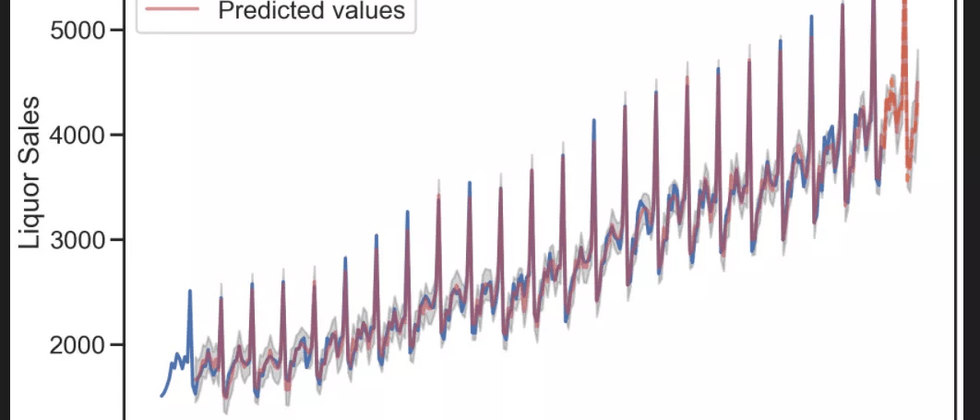
sarima_fit2.plot_diagnostics(figsize=(16, 12));5.6 预测
fig, ax1 = plt.subplots(nrows=1, ncols=1, figsize=(12, 8))
ax1.plot(liquor_train, label='In-sample data', linestyle='-')
# subtract 1 only to connect it to previous point in the graph
ax1.plot(liquor_test, label='Held-out data', linestyle='--')
# yes DatetimeIndex
pred_begin = liquor_train.index[sarima_fit2.loglikelihood_burn]
pred_end = liquor_test.index[-1]
pred = sarima_fit2.get_prediction(start=pred_begin.strftime('%Y-%m-%d'),
end=pred_end.strftime('%Y-%m-%d'))
pred_mean = pred.predicted_mean
pred_ci = pred.conf_int(alpha=0.05)
ax1.plot(pred_mean, 'r', alpha=.6, label='Predicted values')
ax1.fill_between(pred_ci.index,
pred_ci.iloc[:, 0],
pred_ci.iloc[:, 1], color='k', alpha=.2)
ax1.set_xlabel("Year")
ax1.set_ylabel("Liquor Sales")
ax1.legend(loc='best');
fig.tight_layout();
放大看,拟合的效果是非常好的~(肉眼可见的稳)
参考链接:
- http://statsmodels.sourceforg...
- https://wiki.mbalib.com/wiki/...
- http://www.statsmodels.org/de...
- http://www.statsmodels.org/de...
- https://www.statsmodels.org/d...
- https://www.statsmodels.org/d...
- https://cloud.tencent.com/dev...
- https://blog.csdn.net/qifeide...
欢迎关注个人公众号:DS数说









**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。