堆和堆排序

大家好，我是周一。

今天我们聊聊堆，以及堆排序。

一、堆

谈到堆，首先我们要从二叉树说起，从二叉树到完全二叉树，再才到堆。

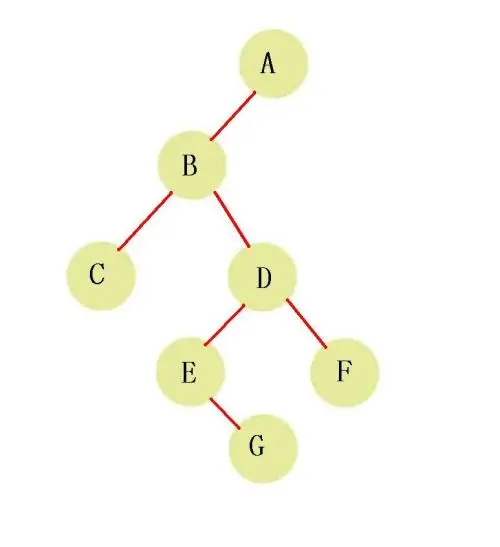
1、二叉树

每个结点最多只能有两棵子树，且有左右之分

2、完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中（除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树）编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

通俗的说法就是：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

对于某个位置为i的节点，左孩子（如果有）2i+1，右孩子（如果有）2i+2，父节点(i-1)/2（向下取整）

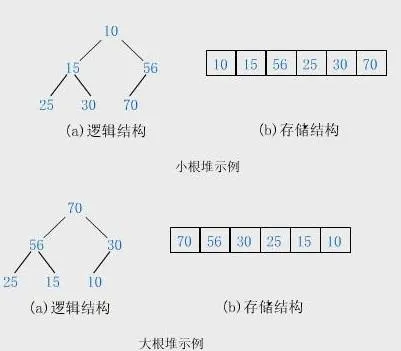
3、堆

首先是一个完全二叉树。同时区分大根堆和小根堆。

大根堆：每一颗子树的最大值都是头节点。

小根堆：每一颗子树的最小值都是头节点。

（1）对于用户依次输入数字的一个数组，如何将其构造为大根堆？

每插入一个数都和父节点比较，大于父节点则和父节点交换，直到根节点；如果小于父节点，则马上停止比较。

// 对于新加进来的i位置的数，请放到数组合适位置，使其成为一个大根堆
private void heapInsert(int[] arr, int i) {
    // i = 0 或 i位置数小于父节点
    // while包含这两种终止条件
    while(arr[i] > arr[(i - 1)/2]) {
        swap(arr, i, (i - 1)/2);
        i = (i - 1)/2;
    }
}

（2）获取当前数组最大值，并从堆中删除，同时维持大根堆结构

public int pop() {
    int ans = heap[0];
    swap(heap, 0, --heapSize);
    heapify(heap, 0, heapSize);
    return ans;
}

// 将index位置的数往下沉，直到较大的孩子都没自己大，或者没孩子了
private void heapify(int[] arr, int index, int heapSize) {
    // 左子树位置
    int left = 2 * index + 1;
    while(left < heapSize) {        
        // 找到左右子树哪个值更大
       int maxIndex = (left + 1) < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
       // 将左右子树中较大的和父节点比较
       maxIndex = arr[maxIndex] > arr[index] ? maxIndex : index;
       // 左右子树较大的值都小于父节点，停止循环     
       if (maxIndex == index) {
           break;
       }
       // 将左右子树中较大的和父节点交换
       swap(arr, maxIndex, index);
       // 当前比较的节点位置来到较大的子节点
       index = maxIndex;
       // 重新获取当前节点的左子树
       left = 2 * index + 1;
    }
}

4、PriorityQueue

底层就是用堆实现的，默认是小根堆

5、时间复杂度

heapinsert，在已经是堆结构的数中加入一个数，时间复杂度是O(logN)

heapify，在已经是堆结构的数中加入一个数，时间复杂度是O(logN)

二、堆排序

1、将整个数组调整为大根堆，那么此时0位置的数就是最大值

2、将0位置和数组最大位置的数交换，此时的最大值就处于最后排好序的位置了

3、数组的调整范围个数减一，循环执行1、2步，直到数组为空

public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    // 将整个数组调整为大根堆，O(NlogN)
    for (int i = 0; i < arr.length; i++) { // O(N)
        heapinsert(arr, i); // O(logN)
    }
    // 获取当前数组大小
    int heapSize = arr.length;
    // 0位置和数组最大位置的数交换
    swap(arr, 0, --heapSize);
    while(heapSize > 0) {
        // 将交换到0位置的数下沉，即将当前数组再次调整为大根堆
        heapify(arr, 0, heapSize);
        // 0位置和数组最大位置的数交换
        swap(arr, 0, --heapSize);
    }    
}

4、复杂度

（1）时间复杂度：O(N*logN)

（2）额外空间复杂度：O(1)